湖北省宜昌市五峰县达标名校2021-2022学年中考数学最后一模试卷含解析

这是一份湖北省宜昌市五峰县达标名校2021-2022学年中考数学最后一模试卷含解析，共18页。
2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．如果（，均为非零向量），那么下列结论错误的是（　　）
A．// B．-2=0 C．= D．
2．下列计算正确的是（　　）
A．（a）＝a B．a+a＝a
C．（3a）•（2a）＝6a D．3a﹣a＝3
3．下列二次根式中，是最简二次根式的是（　　）
A． B． C． D．
4．二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为( )

A． B． C． D．
5．若二次函数y=-x2+bx+c与x轴有两个交点（m，0），（m-6，0）,该函数图像向下平移n个单位长度时与x轴有且只有一个交点，则n的值是（ ）
A．3 B．6 C．9 D．36
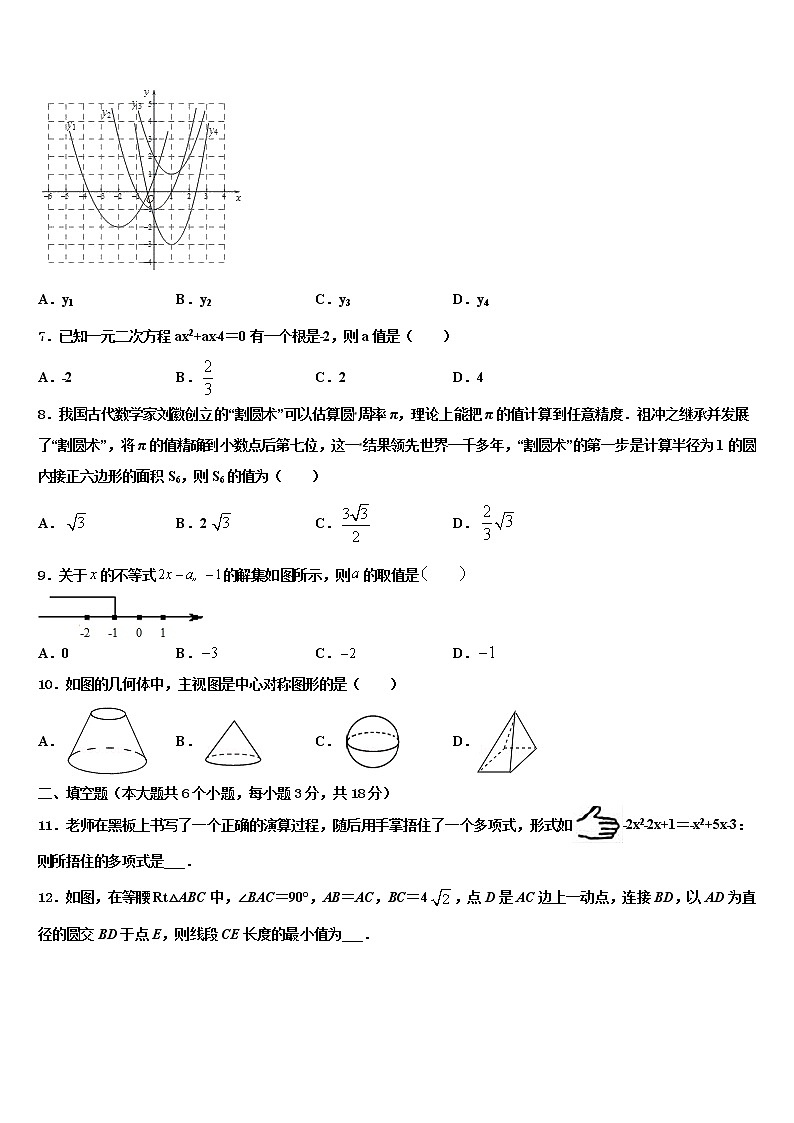
6．在平面直角坐标系xOy中，四条抛物线如图所示，其解析式中的二次项系数一定小于1的是（　　）

A．y1 B．y2 C．y3 D．y4
7．已知一元二次方程ax2+ax﹣4＝0有一个根是﹣2，则a值是（　　）
A．﹣2 B． C．2 D．4
8．我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度．祖冲之继承并发展了“割圆术”，将π的值精确到小数点后第七位，这一结果领先世界一千多年，“割圆术”的第一步是计算半径为1的圆内接正六边形的面积S6，则S6的值为（　　）
A． B．2 C． D．
9．关于的不等式的解集如图所示，则的取值是　　

A．0 B． C． D．
10．如图的几何体中，主视图是中心对称图形的是（　　）
A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如﹣2x2﹣2x+1＝﹣x2+5x﹣3：则所捂住的多项式是___．
12．如图，在等腰Rt△ABC中，∠BAC＝90°，AB＝AC，BC＝4，点D是AC边上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值为___．

13．若关于的不等式组无解， 则的取值范围是 ________.
14．按照一定规律排列依次为，…..按此规律，这列数中的第100个数是_____．
15．2018年春节期间，反季游成为出境游的热门，中国游客青睐的目的地仍主要集中在温暖的东南亚地区．据调查发现2018年春节期间出境游约有700万人，游客目的地分布情况的扇形图如图所示，从中可知出境游东南亚地区的游客约有________万人．

16．已知m、n是一元二次方程x2+4x﹣1＝0的两实数根，则＝_____．
三、解答题（共8题，共72分）
17．（8分）如图，在顶点为P的抛物线y=a（x-h）2+k（a≠0）的对称轴1的直线上取点A（h，k+），过A作BC⊥l交抛物线于B、C两点（B在C的左侧），点和点A关于点P对称，过A作直线m⊥l．又分别过点B，C作直线BE⊥m和CD⊥m，垂足为E，D．在这里，我们把点A叫此抛物线的焦点，BC叫此抛物线的直径，矩形BCDE叫此抛物线的焦点矩形．
（1）直接写出抛物线y=x2的焦点坐标以及直径的长．
（2）求抛物线y=x2-x+的焦点坐标以及直径的长．
（3）已知抛物线y=a（x-h）2+k（a≠0）的直径为，求a的值．
（4）①已知抛物线y=a（x-h）2+k（a≠0）的焦点矩形的面积为2，求a的值．
②直接写出抛物线y=x2-x+的焦点短形与抛物线y=x2-2mx+m2+1公共点个数分别是1个以及2个时m的值．

18．（8分）某中学为了考察九年级学生的中考体育测试成绩（满分30分），随机抽查了40名学生的成绩（单位：分），得到如下的统计图①和图②．请根据相关信息，解答下列问题：

（1）图中m的值为_______________.
（2）求这40个样本数据的平均数、众数和中位数：
（3）根据样本数据，估计该中学九年级2000名学生中，体育测试成绩得满分的大约有多少名学生。
19．（8分）计算：sin30°•tan60°+.．
20．（8分）如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．

21．（8分）某花卉基地种植了郁金香和玫瑰两种花卉共 30 亩，有关数据如表：

成本
（单位：万元/亩）
销售额
（单位：万元/亩）
郁金香
2.4
3
玫瑰
2
2.5
（1）设种植郁金香 x 亩，两种花卉总收益为 y 万元，求 y 关于 x 的函数关系式．（收益=销售额﹣成本）
（2） 若计划投入的成本的总额不超过 70 万元，要使获得的收益最大，基地应种植郁金香和玫瑰个多少亩？
22．（10分）如图，在△ABC中，∠ABC=90°，BD⊥AC，垂足为D，E为BC边上一动点（不与B、C重合），AE、BD交于点F．
（1）当AE平分∠BAC时，求证：∠BEF=∠BFE；
（2）当E运动到BC中点时，若BE=2，BD=2.4，AC=5，求AB的长．

23．（12分）先化简，再求值：，其中x＝－5
24．先化简：，然后从的范围内选取一个合适的整数作为x的值代入求值．



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、B
【解析】
试题解析：向量最后的差应该还是向量. 故错误.
故选B.
2、A
【解析】
根据同底数幂的乘法的性质，幂的乘方的性质，积的乘方的性质，合并同类项的法则，对各选项分析判断后利用排除法求解．
【详解】
A．（a2）3=a2×3=a6，故本选项正确；
B．a2+a2=2a2，故本选项错误；
C．（3a）•（2a）2=（3a）•（4a2）=12a1+2=12a3，故本选项错误；
D．3a﹣a=2a，故本选项错误．
故选A．
【点睛】
本题考查了合并同类项，同底数幂的乘法，幂的乘方，积的乘方和单项式乘法，理清指数的变化是解题的关键．
3、B
【解析】
根据最简二次根式必须满足两个条件：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式判断即可．
【详解】
A、 =4，不符合题意；
B、是最简二次根式，符合题意；
C、=，不符合题意；
D、=，不符合题意；
故选B．
【点睛】
本题考查最简二次根式的定义．最简二次根式必须满足两个条件：（1）被开方数不含分母；（2）被开方数不含能开得尽方的因数或因式．
4、D
【解析】
根据二次函数图象开口向上得到a>0，再根据对称轴确定出b，根据二次函数图形与轴的交点个数，判断的符号，根据图象发现当x=1时y=a+b+c0，
∵对称轴为直线
∴b0，
∵当x=1时y=a+b+c