初中数学第二章 二次函数4 二次函数的应用精品当堂达标检测题

这是一份初中数学第二章 二次函数4 二次函数的应用精品当堂达标检测题，文件包含答案docx、原卷docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
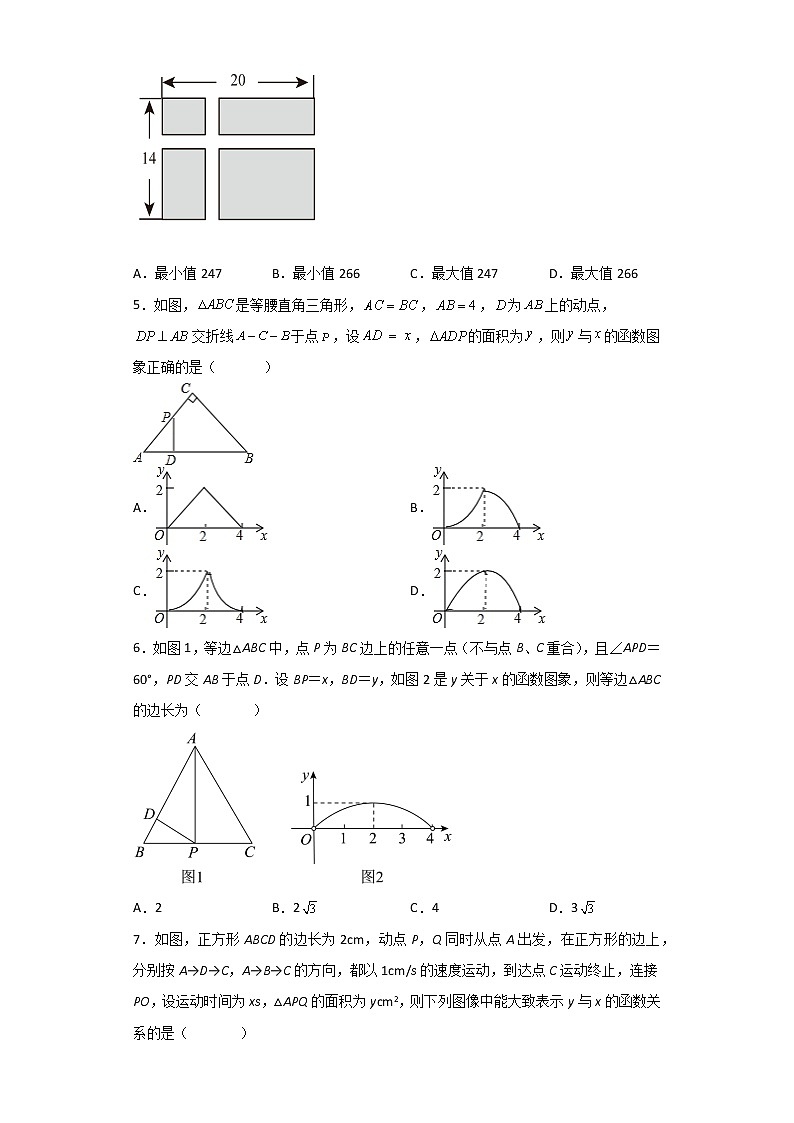
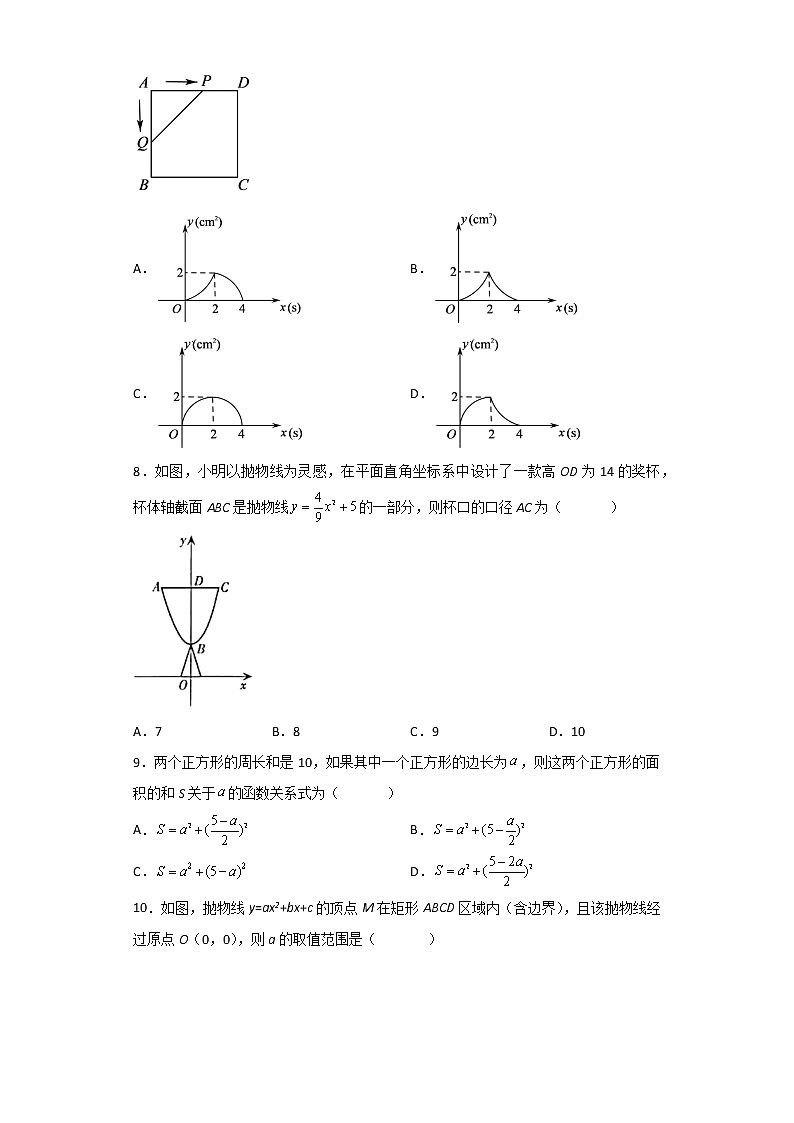
北师大版 九下  第2章 2.4（1）二次函数应用图形、拱桥、运动问题一，选择题（30分）1、．如图，用一段长为18米的篱笆围成一个一边靠墙（墙长不限）的矩形花园，设该矩形花园的一边长为，另一边的长为，矩形的面积为．当在一定范围内变化时，和都随的变化而变化，那么与．与满足的函数关系分别是（   ） A．一次函数关系，二次函数关系 B．反比例函数关系，二次函数关系C．一次函数关系，反比例函数关系 D．反比例函数关系，一次函数关系 2、如图是抛物线形的拱桥，当水面宽4m时，顶点离水面2m，当水面宽度增加到6m时，水面下降（　 　）A．1m B．1.5m C．2.5m D．2m3．如图，某拱形门建筑的形状时抛物线，拱形门地面上两点的跨度为192米，高度也为192米，若取拱形门地面上两点的连线作x轴，可用函数表示，则a的值为（    　）A． B． C． D．4．如图，在长为20m、宽为14m的矩形花圃里建有等宽的十字形小径，若小径的宽不超过1m，则花圃中的阴影部分的面积有（    ） A．最小值247 B．最小值266 C．最大值247 D．最大值2665．如图，是等腰直角三角形，，，为上的动点，交折线于点，设，的面积为，则与的函数图象正确的是（       ）A． B．C． D．6．如图1，等边△ABC中，点P为BC边上的任意一点（不与点B、C重合），且∠APD＝60°，PD交AB于点D．设BP＝x，BD＝y，如图2是y关于x的函数图象，则等边△ABC的边长为（         ）A．2 B．2 C．4 D．37．如图，正方形ABCD的边长为2cm，动点P，Q同时从点A出发，在正方形的边上，分别按A→D→C，A→B→C的方向，都以1cm/s的速度运动，到达点C运动终止，连接PO，设运动时间为xs，△APQ的面积为ycm2，则下列图像中能大致表示y与x的函数关系的是（        ）A． B．C． D．8．如图，小明以抛物线为灵感，在平面直角坐标系中设计了一款高OD为14的奖杯，杯体轴截面ABC是抛物线的一部分，则杯口的口径AC为（        ）A．7 B．8 C．9 D．109．两个正方形的周长和是10，如果其中一个正方形的边长为，则这两个正方形的面积的和S关于的函数关系式为（        ）A． B．C． D．10．如图，抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内（含边界），且该抛物线经过原点O（0，0），则a的取值范围是（        ）A．－2≤a≤－1 B． C． D．二、填空题(共24分)11．如图用一段长为16m的篱笆围成一个一边靠墙的矩形围栏（墙长9m），则这个围栏的最大面积为________ ．12．如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，以B为原点、AB所在水平线为x轴建立坐标系，拱桥对应抛物线的解析式为__________________．13．如图，在平面直角坐标系中，点A（4，8）在抛物线上，过点A作y轴的垂线，交抛物线于另一点B，点C、D在线段AB上，分别过点C、D作x轴的垂线交抛物线于E、F两点．当四边形CDFE为正方形时，线段CD的长为___________．14．如图，在一块等腰直角三角形ABC的铁皮上截取一块矩形铁皮，要求截得的矩形的边EF在的边BC上，顶点D、G分别在边AB、AC上．已知厘米，设DG的长为x厘米，矩形DEFG的面积为y平方厘米，那么y关于x的函数解析式为________________．（不要求写出定义域）15．如图，矩形中，，，点从点出发，沿边向点以1cm/s的速度移动；点从点出发，沿边向点以2cm/s的速度移动．，同时出发，分别到，后停止移动，则的最小面积是______．16、如图，正方形ABCD的边AB在x轴上，点A(-2，0)点B(1，0)，抛物线y=x2-4x+m与正方形有两个交点时，则m的取值范围是_______． 三、解答题：（66分）17.（6分）某公路有一个抛物线形状的隧道ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为y＝﹣x2+c且过顶点C（0，5）.（长度单位：m）(1)直接写出c＝　 　；(2)求该隧道截面的最大跨度（即AB的长度）是多少米？(3)该隧道为双向车道，现有一辆运货卡车高4米、宽3米，问这辆卡车能否顺利通过隧道？请说明理由.      18、（8分）如图1，是抛物线形的拱桥，当拱顶高水面2米时，水面宽4米．如图建立平面直角坐标系，解答下列问题： (1)如图2，求该抛物线的函数解析式．(2)当水面AB下降1米，到CD处时，水面宽度增加多少米？（保留根号）(3)当水面AB上升1米时，水面宽度减少多少米？（保留根号）   19、（8分）如图，一座温室实验室的横截面由抛物线和矩形组成，矩形的长是16m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=-x2+bx+c表示，CD为一排平行于地面的加湿管．(1)求抛物线的函数关系式，并计算出拱顶到地面的距离．(2)若加湿管的长度至少是12m，加湿管与拱顶的距离至少是多少米？(3)若在加湿管上方还要再安装一排恒温管(两排管道互相平行)，且恒温管与加湿管相距1.25m，恒温管的长度至少是多少米？
20、（10分）．如图，隧道的截面由抛物线和矩形构成，矩形的长为，宽为，以所在的直线为轴，线段的中垂线为轴，建立平面直角坐标系．轴是抛物线的对称轴，最高点到地面距离为4米．(1)求出抛物线的解析式．(2)在距离地面米高处，隧道的宽度是多少？(3)如果该隧道内设单行道（只能朝一个方向行驶），现有一辆货运卡车高3.6米，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论．    21、（10分）如图，在△ABC中，∠ABC＝90°，AB＝8cm，BC＝6cm，动点P，Q分别从点A，B同时开始移动（移动方向如图所示），点P的速度为2cm/s，点Q的速度为1cm/s，点P移动到B点后停止，点Q也随之停止运动，设P、Q从点A、B同时出发，运动时间为ts，四边形APQC的面积是S(1)试写出S与t之间的函数关系式，并确定自变量的取值范围；(2)若S是21cm2时，确定t值；(3)t为何值时，S有最大（或最小）值，求出这个最值．     22、（12分）某公司有一个抛物线形蔬菜大棚，将其截面放在如图所示的直角坐标系中，抛物线可以用函数y＝ax2+bx来表示．已知大棚在地面上的宽度OA为4米，距离O点1米处的棚高BC为米．(1)求该抛物线的解析式；(2)求蔬菜大棚离地面的最大高度是多少米？(3)为了扩大经营规模，公司决定将原来的蔬菜大棚进行改造，新建的大棚与原来大棚的形状保持不变，但使地面的宽度增加到6米．求身高为1.68米的工作人员在不弯腰的情况下，在大棚内横向活动的范围是多少米？
    23．（12分）如图，在Rt△ABC中，∠C＝90°，AC＝BC，AB＝4cm，线段AB上一动点D，以1cm/s的速度从点A出发向终点B运动．过点D作DE⊥AB，交折线AC－CB于点E，以DE为一边，在DE右侧作正方形DEFC．设运动时间为x（s）（0＜x＜4）．正方形DEFG与△ABC重叠部分面积为y（cm2）．(1)当x＝        s时，点F在BC上；(2)求y关于x的函数解析式，并写出自变量x的取值范围．