广东省肇庆市2022-2023学年九年级上学期第一次月考模拟数学试题

广东省肇庆市2022-2023学年九年级上学期第一次月考模拟数学试题

考试时间：120分钟 满分：120分

姓名：__________ 班级：__________考号：__________

注意事项：
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡

一、单选题(共10题；共30分)

1．（3分）在下列方程中，属于一元二次方程的是（　　） 

A． B． C． D．

2．（3分）对于二次函数y＝﹣（x﹣1）2+4的图象，下列说法正确的是（　　） 

A．开口向上

B．顶点坐标是（﹣1，4）

C．图象与y轴交点的坐标是（0，4）

D．函数有最大值4

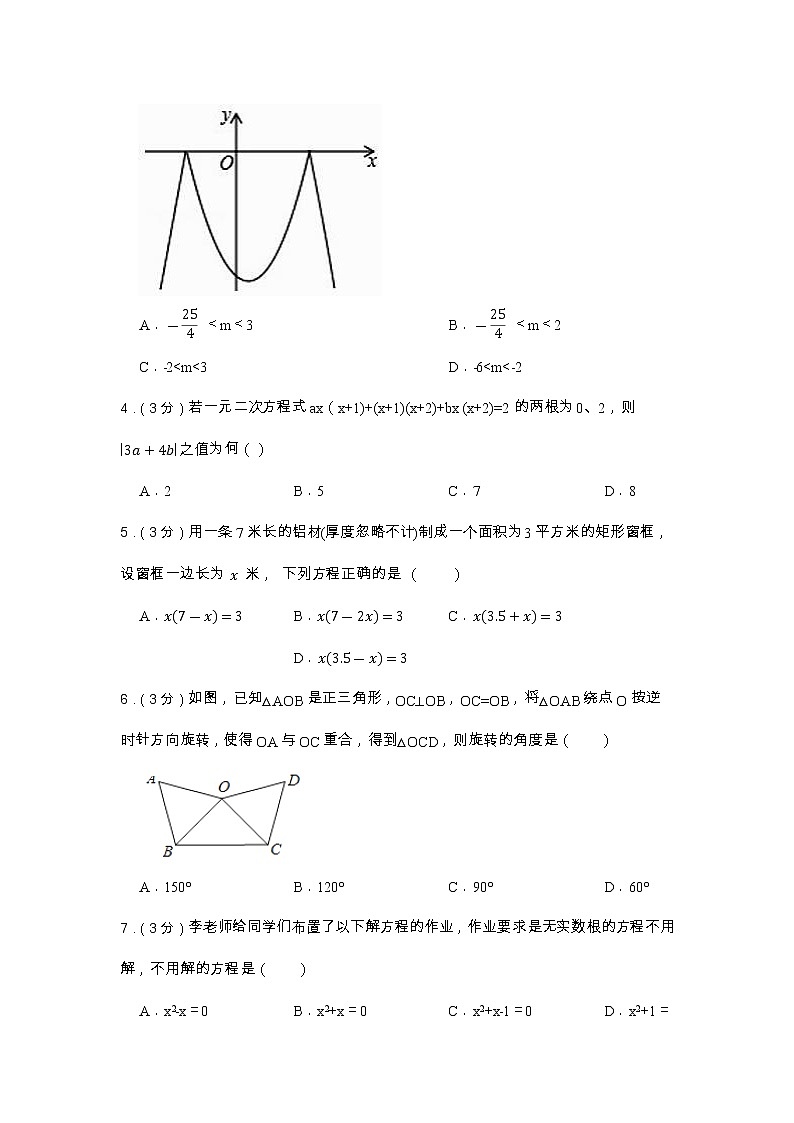
3．（3分）已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）

A． ＜m＜3 B． ＜m＜2

C．﹣2<m<3 D．﹣6<m<﹣2

4．（3分）若一元二次方程式ax（x+1)+(x+1)(x+2)+bx(x+2)=2的两根为0、2，则之值为何（）

A．2 B．5 C．7 D．8

5．（3分）用一条7米长的铝材(厚度忽略不计)制成一个面积为3平方米的矩形窗框，设窗框一边长为 米， 下列方程正确的是 （　　）  

A． B． C． D．

6．（3分）如图，已知△AOB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是（　　）

A．150° B．120° C．90° D．60°

7．（3分）李老师给同学们布置了以下解方程的作业，作业要求是无实数根的方程不用解，不用解的方程是（　　）  

A．x2﹣x＝0 B．x2+x＝0 C．x2+x﹣1＝0 D．x2+1＝0

8．（3分）二次函数y=ax2+c当x取x1 ，x2时，函数值相等，当x取x1+x2时，函数值为(　　)

A．a+c B．a-c C．-c D．c

9．（3分）函数y＝ 与y＝kx2﹣k（k≠0）在同一直角坐标系中的图象可能是（　　）  

A． B．

C． D．

10．（3分）已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，对称轴为直线 .下列结论中，正确的是（　　） 

A．abc>0 B．a+b=0 C．2b+c>0 D．4a+c<2b

二、填空题(共7题；共28分)

11．（4分）方程 中二次项是　     　，一次项系数是　     　．

12．（4分）在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图，自建房占地是边长为8m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG = 2BE. 如果设BE的长为x（单位：m），绿地AEFG的面积为y（单位：m2），那么y与x的函数的表达式为　                    　；当BE =　     　m时，绿地AEFG的面积最大.

13．（4分）抛物线y＝2(x＋3)(x－2)与x轴的交点坐标分别为 　                 　．

14．（4分）若关于x的一元二次方程(m+3)x2+5x+m2+2m-3=0有一个根为0，则m=　     　

15．（4分）已知a,b互为相反数，m，n互为倒数，则3(a+b)-2019mn的值为　     　．

16．（4分）如图，抛物线y＝ax2＋bx＋c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝﹣1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是﹣1≤x≤3；⑤当x＜0时，y随x增大而增大；其中结论正确的有　     　．

17．（4分）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数 （k≠0）的图象恰好经过点A′，B，则k的值为　     　

三、解答题(共8题；共62分)

18．（6分）用适当的方法解方程： 

（1）（3分）5x2﹣3x=x+1                       

（2）（3分）（x﹣4）2=（5﹣2x）2． 

19．（6分）已知，在平面直角坐标系中，A、B、C三点坐标分别为，A（4，4），B（﹣2，2），C（3，0）

（1）（3分）画出ΔABC关于原点成中心对称的中心对称图形△A1B1C1；

（2）（3分）写出A1、B1、C1三点的坐标．

20．（6分）《杨辉算法》中有这么一道题：“直田积八百六十四步，只云长阔共六十步，问长多几何？”意思是：一块矩形田地的面积为864平方步，只知道它的长与宽共60步，问它的长比宽多了多少步？  

21．（8分）关于x的一元二次方程 有实数根. 

（1）（4分）求k的取值范围；  

（2）（4分）若k是该方程的一个根，求 的值.  

22．（8分）某商场老板对一种新上市商品的销售情况进行记录，已知这种商品进价为每件 40 元，经过记录分析发现，当销售单价在 40 元至 90 元之间（含40 元和 90 元）时，每月的销售量 y（件）与销售单价 x（元）之间的关系可近似地看作一次函数，其图象如图所示．

（1）（3分）求y与x的函数关系式．  

（2）（3分）设商场老板每月获得的利润为P（元），求P与x之间的函数关系式；并求出利润的最大时销售单价为多少元？  

（3）（5分）如果想要每月获得 2400 元的利润，那么销售单价应定为多少元？  

23．（8分）如图，一单杆高2.2m，两立柱之间的距离为1.6m，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状． 

（1）（4分）一身高0.7m的小孩站在离立柱0.4m处，其头部刚好触上绳子，求绳子最低点到地面的距离； 

（2）（4分）为供孩子们打秋千，把绳子剪断后，中间系上一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳子正好各为2米，木板与地面平行，求这时木板到地面的距离．（供选用数据： ≈1.8， ≈1.9， ≈2.1） 

24．（10分）如图，在 中， ， ， ，点 沿 边从点 开始以 /秒的速度向点 移动，同时点 沿 边从点 开始以 /秒的速度向点 移动，用 表示移动的时间（ ）． 

（1）（5分）当 为何值时， 是等边三角形； 

（2）（5分）当 为何值时， 是直角三角形． 

25．（10分）设二次函数y＝x2﹣2（m+1）x+3﹣m，其中m是实数.

（1）（4分）若函数的图象经过点（﹣2，8），求此函数的表达式；

（2）（4分）若x＞0时，y随x的增大而增大，求m的最大值.

（3）（5分）已知A（﹣1，3），B（2，3），若该二次函数的图象与线段AB只有一个交点（不包括A，B两个端点），求m的取值范围.

答案解析部分

1．【答案】C

2．【答案】D

3．【答案】D

4．【答案】B

5．【答案】D

6．【答案】A

7．【答案】D

8．【答案】D

9．【答案】B

10．【答案】D

11．【答案】；

12．【答案】；2

13．【答案】(－3，0)，(2，0)

14．【答案】1

15．【答案】-2019

16．【答案】①②⑤

17．【答案】

18．【答案】（1）解：由原方程，得 

 5x2﹣4x﹣1=0，

因式分解，得

（5x+1）（x﹣1）=0

于是得5x+1=0或x﹣1=0，

则x1=﹣ ，x2=1

（2）解：由原方程，得 

（x﹣4）2﹣（5﹣2x）2=0，

（x﹣4﹣5+2x）（x﹣4+5﹣2x）=0，

即（3x﹣9）（1﹣x）=0，

解得x1=3，x2=1

19．【答案】（1）解：如图所示：

（2）解：A1（-4，-4），B1（2，-2），C1（-3，0）． 

20．【答案】解：设矩形的长为x步，则宽为（60﹣x）步， 

依题意得：x（60﹣x）＝864，

整理得：x2﹣60x+864＝0，

解得：x＝36或x＝24（不合题意，舍去），

∴60﹣x＝60﹣36＝24（步），

∴36﹣24＝12（步），

则该矩形的长比宽多12步

21．【答案】（1）解：∵ 有实数根，  

∴Δ≥0

即 .

∴k≤5

（2）解：∵k是方程 的一个根，  

∴

∴

=3

22．【答案】（1）解：设y与x的函数关系式为：y=kx+b（k≠0）， 

由题意得   ，解得

故 y=﹣4x+360（40≤x≤90）

（2）解：由题意得，p与x的函数关系式为： 

p=（x﹣40）（﹣4x+360）=﹣4x2+520x﹣14400，

∵x=﹣ =﹣   =65，

答：利润的最大时销售单价为 65 元

（3）解：当P=2400 时，﹣4x2+520x﹣14400=2400， 解得：x1 =60，x2=70， 

故销售单价应定为60元或70元．

23．【答案】（1）解：如图，建立直角坐标系，设二次函数为：y=ax2+c 

∵D（﹣0.4，0.7），B（0.8，2.2）

∴

∴

∴绳子最低点到地面的距离为0.2米

（2）解：分别作EG⊥AB于G，E、FH⊥AB于H， 

AG= （AB﹣EF）= （1.6﹣0.4）=0.6

在Rt△AGE中，AE=2，EG= ≈1.9

∴2.2﹣1.9=0.3（米）

∴木板到地面的距离约为0.3米

24．【答案】（1）解：由题意得：

中， ， ， ，

当 时， 为等边三角形，

即当运动时间为 时， 为等边三角形

（2）解：如图，当 时，

则 ，

如图，当 时，

同理可得：

综上：当运动时间为： 或 时， 为直角三角形.

25．【答案】（1）解：把点（﹣2，8）代入y＝x2﹣2（m+1）x+3﹣m，

得到，8＝4+4（m+1）+3﹣m，

m＝﹣1，

∴二次函数的解析式为y＝x2+4

（2）解：∵对称轴x＝﹣ ＝m+1，

又∵x＞0时，y随x的增大而增大，

∴m+1≤0，

∴m≤﹣1，

∴m的最大值为﹣1

（3）解：∵a＝1，

∴抛物线开口向上，

∵二次函数的图象与线段AB只有一个交点（不包括A，B两个端点），

∴满足条件： 或 ，

解得m＞0或m＜﹣3

 当抛物线的顶点在线段AB上时，
解得：(舍去）
综上所述，m＞0或m＜﹣3或