广东省深圳市2022届九年级下学期开学检测数学试卷(含答案)

这是一份广东省深圳市2022届九年级下学期开学检测数学试卷(含答案)，共13页。试卷主要包含了21×106等内容，欢迎下载使用。

1.某网店2021 年母亲节这天的营业额为221000 元，将数221000 用科学记数法表示为（ ）
A．2.21×106
B．2.21×105C．221×103D．0.221×106
2.已知 x1，x2 是一元二次方程 x2﹣2x＝0 的两个实数根，下列结论错误的是（ ）
1
A．x1≠x2B．x 2﹣2x1＝0C．x1+x2＝2D．x1•x2＝2
3.如图，已知△ABC，AB＜BC，用尺规作图的方法在 BC 上取一点 P，使得 PA+PC＝BC， 则下列选项正确的是（ ）
A． B．
C．D．
4.如图，正方形纸板的一条对角线垂直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板．在灯光照射下，正方形纸板在地面上形成的影子的形状可以是 （ ）
A． B． C． D．
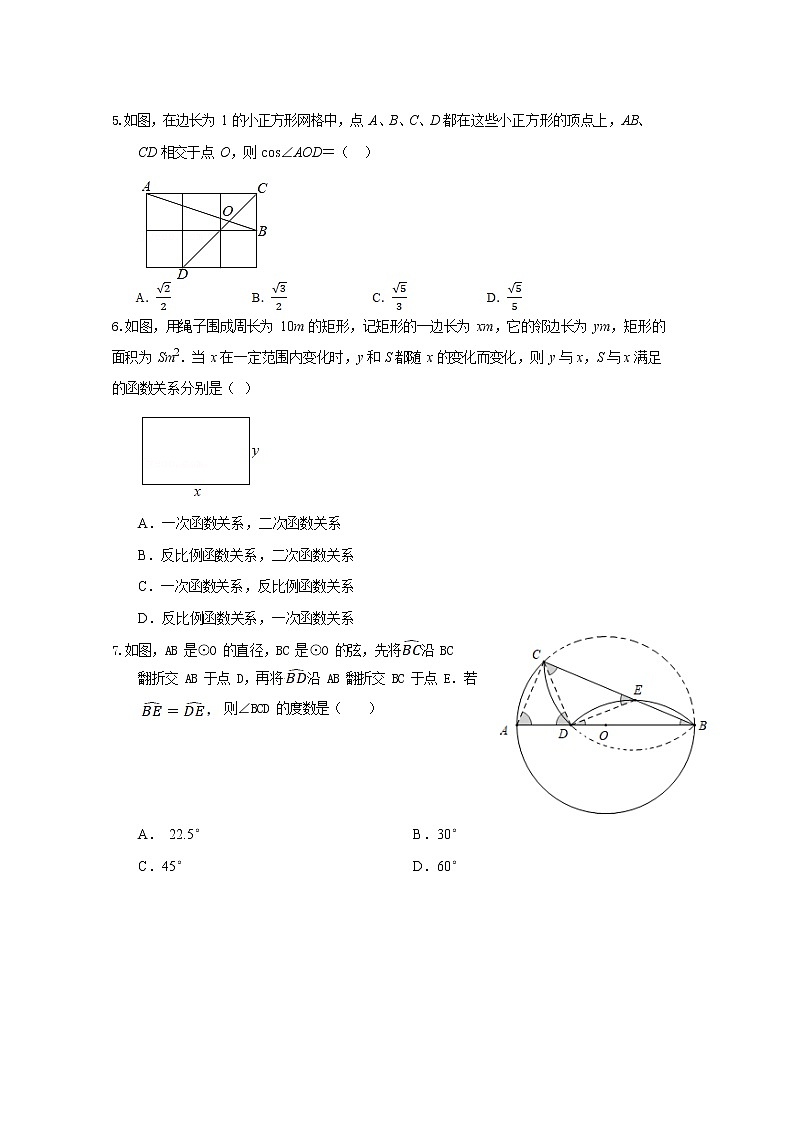
5.如图，在边长为 1 的小正方形网格中，点 A、B、C、D 都在这些小正方形的顶点上，AB、
CD 相交于点 O，则 cs∠AOD＝（ ）
6.如图，用绳子围成周长为 10m 的矩形，记矩形的一边长为 xm，它的邻边长为 ym，矩形的面积为 Sm2．当 x 在一定范围内变化时，y 和 S 都随 x 的变化而变化，则 y 与 x，S 与 x 满足的函数关系分别是（ ）
A．一次函数关系，二次函数关系B．反比例函数关系，二次函数关系C．一次函数关系，反比例函数关系D．反比例函数关系，一次函数关系
7.如图，AB 是⊙O 的直径，BC 是⊙O 的弦，先将 沿 BC
翻折交 AB 于点 D，再将 沿 AB 翻折交 BC 于点 E．若
则∠BCD 的度数是（ ）
A． 22.5°B．30°
C．45°D．60°
8.如图，在平面直角坐标系中，菱形 ABCD 的顶点 D 在第二象限，其余顶点都在第一象限，
AB∥x 轴，AO⊥AD，AO＝AD．过点 A 作 AE⊥CD，垂足为 E，DE＝4CE．反比例函数
的图象经过点 E，与边 AB 交于点 F，连接 OE，OF，EF．若
则 k 的值为（ ）

9.如图，抛物线 y＝ax2+bx+c 的对称轴是直线 x＝1，下列结论：
①abc＞0；②b2﹣4ac＞0；③8a+c＜0；④5a+b+2c＞0， 正确的有（ ）
A．4 个B．3 个C．2 个D．1 个
10.如图，在正方形 ABCD 中，点 E 是边 BC 的中点，连接 AE、DE，分别交 BD、AC 于点
P、Q，过点 P 作 PF⊥AE 交 CB 的延长线于 F，下列结论正确的有：（ ）
①AP＝FP， ③若四边形 OPEQ 的面积为 4，则该正方形 ABCD 的面积为
36，④CE•EF＝EQ•DE．
A．4 个B．3 个C．2 个D．1 个
二．填空题（共 5 小题，共 15 分）
11．已知一组数据 x1，x2，x3，x4 的方差是 2，则数据 x1+5，x2+5，x3+5，x4+5，的方差是 ．
12．因式分解：2x2y﹣8y3＝ ．
有一边长为 3 的等腰三角形，它的两边长是方程 x2﹣4x+k＝0 的两根，则 k＝ ．
如图，在半径 AC 为 2，圆心角为 90°的扇形内，以 BC 为直径作半圆，交弦 AB 于点
D，连接 CD，则图中阴影部分的面积是 ．
如图，正方形 ABCD 内接于⊙O，且AB=4 点 E 在?̂??上运动，连接 BE，作 AF⊥BE，垂足为 F，连接 CF．则 CF 长的最小值为 ．
三．解答题（共 7 小题）
16．（5 分）计算：

17．（5 分）先化简，再求值： 其中
18．（7 分）为迎接建党一百周年，我市计划用两种花卉对某广场进行美化．已知用 600 元购买 A 种花卉与用 900 元购买 B 种花卉的数量相等，且 B 种花卉每盆比 A 种花卉多 0.5 元．
A，B 两种花卉每盆各多少元？
（2）计划购买A，B两种花卉共6000盆，其中A种花卉的数量不超过B种花卉数量的13，
求购买 A 种花卉多少盆时，购买这批花卉总费用最低，最低费用是多少元？
19．（7 分）如图，在 Rt△ABC 中，∠C＝90°，AD 平分∠BAC 交 BC 于点 D，O 为 AB 上一点，经过点 A、D 的⊙O 分别交 AB、AC 于点 E、F．
求证：BC 是⊙O 的切线；
若 BE＝8，sinB= 求⊙O 的半径；
求证：AD2＝AB•AF．
20．（9 分）【问题情境】如图 1，在 Rt△ABC 中，∠ACB＝90°，CD⊥AB，垂足为 D，我们可以得到如下正确结论：①CD2＝AD•BD；②AC2＝AB•AD；③BC2＝AB•BD，这些结论是由古希腊著名数学家欧几里得在《几何原本》最先提出的，我们称之为“射影定理”，又称“欧几里德定理”．
请证明“射影定理”中的结论③BC2＝AB•BD．
【结论运用】
如图 2，正方形 ABCD 的边长为 6，点 O 是对角线 AC、BD 的交点，点 E 在 CD 上，过点 C 作 CF⊥BE，垂足为 F，连接 OF．
①求证：△BOF∽△BED．
②若 CE＝2，求 OF 的长．
21．（10 分）如图，点 B 是反比例函数 y= （x＞0）图象上一点，过点 B 分别向坐标轴作

垂线，垂足为 A，C．反比例函数 y= （x＞0）的图象经过 OB 的中点 M，与 AB，BC 分别

相交于点 D，E．连接 DE 并延长交 x 轴于点 F，点 G 与点 O 关于点 C 对称，连接 BF，BG．
（1）填空：k＝ ；
求△BDF 的面积；
求证：四边形 BDFG 为平行四边形．
22．（12 分）如图 1，已知抛物线 y＝ax2+bx+4 与 x 轴交于 A（﹣4，0），B（1，0）两点，与 y 轴交于点 C，顶点为 P．
抛物线的表达式是： ；顶点 P 的坐标为（ ， ）．
如 图 2，在抛物线的对称轴 l 上，有一条自由滑动的线段 EF（点 E 在点 F 的上方），已知 EF＝1，当|EC﹣BF|的值最大时，求四边形 EFBC 的面积．
如图 3，沿射线 AC 方向或其反方向平移抛物线 y＝ax2+bx+4，平移过程中 A，C 两
点的对应点分别记为 M，N，抛物线顶点 P 的对应点记为点 P'，在平移过程中，是否存在以 A，M，B 为顶点的三角形与△ABN 相似，若存在，请求出此时平移后的抛物线顶点P'的坐标；若不存在，请简要说明理由．答案
1-10 BDBCD ACABB
11. 2
12.
13. 3或4
14.
15.
16.

17.
18.
19.
20.
21.
22.