专题03运算能力课之整式综合运算重难点专练- 2022-2023学年七年级数学专题训练（浙教版）

专题03运算能力课之整式综合运算重难点专练（原卷版）

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．下列计算错误的是（    ）

A． B． C． D．

2．把四张形状大小完全相同的小长方形卡片（如图①），分两种不同形式不重叠的放在一个底面长为m，宽为n的长方形盒子底部（如图②、图③），盒子底面未被卡片覆盖的部分用阴影表示，设图②中阴影部分图形的周长为l1，图③中两个阴影部分图形的周长和为l2，若，则m，n满足（　　）

A．m＝n B．m＝n C．m＝n D．m＝n

3．数轴上，点对应的数是，点对应的数是，点对应的数是0.动点、从、同时出发，分别以每秒3个单位和每秒1个单位的速度向右运动．在运动过程中，下列数量关系一定成立的是（    ）

A． B． C． D．

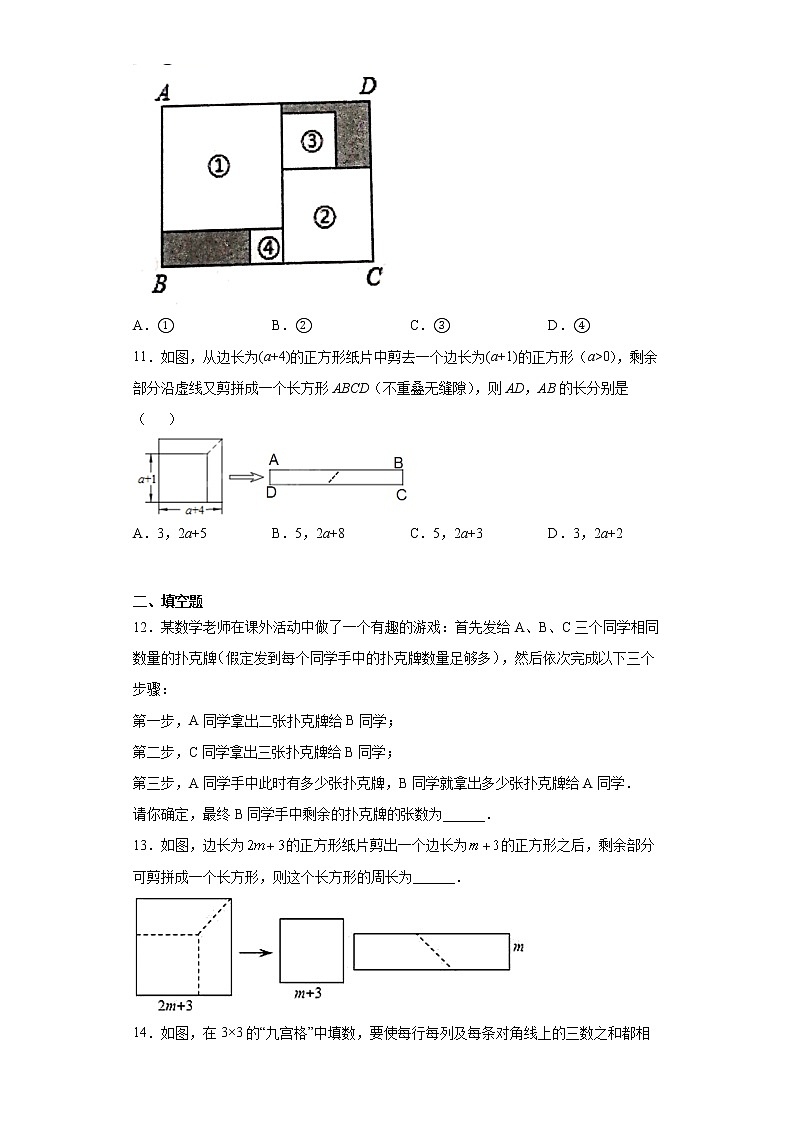
4．如图，两个长方形的面积分别为20，6，两阴影部分的面积分别为a，b，且，则等于（　　　）

A．6 B．7 C．14 D．16

5．如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中①，②两张正方形纸片既不重叠也无空隙．已知①号正方形边长为a，②号正方形边长为b，则阴影部分的周长是（　　　）

A． B． C． D．

6．下列各式的计算，正确的是（　　　）

A． B． C． D．

7．某水果商店在甲批发市场以每千克元的价格购进30千克的橘子，又在乙批发市场以每千克元（）的价格购进同样的50千克橘子．如果以每千克元的价格全部卖出这种橘子，那么这家商店（    ）

A．盈利了 B．亏损了 C．不盈不亏 D．盈亏不能确定

8．将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（    ）

A．16 B．24 C．30 D．40

9．下面是某同学在一次测试中的计算：

①；②；③；④，其中运算正确的个数为（    ）

A．4个 B．3个 C．2个 D．1个

10．将四张边长各不相同的正方形纸片按如图方式放入矩形内(相邻纸片之间互不重叠也无缝隙)，未被四张正方形纸片覆盖的部分用阴影表示．设右上角与左下角阴影部分的周长的差为．若知道的值，则不需测量就能知道周长的正方形的标号为（  ）

A．① B．② C．③ D．④

11．如图，从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形（a>0），剩余部分沿虚线又剪拼成一个长方形ABCD（不重叠无缝隙），则AD，AB的长分别是（   ）

A．3，2a+5 B．5，2a+8 C．5，2a+3 D．3，2a+2

二、填空题

12．某数学老师在课外活动中做了一个有趣的游戏：首先发给A、B、C三个同学相同数量的扑克牌假定发到每个同学手中的扑克牌数量足够多，然后依次完成以下三个步骤：

第一步，A同学拿出二张扑克牌给B同学；

第二步，C同学拿出三张扑克牌给B同学；

第三步，A同学手中此时有多少张扑克牌，B同学就拿出多少张扑克牌给A同学．

请你确定，最终B同学手中剩余的扑克牌的张数为______．

13．如图，边长为的正方形纸片剪出一个边长为的正方形之后，剩余部分可剪拼成一个长方形，则这个长方形的周长为______．

14．如图，在3×3的“九宫格”中填数，要使每行每列及每条对角线上的三数之和都相等．则B表示的数是________________.

15．已知矩形纸板的长和宽分别为和，按图中所示裁法做成两个无盖纸盒，则纸盒的长为_____．

三、解答题

16．数学课上，老师设计了一个数学游戏：若两个多项式相减的结果等于第三个多项式，则称这三个多项式为“友好多项式”．甲、乙、丙、丁四位同学各有一张多项式卡片，下面是甲、乙、丙、丁四位同学的对话：

请根据对话解答下列问题：

甲：我的多项式是2x2-3x-2

乙：我的多项式是3x2-x+1

丙：我的多项式是x2+2x+3

丁：我和甲、乙两位同学的多项式是友好多项式

（1）判断甲、乙、丙三位同学的多项式是否为“友好多项式”，并说明理由．

（2）丁的多项式是什么？（请直接写出所有答案）．

17．先化简，再求值：，其中，．

18．有长为米（米）的篱笆，利用它和房屋的一面墙（足够长）围成长方形园子，园子的宽为3米．

（1）若围成的园子如图1所示，求园子的面积（用含的代数式表示）．

（2）若围成的园子如图2所示，在园子的中间用篱笆隔开，并在上面开一道1米宽的门，此时园子的面积与图1中园子的面积相比，是增大还是减小了？增大或减小了多少？

19．化简求值：，其中，．

20．已知．

（1）化简

（2）当，时，求的值．

21．先化简，再求值：，其中，．

22．已知满足．

（1）求，的值．

（2）若，，求的值．

23．先化简，再求值：，其中，．

24．先化简，再求值：，其中，．

25．如图，点、在数轴上分别表示实数、，、两点之间的距离表示为，在数轴上、两点之间的距离请你利用数轴回答下列问题：

（1）数轴上表示2和6两点之间的距离是________，数轴上表示1和的两点之间的距离为________．

（2）数轴上表示和1两点之间的距离为_______，数轴上表示和两点之间的距离为________．

（3）若表示一个实数，且，化简________．

（4）的最小值为________．

（5）的最大值为________．

26．已知A、B为整式，A的表达式为3a2b﹣2ab2+abc，小明错将“C＝2A﹣B”看成“2A+B”，算得结果C＝4a2b﹣3ab2+4abc．

（1）求B的表达式；

（2）求正确的结果的表达式．

27．在3×3的方格中，每行、每列及对角线上的3个代数式的和都相等，我们把这样的方格图叫做“等和格”．如图的“等和格”中，每行、每列及对角线上的3个代数式的和都等于15.

（1）图1是显示部分代数式的“等和格”，可得a=_______（含b的代数式表示）；

（2）图2是显示部分代数式的“等和格”，可得a=__________,b=__________;

（3）图3是显示部分代数式的“等和格”，求b的值．（写出具体求解过程）

28．（1）已知代数式（kx2+6x+8）-（6x+5x2+2）化简后的结果是常数，求系数k的值.

（2）先化简，再求值：2（-3xy-y2）-（2x2-7xy-2y2），其中x=3，y=-.

29．某工厂第一车间有x人，第二车间比第一车间人数的 少30人，从第二车间调出y人到第一车间，那么：

（1）调动后，第一车间的人数为　   　人；第二车间的人数为　   　人．（用x，y的代数式表示）；

（2）求调动后，第一车间的人数比第二车间的人数多几人（用x，y的代数式表示）？

（3）如果第一车间从第二车间调入的人数，是原来调入的10倍，则第一车间人数将达到360人，求实际调动后，（2）题中的具体人数．

30．如果关于字母x的二次多项式－3x2＋mx＋nx2－x＋3的值与x的取值无关，求(m＋n)(m－n)的值．