



所属成套资源:2021-2022学年七年级数学下学期重难点精品讲义(沪教版)
第4讲-实数综合-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版)
展开这是一份第4讲-实数综合-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第4讲-实数综合解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第4讲-实数综合原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
第4讲-实数综合
1.理解分数指数幂的意义,能将方根与指数幂互化,能在简单运算中运用有理数指数幂的性质进行计算;
2.熟练运用有理数指数幂的性质进行计算,通过分数指数幂的学习,能进一步掌握乘方与开方的相关运算。
(以提问的形式回顾)
1. 分数指数幂
(其中、为整数,).
(其中、为整数,).
上面规定中的和叫做分数指数幂,是底数.
整数指数幂中运算法则在分数指数幂中也同样适用。
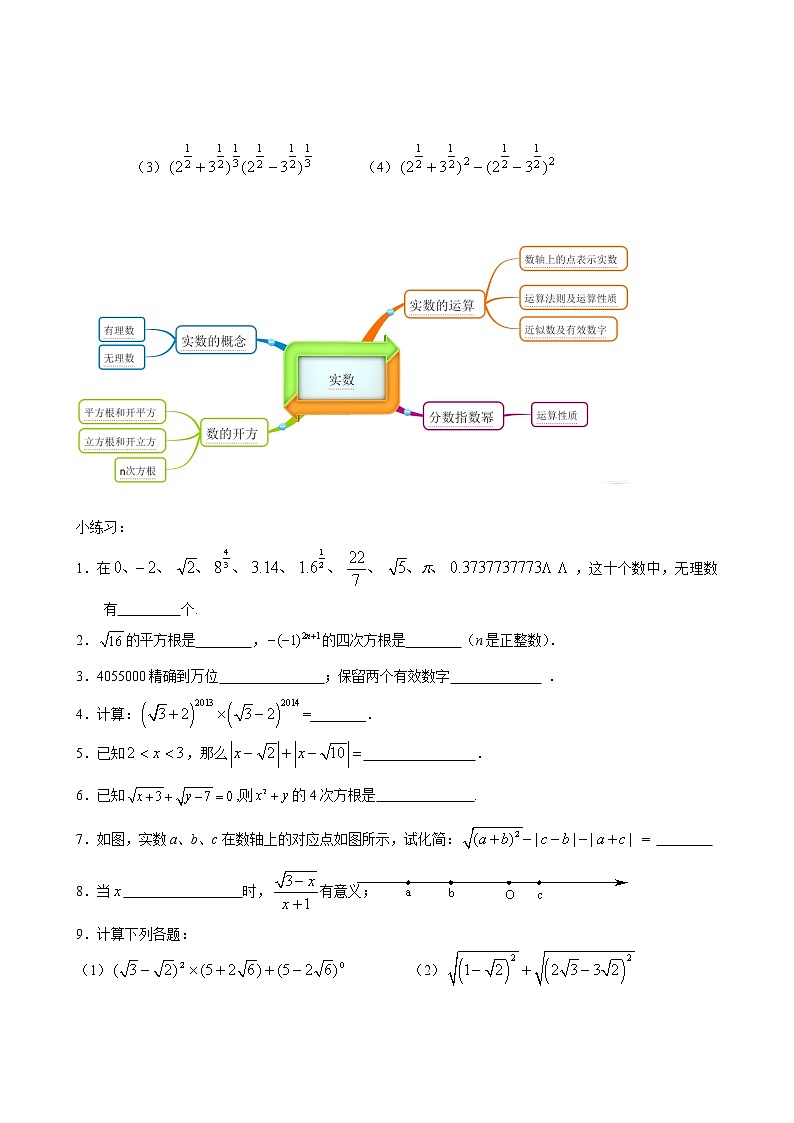
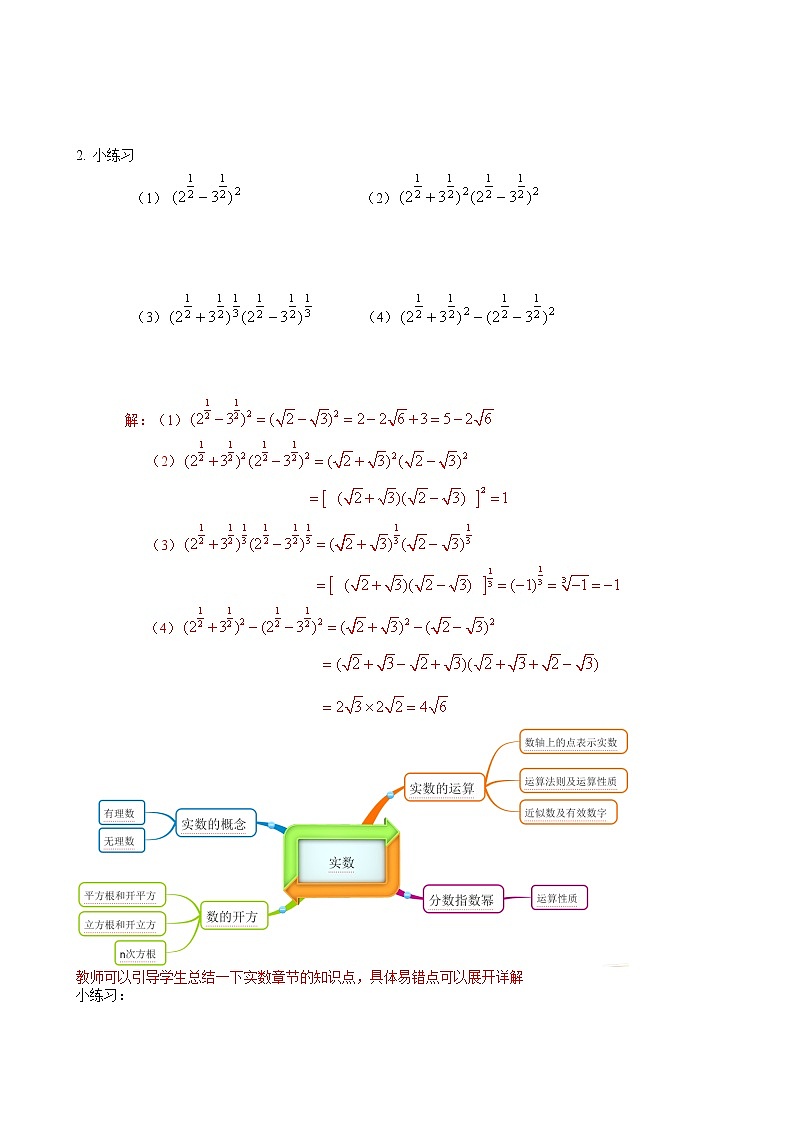
2. 小练习
(1) (2)
(3) (4)
解:(1)
(2)
(3)
(4)
教师可以引导学生总结一下实数章节的知识点,具体易错点可以展开详解
小练习:
1.在,这十个数中,无理数有 个.
2.的平方根是 ,的四次方根是 (n是正整数).
3.4055000精确到万位 ;保留两个有效数字 .
4.计算:=________.
5.已知,那么 .
6.已知,则的4次方根是 .
7.如图,实数a、b、c在数轴上的对应点如图所示,试化简: =
8.当 时,有意义;
9.计算下列各题:
(1) (2)
(3) (4)
10.设的小数部分为,的小数部分为,求的值。
参考答案:1、5; 2、;3、;4、;5、;
6、;7、0; 8、; 9、
10、
(采用教师引导,学生轮流回答的形式)
例1. 计算:
解:原式=
=
试一试:
解:原式=
=
=
例2. 解方程:
答案:
试一试:解方程:
答案:
例3. 已知、为整数,且满足,求的值。
解析:
(学生统一完成,互相批改,教师针对重难点详细讲解)
1.下列运算一定正确的是
A. B. C. D.
【答案】C
【分析】
直接利用二次根式的性质与化简以及积的乘方运算法则分别计算即可得出答案.
【详解】
A.=|a|,故此选项错误;
B.若=成立,则a,b均为非负数,故此选项错误;
C.a2•b2=(a•b)2,正确;
D.=(a≥0),故此选项错误.
故选C.
【点睛】
本题主要考查了二次根式的性质与化简以及积的乘方运算,正确掌握相关运算法则是解题的关键.
2.在、、、、、、…(它们的位数无限.相邻两个“1”之间“6”的个数依次增加1个)这些数中.无理数的个数是( )
A. B. C. D.
【答案】B
【分析】
根据题目中的数据,可以得到哪些数是无理数,本题得以解决.
【详解】
解:∵,
∴无理数是:、、、(它们的位数是无限的,相邻两个1之间6的个数依次增加1个),共4个.
故选.
【点睛】
本题考查算术平方根、分数指数幂、立方根、无理数,解答本题的关键是明确题意,找出题目中的无理数.
3.下列运算中,正确的是( )
A.; B.;
C.; D.;
【答案】D
【分析】
根据二次根式的加减运算法则、二次根式的性质、幂的运算性质和立方根的性质对各项进行分析判断即可得出答案.
【详解】
解:A项,,故本选项错误;
B项,,由于不知x的正负,故本选项错误;
C项,,故本选项错误;
D项,,正确;
故答案为D.
【点睛】
本题考查了幂的运算性质、二次根式的性质和运算、立方根的性质,熟知幂的运算性质、二次根式的性质和运算法则是解题的关键.
4.计算:______.
【答案】3
【分析】
利用分数指数幂化与根式的互化公式求解.
【详解】
解:,
故答案为:3.
【点睛】
本题主要考查了分数指数幂化与根式的互化,是基础题.
5.计算:_________.
【答案】4
【分析】
根据分数指数幂可得,再根据立方根计算.
【详解】
解:,
故答案为:4.
【点睛】
本题考查根式与分数指数幂的互化及其化简运算,基础题.
6.把表示成幂的形式___________.
【答案】
【分析】
根据分数指数幂即可求出答案.
【详解】
解:原式=,
故答案为:.
【点睛】
本题考查分数指数幂的公式,,其中a>0且a≠1.
7.计算:___________.
【答案】
【分析】
负分数指数运算规则为:,按照运算规则计算可得.
【详解】
故答案为:
【点睛】
本题考查负分数指数的计算,需要熟悉运算法则.
8.把写成方根的形式时是______.
【答案】
【分析】
根据分数指数幂公式= ,解答即可.
【详解】
解:根据分数指数幂公式=,
得=,
故答案为.
【点睛】
本题考查了分数指数幂,正确理解分数指数幂的含义是解题的关键.
9.计算: __________ (结果写成最简分式)
【答案】
【分析】
首先计算积的乘方,再用同底数幂的除法,最后再化成最简分式即可.
【详解】
解:原式= = x-1y= .
故答案是.
【点睛】
本题主要考查了分式与负指数幂的公式,关键是熟练掌握负指数幂公式,根据负指数幂的公式变形即可得出结果.
10.把化成幂的形式__________.
【答案】
【分析】
根据分数指数幂的定义求解可得.
【详解】
解:因为,
故答案为:
【点睛】
本题主要考查分数指数幂,解题的关键是掌握分数指数幂的定义.
11.利用幂的性质计算:.
【答案】9
【分析】
根据n次方根与分数指数幂的关系即可完成.
【详解】
故答案为:9
【点睛】
本题考查了n次方根与分数指数幂的关系:即(其中n为正整数且a为正实数),幂的运算性质等知识,掌握这两部分知识是关键.
12.用幂的运算性质计算:(结果表示为含幂的形式).
【答案】
【分析】
根据幂的运算性质以及同底数幂的乘除运算
【详解】
解:原式
.
【点睛】
此题主要考查了分数指数幂的性质以及同底数幂的乘除运算,正确化简各数是解题关键.
13.
【答案】
【分析】
首先将括号内化简,化简符号,再根据幂的乘方运算化简即可
【详解】
解:
.
【点睛】
本题考查了分数指数幂,幂的乘法的运算,掌握幂的乘法运算是解题的关键.
14.利用幂的运算性质计算:.
【答案】.
【分析】
先转换成底数相同的幂,再利用同底数幂相乘,底数不变,指数相加即可得出结果.
【详解】
解:
.
【点睛】
本题主要考查幂的运算,正确掌握同底数幂相乘,底数不变,指数相加是解题的关键.
15.计算:+﹣()﹣2+|3﹣|.
【答案】0.
【分析】
利用分数的指数幂的意义,分母有理化,负指数幂的意义,绝对值的性质计算后合并即可.
【详解】
原式=+ ﹣4+3﹣
=3+﹣4+3﹣
=0.
【点睛】
本题考查了分数指数幂的运算,负指数幂的运算,绝对值的意义以及分母有理化运算,熟练掌握实数的运算法则是解题的关键.
16.用幂的运算性质计算:.(结果表示为含幂的形式)
【答案】
【分析】
先将、、转化为底数为2和3的形式,然后按照同底幂的乘法、除法法则运算可得.
【详解】
解:原式
【点睛】
本题考查负分数指数的运算,解题关键是将底数不同的指数转化为底数相同的形式.
1.下列运算中,正确的是( )
A. B.
C. D.
【答案】D
【分析】
根据二次根式的加减法、除法即可得.
【详解】
A、,此项错误
B、若,则,若,则,此项错误
C、与不是同类二次根式,不可合并,此项错误
D、,此项正确
故选:D.
【点睛】
本题考查了二次根式的加减法、除法,熟记运算法则是解题关键.
2.若,则( )
A. B. C. D.
【答案】B
【分析】
先根据零指数幂和整数指数幂对进行化简,再进行大小比较.
【详解】
因为,所以,故答案为B.
【点睛】
本题考查有理数的大小比较、零指数幂和整数指数幂的计算,解题的关键是掌握有理数的大小比较、零指数幂和整数指数幂的计算.
3.当时,下列关于幂的运算正确的是( ).
A. B. C. D.
【答案】A
【详解】
试题分析:选项B应为:;选项C应为:;选项D应为:.
考点:幂的基本运算.
4.把表示成幂的形式是______.
【答案】
【分析】
根据分数指数幂公式即可求出答案.
【详解】
解:.
故答案为:.
【点睛】
本题考查了分数指数幂,熟记分数指数幂运算法则是解题的关键.
5.已知实数满足,那么______.
【答案】
【分析】
根据分数指数的幂运算即可得.
【详解】
则
故答案为:.
【点睛】
本题考查了分数指数的幂运算,熟记运算法则是解题关键.
6.用幂的形式表示:_________.
【答案】
【分析】
根据分数指数幂的法则写出答案即可.
【详解】
解:原式=,
故答案为:.
【点睛】
本题考查了分数指数幂,解题的关键是掌握.
7.把表示成幂的形式是______.
【答案】
【分析】
根据分数指数幂及负指数幂运算法则进行计算即可得出答案.
【详解】
解:原式.
故答案为:.
【点睛】
本题主要考查了分数指数幂,熟练掌握分数指数幂的法则进行计算是解决本题的关键.
8.把化为幂的形式是_______.
【答案】
【分析】
利用立方根的意义以及分数指数幂的意义化简.
【详解】
故答案为:
【点睛】
注意公式 、的应用.
9.已知,则__.
【答案】
【分析】
根据,转化为底数为3的分数指数幂,求得的值.
【详解】
解:,
,
解得,,
故答案为:.
【点睛】
本题考查分数指数幂,解答本题的关键是明确分数指数幂的含义.
10.把方根化为幂的形式:=__________________.
【答案】
【分析】
根据分数指数幂的形式即可得.
【详解】
解:,
故答案为:.
【点睛】
本题考查了分数指数幂,熟练掌握分数指数幂的写法是解题关键.
11.利用幂的性质进行计算:.(结果用幂的形式表示)
【答案】4
【分析】
先把开方运算表示成分数指数幂的形式,再根据同底数乘法、除法法则计算即可.
【详解】
原式
=4
【点睛】
本题考查了分数指数幂.解题的关键是知道开方和分数指数幂之间的关系.
12.计算(结果表示为含幂的形式):.
【答案】.
【分析】
先计算积的乘方的逆用,再计算同底数幂的乘法即可得.
【详解】
解:原式
.
【点睛】
本题考查了积的乘方的逆用、同底数幂的乘法、负整数指数幂,熟练掌握各运算法则是解题关键.
13.利用幂的运算性质进行计算:.
【答案】
【分析】
直接利用分指数幂的性质分别计算得出答案.
【详解】
【点睛】
此题考查实数的运算,正确掌握分数指数幂的性质是解题关键.
14.利用幂的运算性质计算:.
【答案】4
【分析】
直接利用分数指数幂的性质分别化简得出答案.
【详解】
=
=
=
=
=4
【点睛】
此题主要考查了实数运算,正确化简各数是解题关键.
15.计算:.(结果用幂的形式表示)
【答案】3
【分析】
依据分数指数幂的意义即可求出答案..
【详解】
原式.
【点睛】
此题考察分数指数幂的意义,熟记意义即可正确解答.
16.计算:
【答案】答案见解析
【分析】
根据实数计算法则计算即可
【详解】
【点睛】
本题的关键是掌握实数运算法则
相关试卷
这是一份第1讲-实数的概念与开平方(原卷版)-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第1讲-实数的概念与开平方解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第1讲-实数的概念与开平方原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份第3讲-实数的运算-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第3讲-实数的运算解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第3讲-实数的运算原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
这是一份第5讲-实数 单元综合测试-【同步优课】2021-2022学年七年级数学下学期重难点精品讲义(沪教版),文件包含第5讲-实数单元综合测试解析版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx、第5讲-实数单元综合测试原卷版-同步优课2022-2023学年七年级数学下学期重难点精品讲义沪教版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。












