初中数学人教版八年级上册第十一章 三角形综合与测试习题

这是一份初中数学人教版八年级上册第十一章 三角形综合与测试习题，共15页。试卷主要包含了下列图形中，具有稳定性的是，一个多边形的内角和不可能是，下列说法正确的是，若一个三角形三个内角的比是2等内容，欢迎下载使用。
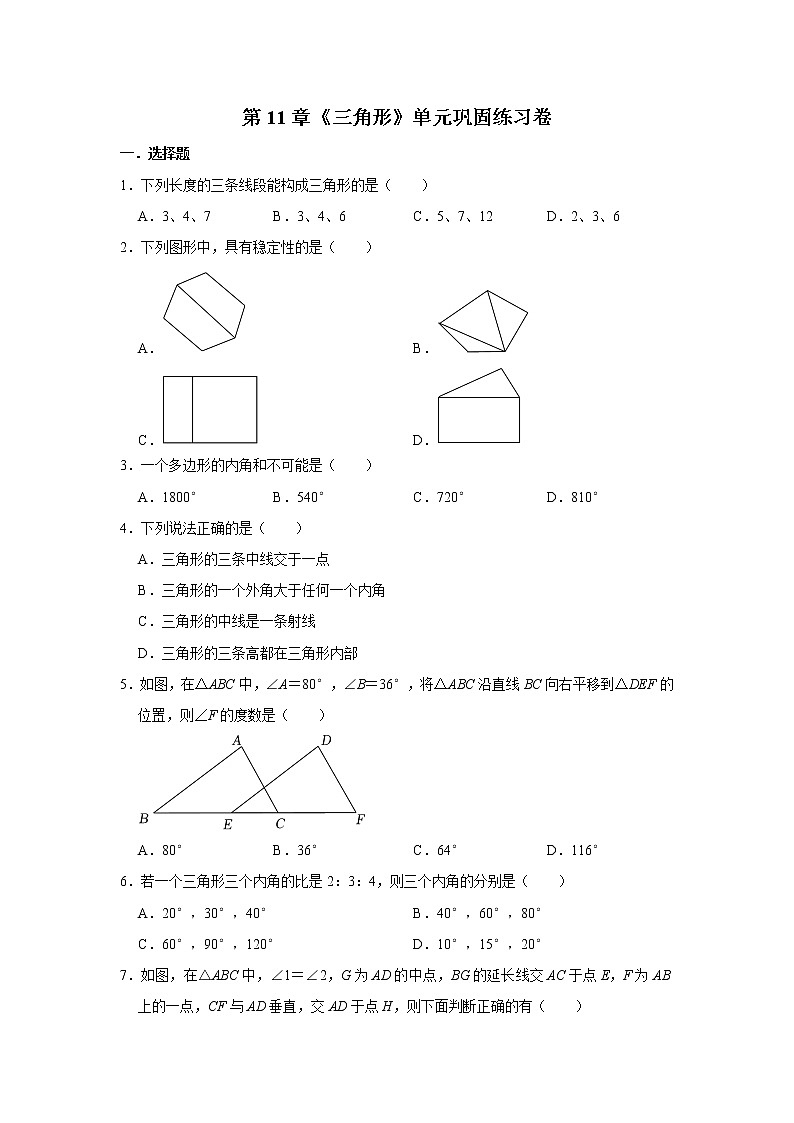
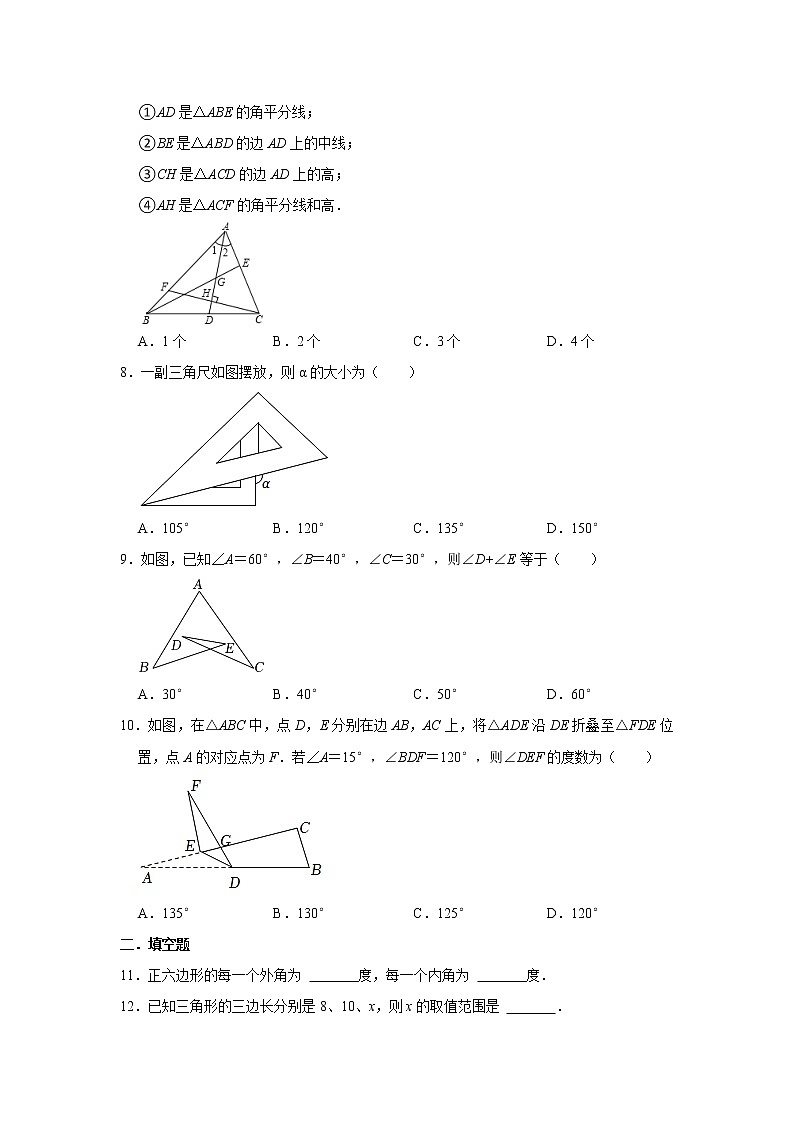
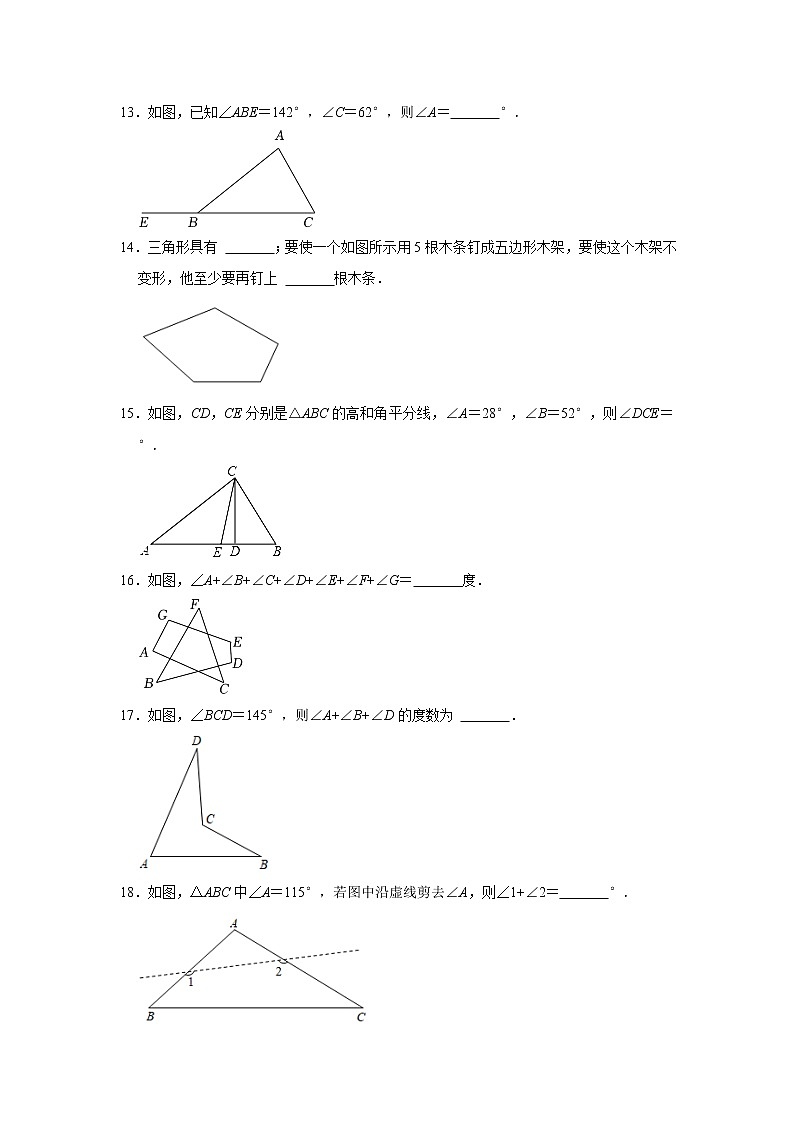
第11章《三角形》单元巩固练习卷一．选择题1．下列长度的三条线段能构成三角形的是（　　）A．3、4、7 B．3、4、6 C．5、7、12 D．2、3、62．下列图形中，具有稳定性的是（　　）A． B． C． D．3．一个多边形的内角和不可能是（　　）A．1800° B．540° C．720° D．810°4．下列说法正确的是（　　）A．三角形的三条中线交于一点 B．三角形的一个外角大于任何一个内角 C．三角形的中线是一条射线 D．三角形的三条高都在三角形内部5．如图，在△ABC中，∠A＝80°，∠B＝36°，将△ABC沿直线BC向右平移到△DEF的位置，则∠F的度数是（　　）A．80° B．36° C．64° D．116°6．若一个三角形三个内角的比是2：3：4，则三个内角的分别是（　　）A．20°，30°，40° B．40°，60°，80° C．60°，90°，120° D．10°，15°，20°7．如图，在△ABC中，∠1＝∠2，G为AD的中点，BG的延长线交AC于点E，F为AB上的一点，CF与AD垂直，交AD于点H，则下面判断正确的有（　　）①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH是△ACD的边AD上的高；④AH是△ACF的角平分线和高．A．1个 B．2个 C．3个 D．4个8．一副三角尺如图摆放，则α的大小为（　　）A．105° B．120° C．135° D．150°9．如图，已知∠A＝60°，∠B＝40°，∠C＝30°，则∠D+∠E等于（　　）A．30° B．40° C．50° D．60°10．如图，在△ABC中，点D，E分别在边AB，AC上，将△ADE沿DE折叠至△FDE位置，点A的对应点为F．若∠A＝15°，∠BDF＝120°，则∠DEF的度数为（　　）A．135° B．130° C．125° D．120°二．填空题11．正六边形的每一个外角为 　   　度，每一个内角为 　   　度．12．已知三角形的三边长分别是8、10、x，则x的取值范围是 　   　．13．如图，已知∠ABE＝142°，∠C＝62°，则∠A＝　   　°．14．三角形具有 　   　；要使一个如图所示用5根木条钉成五边形木架，要使这个木架不变形，他至少要再钉上 　   　根木条．15．如图，CD，CE分别是△ABC的高和角平分线，∠A＝28°，∠B＝52°，则∠DCE＝　   　°．16．如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝　   　度．17．如图，∠BCD＝145°，则∠A+∠B+∠D的度数为 　   　．18．如图，△ABC中∠A＝115°，若图中沿虚线剪去∠A，则∠1+∠2＝　   　°．三．解答题19．已知四边形ABCD的四个外角度数之比为8：6：3：7，求这个四边形各内角度数分别是多少．    20．在如图所示的星形中，∠B＝14°，∠C＝15°，∠F＝16°，∠A+∠D+∠E+∠G＝k•45，求k的值．  21．如图，在△ABC中，AD平分∠BAC交BC于点D，BE平分∠ABC交AD于点E．（1）若∠C＝50°，∠BAC＝60°，求∠ADB的度数；（2）若∠BED＝45°，求∠C的度数．  22．如图，已知△ABC，延长BC至点D，连接AD，E是AD上一点．已知∠B＝45°，∠CAE＝∠D，∠DCE＝∠BAC．（1）求∠ACE的度数：（2）若∠BAC＝25°，求∠CED的度数．     23．（1）如图（1）所示，△ABC中，∠ABC，∠ACB的平分线交于点O，求证：∠BOC＝90°+∠A；（2）如图（2）所示，∠ABC，∠ACD的平分线交于点O，求证：∠BOC＝A；（3）如图（3）所示，∠CBD，∠BCE的平分线交于点O，请直接写出∠BOC与∠A的关系．     24．（1）如图1，在△ABC中，∠B、∠C的平分线BE，CD相交于点F，∠ABC＝40°，∠A＝60°，求∠BFC的度数；（2）如图2，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC＝42°，①求∠CAB的度数；②求∠CAP的度数．         参考答案一．选择题1．【解答】解：A、3+4＝7，不能组成三角形，不符合题意；B、3+4＞6，能够组成三角形，符合题意；C、5+7＝12，不能够组成三角形，不符合题意；D、2+3＜6，不能够组成三角形，不符合题意．故选：B．2．【解答】解：A、图中没有三角形，不具有稳定性，故此选项不符合题意；B、图中均是三角形，具有稳定性，故此选项符合题意；C、图中含有四边形，不具有稳定性，故此选项不符合题意；D、图中含有四边形，不具有稳定性，故此选项不符合题意．故选：B．3．【解答】解：810°不能被180°整除，一个多边形的内角和不可能是810°．故选：D．4．【解答】解：A．三角形的三条中线交于一点，正确；B．三角形的一个外角大于任何和它不相邻的一个内角，错误；C．三角形的中线是一条线段，错误；D．锐角三角形的三条高都在三角形内部，错误；故选：A．5．【解答】解：∵∠A＝80°，∠B＝36°，∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣80°﹣36°＝64°，∵将△ABC沿直线BC向右平移到△DEF的位置，∴∠F＝∠ACB＝64°，故选：C．6．【解答】解：2+3+4＝9，180°×＝40°，180，180，所以三个内角的分别是40°，60°，80°．故选：B．7．【解答】解：对于①，由∠1＝∠2可知AD平分∠BAE，但AD不是△ABE内的线段，由三角形角平分线的概念，故①错误；对于②，BE经过△ABD的边AD的中点G，但BE不是△ABD内的线段，由三角形中线的概念，故②错误；对于③，由于CH⊥AD于H，由三角形高线的概念可知CH是△ACD的边AD上的高，故③正确；对于④，由AH平分∠FAC并且在△ACF内，故AH是△ACF的角平分线．又因为AH⊥CF，所以AH也是△ACF的高，故④正确．故选：B．8．【解答】解：如图，由题意得：∠ABC＝45°，∠1＝30°，∠C＝90°，∴∠2＝∠ABC﹣∠1＝15°，∴∠α＝∠2+∠C＝105°．故选：A．9．【解答】解：连接BC，如右图所示，∵∠A＝60°，∠ABE＝40°，∠ACD＝30°，∴∠1+∠2＝180°﹣∠A﹣∠ABE﹣∠ACD＝180°﹣60°﹣40°﹣30°＝50°，∵∠D+∠E＝∠1+∠2，∴∠D+∠E＝50°，故选：C．10．【解答】解：由题意得，∠ADE＝∠FDE，∠AED＝∠FED，∵∠BDF＝120°，∴∠ADF＝180°﹣120°＝60°，∴，∴∠DEA＝180°﹣∠A﹣∠ADE＝180°﹣15°﹣30°＝135°，∵△ADE沿DE折叠至△FDE位置，∴∠DEF＝∠DEA＝135°，故选：A．二．填空题11．【解答】解：因为正六边形的外角和是360°，所以正六边形的每一个外角为360°÷6＝60°；因为多边形的内角和公式为（n﹣2）•180°，所以正六边形的内角和为（6﹣2）×180°＝720°，每一个内角是＝120°．故答案为：60，120．12．【解答】解：根据三角形的三边关系可得：10﹣8＜x＜10+8，即2＜x＜18，故答案为：2＜x＜18．13．【解答】解：∵∠ABE＝142°，∠ABE是△ABC的外角，∠C＝62°，∴∠ABE＝∠A+∠C，∴∠A＝∠ABE﹣∠C＝＝80°，故答案为：80．14．【解答】解：∵三角形具有稳定性，∴要使这个木架不变形，至少要再钉上如图中虚线所示的2根木条，故答案为：稳定性；2．15．【解答】解：∵∠A＝28°，∠B＝52°，∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣28°﹣52°＝100°，∵CE是△ABC的角平分线，∴∠ACE＝∠ACB＝50°，∴∠CED＝∠A+∠ACE＝28°+50°＝78°，∵CD是高，∴∠CDE＝90°，∴∠DCE＝90°−∠CED＝90°−78°＝12°，故答案为：12．16．【解答】解：如图：∵∠1＝∠B+∠2，∠2＝∠F+∠C，∴∠1＝∠B+∠F+∠C，∴∠A+∠1+∠D+∠E+∠G＝∠A+∠B+∠C+∠F+∠D+∠E+∠G＝（5﹣2）×180°＝540°．故答案为：540．17．【解答】解：延长DC交AB于E，∠CEB是△ADE的一个外角，∴∠CEB＝∠A+∠D，同理，∠BCD＝∠CEB+∠B，∴∠A+∠B+∠D＝∠CEB+∠B＝∠BCD＝145°，故答案为：145°．18．【解答】解：∵∠A＝115°，∴∠B+∠C＝65°，∵∠1+∠2+∠B+∠C＝360°，∴∠1+∠2＝360°﹣65°＝295°．故答案为：295．三．解答题19．【解答】解：设四边形的四个外角的度数分别为8k，6k，3k，7k，则由8k+6k+3k+7k＝360，得到k＝15°．从而四个外角分别为120°，90°，45°，105°．所以这个四边形各内角的度数分别为60°，90°，135°和75°．20．【解答】解：如图：设AE与CG相交于M，AE与BF相交于N，BF与CG相交于H，BF与DG相交于K，AE与DG相交于J，由三角形的外角性质得，∠A+∠D＝∠AJG，∠B+∠E＝∠ENF，∠C+∠F＝∠GHK，∴∠HKG＝∠AJG+∠ENF＝∠A+∠D+∠B+∠E，∵∠HKG+∠GHK+∠G＝180°，∴∠A+∠D+∠B+∠E+∠C+∠F+∠G＝180°，即∠A+∠B+∠C+∠D+∠E+∠F+∠G＝180°．∵∠B＝14°，∠C＝15°，∠F＝16°，∠A+∠D+∠E+∠G＝k•45，∴∠A+∠D+∠E+∠G＝180°﹣14°﹣15°﹣16°＝135°＝3°×45，∴k的值为3°．21．【解答】解：（1）∵AD平分∠BAC，∠BAC＝60°，∴．∵∠ADB是△ADC的外角，∠C＝50°，∴∠ADB＝∠C+∠DAC＝80°；（2）∵AD平分∠BAC，BE平分∠ABC，∴∠BAC＝2∠BAD，∠ABC＝2∠ABE．∵∠BED是△ABE的外角，∠BED＝45°，∴∠BAD+∠ABE＝∠BED＝45°．∴∠BAC+∠ABC＝2（∠BAD+∠ABE）＝90°．∵∠BAC+∠ABC+∠C＝180°，∴∠C＝180°﹣（∠BAC+∠ABC）＝90°．22．【解答】解：（1）∵∠ACD＝∠B+∠BAC，即∠ACE+∠DCE＝∠B+∠BAC，而∠B＝45°，∠DCE＝∠BAC．∴∠ACE＝∠B＝45°；（2）∵∠DCE＝∠BAC＝25°，∠ACE＝45°，∴∠ACD＝25°+45°＝70°，∵∠D+∠CAE+∠ACD＝180°，∴∠CAE+∠ACD＝180°﹣70°＝110°，∵∠CAE＝∠D，∴∠D＝×110°＝55°，∴∠CED＝180°﹣25°﹣55°＝100°．23．【解答】证明：（1）∵在△ABC中，OB、OC分别是∠ABC、∠ACB的平分线，∴∠1＝∠ABC，∠2＝∠ACB，∴∠1+∠2＝（∠ABC+∠ACB）＝（180°﹣∠A）＝×（180°﹣x°）＝90°﹣∠A，∴∠BOC＝180°﹣（∠1+∠2）＝180°﹣（90°﹣∠A）＝90°+∠A；（2）∵∠OCD是△BCO的外角，∴∠O＝∠2﹣∠1，又∵BO平分∠ABC，CO平分∠ACD，∴∠1＝∠ABC，∠2＝∠ACD，∴∠O＝（∠ACD﹣∠ABC），∵∠A＝∠ACD﹣∠ABC，∴∠O＝∠BAC；（3）∵BO、CO为△ABC中∠ABC、∠ACB外角的平分线，∴∠2＝∠BCE，∠1＝∠DBC，∵∠BCE＝∠A+∠ABC，∠DBC＝∠A+∠ACB，∴∠2＝（∠A+∠ABC）、∠1＝（∠A+∠ACB），由三角形内角和定理得，∠BDC＝180°﹣∠1﹣∠2＝180°﹣[∠A+（∠A+∠ABC+∠ACB）]＝180°﹣（∠A+180°）＝90°﹣∠A．24．【解答】解：（1）∵∠ABC＝40°，∠A＝60°，∴∠ACB＝80°，∵∠ABC、∠ACB的平分线相交于点F，∴∠FBC＝∠ABC＝20°，∠FCB＝∠ACB＝40°，∴∠BFC＝180°﹣（∠FBC+∠FCB）＝120°；（2）①在△ABC中，∠ACD＝∠BAC+∠ABC，在△PBC中，∠PCD＝∠BPC+∠PBC，∵PB、PC分别是∠ABC和∠ACD的平分线，∴∠PCD＝∠ACD，∠PBC＝∠ABC，∴∠PCD＝∠BPC+∠PBC＝42°+∠ABC，∴∠ACD＝∠ABC+42°，∴∠ACD﹣∠ABC＝84°，∴∠BAC＝∠ACD﹣∠ABC＝84°，即∠CAB＝84°．②作PE⊥BA于E，PF⊥AC于F，PG⊥BC于G，∴PE＝PG，PF＝PG，∴PE＝PF，∴AP平分∠CAE，∴∠CAP＝∠CAE＝×（180°﹣84°）＝48°．