沪科版九年级上册21.2 二次函数的图象和性质备课课件ppt

这是一份沪科版九年级上册21.2 二次函数的图象和性质备课课件ppt，共16页。PPT课件主要包含了描点连线，Y轴左侧，Y轴右侧，增大而增大，增大而减小等内容，欢迎下载使用。

重点在于领悟二次函数渗透的数学思想：数形结合
结合图象讨论性质是数形结合的研究函数的重要方法．我们得从最简单的二次函数开始逐步深入地讨论一般二次函数的图象和性质．
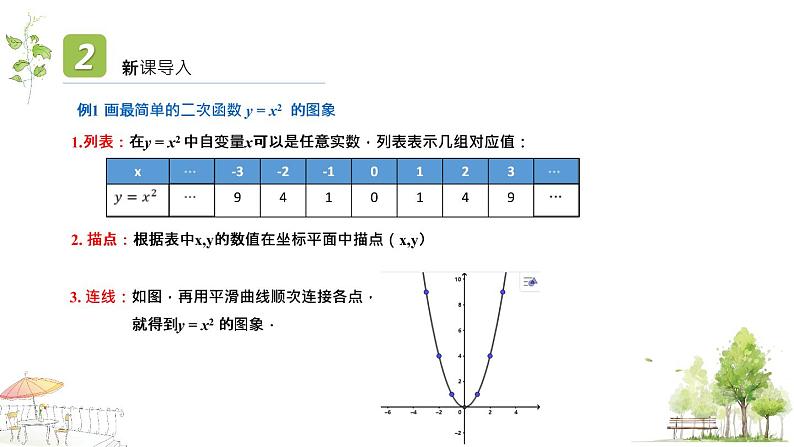
例1 画最简单的二次函数 y = x2 的图象
1.列表：在y = x2 中自变量x可以是任意实数，列表表示几组对应值：
2. 描点：根据表中x,y的数值在坐标平面中描点（x,y）
3. 连线：如图，再用平滑曲线顺次连接各点， 就得到y = x2 的图象．
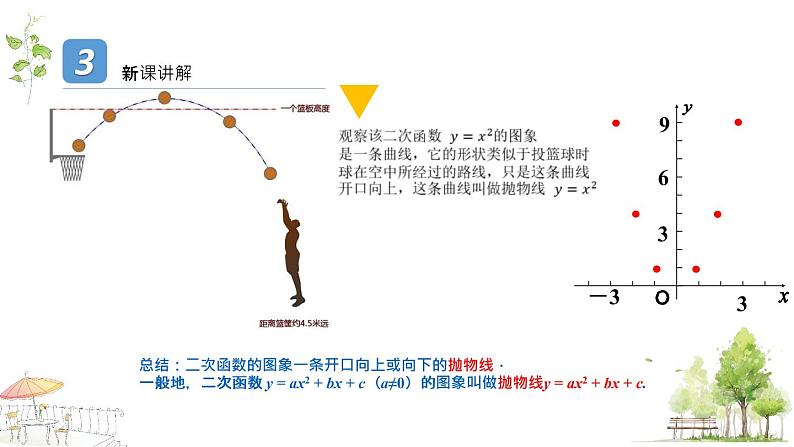
总结：二次函数的图象一条开口向上或向下的抛物线． 一般地，二次函数 y = ax2 + bx + c（a≠0）的图象叫做抛物线y = ax2 + bx + c.
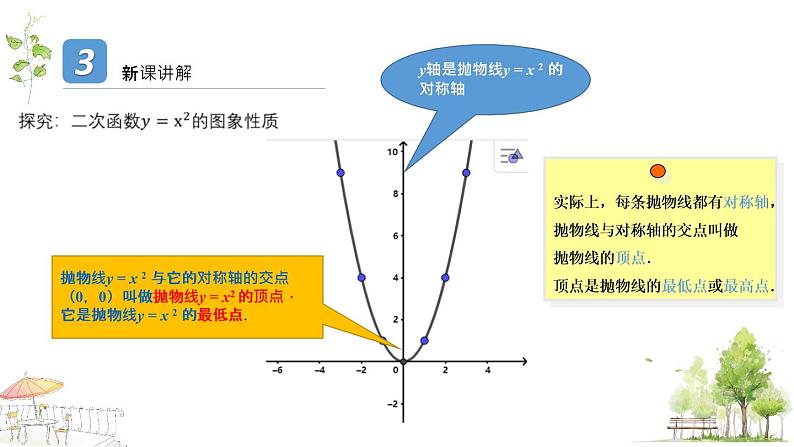
y轴是抛物线y = x 2 的对称轴
抛物线y = x 2 与它的对称轴的交点（0，0）叫做抛物线y = x2 的顶点，它是抛物线y = x 2 的最低点．
实际上，每条抛物线都有对称轴，抛物线与对称轴的交点叫做抛物线的顶点．顶点是抛物线的最低点或最高点．
开口都向上，顶点是原点而且是抛物线的最低点，对称轴是 y 轴.
a 的值越大，抛物线的开口程度越小．
二次函数y=ax2的性质
|a|越大，抛物线开口程度越小，反之亦然
例1 抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大；在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
法1：可以利用y=ax2 的性质直接解题，重点在于对函数模型的熟练掌握。
法2：二次函数在于考察数形结合的思想，同学们可以通过绘制图形来归纳总结
利用对称性解题，地球人都知道！！
1、课本P10页练习2、同步学案21·2第1课时3、预习第2课时
①当抛物线过点B时，抛物线开口程度最小，a取最大值；②当抛物线过点D时，抛物线开口程度最大，a取最小值；