第07讲 抛物线中等腰三角形的存在性问题专题探究-【专题突破】2022-2023学年九年级数学上学期重难点及章节分类精品讲义(浙教版)

这是一份第07讲 抛物线中等腰三角形的存在性问题专题探究-【专题突破】2022-2023学年九年级数学上学期重难点及章节分类精品讲义(浙教版)，文件包含第07讲抛物线中等腰三角形的存在性问题专题探究-专题突破2022-2023学年九年级数学上学期重难点及章节分类精品讲义浙教版解析版docx、第07讲抛物线中等腰三角形的存在性问题专题探究-专题突破2022-2023学年九年级数学上学期重难点及章节分类精品讲义浙教版原卷版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
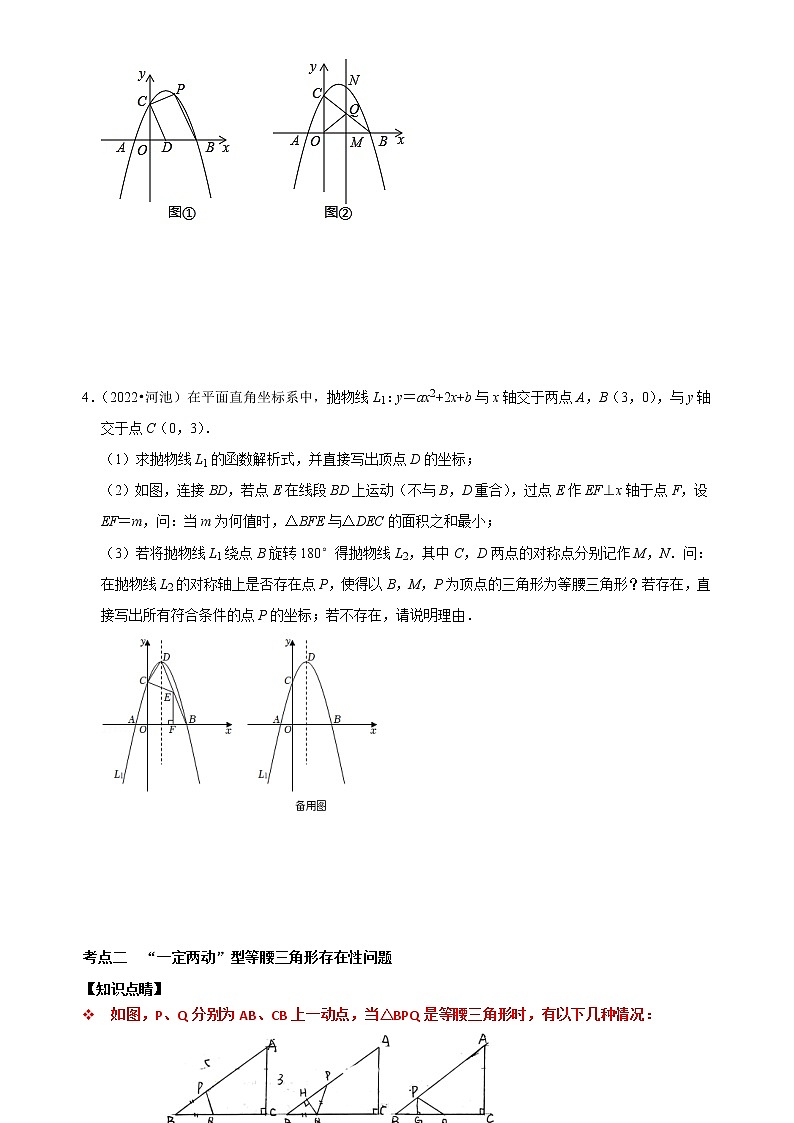
第7讲  抛物线中等腰三角形的存在性问题专题探究考点一  “两定一动”型等腰三角形存在性问题【知识点睛】        如图，已知定点A、O，在x轴上找点P，使△OAP为等腰三角形则P1、P2、P3、P4即为符合题意的点P解决策略：（有时也可用两点间距离公式求值）即：①当OA=OP时，以O点为圆心，OA长为半径画圆，与目标直线x轴的交点即为所求点②当OA=AP时，以A点为圆心，OA长为半径画圆，与目标直线x轴的交点即为所求点    ③当AP=OP时，线段OA的中垂线与目标直线x轴的交点即为所求点【类题训练】1．（2019秋•云梦县期末）如图，已知抛物线y＝x2+bx+4与x轴相交于A、B两点，与y轴相交于点C，若已知A点的坐标为A（﹣2，0）．（1）求抛物线的解析式；（2）求线段BC所在直线的解析式；（3）在抛物线的对称轴上是否存在点P，使△ACP为等腰三角形？若存在，求出符合条件的P点坐标；若不存在，请说明理由．       2．（2021秋•南昌期末）如图，二次函数y＝ax2+bx+c的图象交x轴于A（﹣2，0），B（1，0），交y轴于C（0，2）．（1）求二次函数的解析式；（2）连接AC，在直线AC上方的抛物线上是否存在点N，使△NAC的面积最大，若存在，求出这个最大值及此时点N的坐标，若不存在，说明理由；（3）若点M在x轴上，是否存在点M，使以B、C、M为顶点的三角形是等腰三角形，若存在，直接写出点M的坐标；若不存在，说明理由．         3．（2020•佛山模拟）如图①，已知抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C．（1）求抛物线的解析式；（2）点D的坐标为（1，0），点P为第一象限内抛物线上的一点，求四边形BDCP面积的最大值；（3）如图②，动点M从点O出发，以每秒2个单位长度的速度向点B运动，到达点B时停止运动，且不与点O、B重合．设运动时间为t秒，过点M作x轴的垂线交抛物线于点N，交线段BC于点Q，连接OQ，是否存在t值，使得△BOQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．     4．（2022•河池）在平面直角坐标系中，抛物线L1：y＝ax2+2x+b与x轴交于两点A，B（3，0），与y轴交于点C（0，3）．（1）求抛物线L1的函数解析式，并直接写出顶点D的坐标；（2）如图，连接BD，若点E在线段BD上运动（不与B，D重合），过点E作EF⊥x轴于点F，设EF＝m，问：当m为何值时，△BFE与△DEC的面积之和最小；（3）若将抛物线L1绕点B旋转180°得抛物线L2，其中C，D两点的对称点分别记作M，N．问：在抛物线L2的对称轴上是否存在点P，使得以B，M，P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．    考点二  “一定两动”型等腰三角形存在性问题【知识点睛】        如图，P、Q分别为AB、CB上一动点，当△BPQ是等腰三角形时，有以下几种情况：   ①BP=BQ          ②BQ=PQ           ③BP=PQ 解决策略：  即BQ=PQ可转化为: ;BP=PQ可转化为:☆特别地：当题目给出的数据还好时，也可选择用代数法来分类讨论等腰三角形步骤如下：①根据点的坐标，表示出三边的平方          ②根据等腰三角形的性质，可得到两两相等的的三个方程          ③分别解出这三个方程，再依据结果判断是否存在【类题训练】1．（2021•陕西模拟）如图，在平面直角坐标系中，一抛物线的对称轴为直线x＝1，且该抛物线与y轴负半轴交于C点，与x轴交于A，B两点，其中B点的坐标为（3，0），且OB＝OC．（1）求此抛物线的函数表达式；（2）若平行于x轴的直线与该抛物线交于M、N两点（其中点M在点N的右侧），在x轴上是否存在点Q，使△MNQ是以MN为一直角边的等腰直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由． 2．（2021秋•铅山县期末）如图1，在平面直角坐标系中，抛物线y＝x2+bx+c经过A（1，0），C（0，5）两点，与x轴的另一交点为B．（1）求抛物线解析式；（2）若点M为直线BC下方抛物线上一动点，MN⊥x轴交BC于点N．①当线段MN的长度最大时，求此时点M的坐标及线段MN的长度；②如图2，连接BM，当△BMN是等腰三角形时，求此时点M的坐标．  3．（2021秋•大连期末）在平面直角坐标系中，抛物线y＝ax2+bx﹣3（a，b是常数，a＞0）与x轴交于A、B两点，与y轴交于点C，对称轴为直线x＝1．（1）填空：b＝　  　（用含a的代数式表示）；（2）当﹣1≤x≤0时，抛物线上的点到x轴的最大距离为5，求a的值；（3）若点A的坐标为（﹣1，0），点E的坐标为（x，0）（其中x≥0），点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，求出点E的坐标；若不存在，请说明理由．          【课后综合练习】1．（2022春•北碚区校级期末）如图，已知点（0，）在抛物线C1：y＝x2+bx+c上，且该抛物线与x轴正半轴有且只有一个交点A，与y轴交于点B，点O为坐标原点．（1）求抛物线C1的解析式；（2）抛物线C1沿射线BA的方向平移个单位得到抛物线C2，如图2，抛物线C2与x轴交于C，D两点，与y轴交于点E，点M在抛物线C2上，且在线段ED的下方，作MN∥y轴交线段DE于点N，连接ON，记△EMD的面积为S1，△EON的面积为S2，求S1+2S2的最大值；（3）如图3，在（2）的条件下，抛物线C2的对称轴与x轴交于点F，连接EF，点P在抛物线C2上且在对称轴的右侧，满足∠PEC＝∠EFO．①直接写出P点坐标；②是否在抛物线C2的对称轴上存在点H，使得△PDH为等腰三角形，若存在，请直接写出H点的坐标；若不存在请说明理由．