初中数学人教版七年级上册第四章 几何图形初步综合与测试学案设计

这是一份初中数学人教版七年级上册第四章 几何图形初步综合与测试学案设计，共11页。
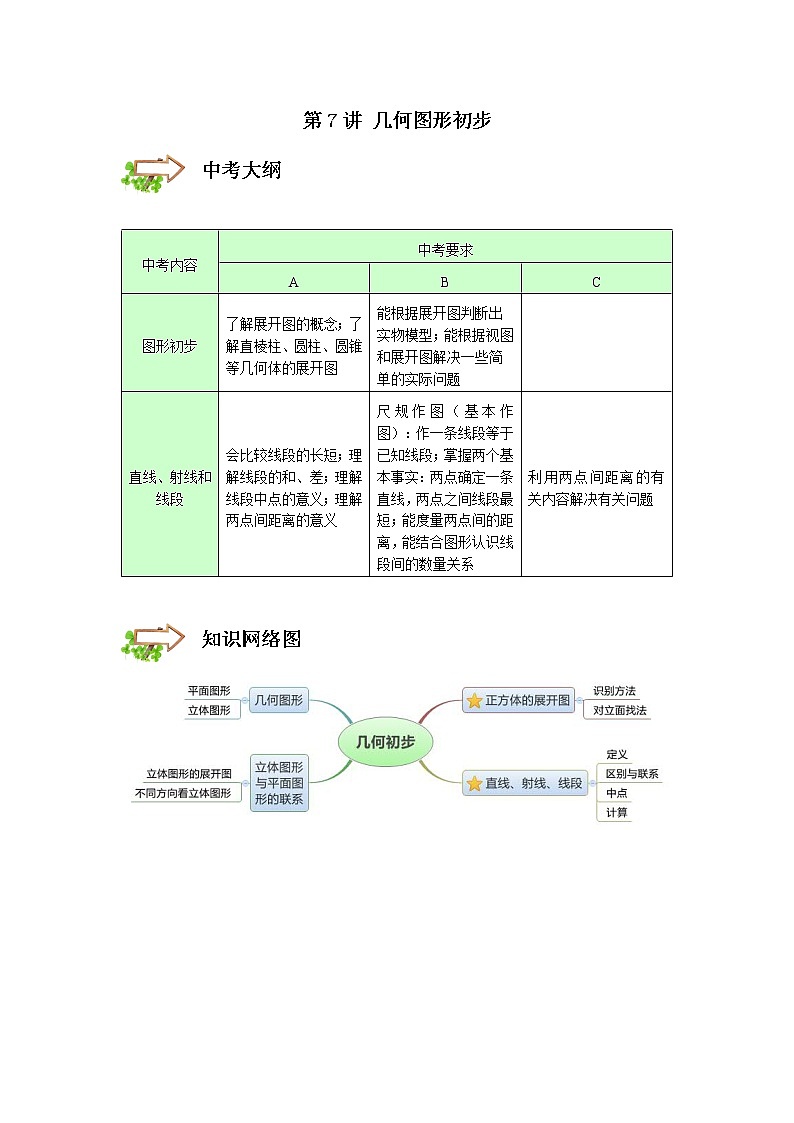
第7讲 几何图形初步 中考内容中考要求ABC图形初步了解展开图的概念；了解直棱柱、圆柱、圆锥等几何体的展开图能根据展开图判断出实物模型；能根据视图和展开图解决一些简单的实际问题 直线、射线和线段会比较线段的长短；理解线段的和、差；理解线段中点的意义；理解两点间距离的意义尺规作图（基本作图）：作一条线段等于已知线段；掌握两个基本事实：两点确定一条直线，两点之间线段最短；能度量两点间的距离，能结合图形认识线段间的数量关系利用两点间距离的有关内容解决有关问题   
1图形的认识一．  图形分类 几何图形：长方体、圆柱、球、长（正）方形、圆、线段、点等，以及小学学习过的三角形、四边形等，都是从形形色色的物体外形中得出的，它们都是几何图形． 立体图形：有些几何图形（如长方体、正方体、圆柱、圆锥、球等）的各部分不都在同一平面内，它们是立体图形．棱柱、棱锥也是常见的立体图形．如下图中的这些生活中常见的物体都是立体图形． 平面图形：有些几何图形（如线段、角、三角形、长方形、圆等）的各部分都在同一平面内，它们都是平面图形．如下面这些图形：二．  立体图形与平面图形的联系： 立体图形中某些部分是平面图形，例如长方体的侧面是长方形； 对于一些立体图形，常把它们转化为平面图形来研究和处理．从不同方向来看立体图形，往往会得到不同形状的平面图形； 有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以张开成平面图形，这样的平面图形称为相应立体图形的展开图． 【例】（2017秋•郑州期末）乐乐玩橡皮泥时，将一个底面直径为4cm，高为4cm的圆柱，捏成底面直径为3.2cm的圆柱，则圆柱的高变成了（　　）A．7.5cm B．6.25cm C．5cm D．4.75cm 　【练习】（2017秋•汝州市校级期中）若一个棱柱有10个顶点，则下列说法正确的是（　　）A．这个棱柱有4个侧面 B．这个棱柱有5条侧棱C．这个棱柱的底面是十边形 D．这个棱柱是一个十棱柱 【例】（2017秋•福田区校级期中）n棱柱的棱数与面数之和等于（　　）A．3n B．4n+2 C．3n+2 D．2n+2 　【例】（2017秋•揭西县校级月考）一个圆柱体削去12立方分米后，正好削成一个与它等底等高的圆锥，这个圆锥体体积是（　　）立方分米．A．24 B．，12 C．6 D．18 　【练习】（2017秋•汝州市校级月考）用一张长20cm，宽8cm的纸片围成一个高为8cm的圆柱，则该圆柱的底面半径是（　　）A．10cm B．cm C．20cm D．cm 2点、线、面、体 体：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体，简称体．正方体长方体三棱柱三棱锥四棱锥 圆柱圆锥球  面：包围着体的是面，面有平面和曲面两种． 线：面与面相交的地方形成线． 点：线与线相交的地方是点． 点、线、面、体的关系：点动成线，线动成面，面动成体． 【例】（2018•河北模拟）将下列各选项中的平面图形绕轴旋转一周，可得到如图所示的立体图形的是（　　）A． B． C． D． 　【练习】（2017秋•文登区期末）将下列图形绕着直线旋转一周正好得到如图所示的图形的是（　　）A． B． C． D． 　【例】（2016秋•江阴市期末）如图，把左边的图形绕着给定的直线旋转一周后形成的几何体是（　　）A． B． C． D． 　　【巩固】（2017秋•烟台期中）将下面平面图形绕直线l旋转一周，可得到如图所示立体图形的是（　　）A． B． C． D．   3直线、射线、线段一．  直线、射线、线段的概念 在直线的基础上定义射线、线段：（1）直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点．（2）直线上两点和中间的部分叫线段，这两个点叫线段的端点． 在线段的基础上定义直线、射线：（1）把线段向一方无限延伸所形成的图形叫射线．（2）把线段向两方无限延伸所形成的图形是直线．二．  直线1．  点的表示方法：我们经常用一个大写的英文字母表示点：，，，， ．2．  关于直线的基本事实：经过两点有一条直线，并且只有一条直线，也称为“两点确定一条直线”．3．  直线的表示方法：（1）用一个小写字母来表示，如下图表示为直线．注意：在直线的表示前面必须加上“直线”二字．（2）用一条直线上的两点来表示这条直线，如下图表示为直线．注意：是两个大写字母，不分先后顺序，因此也可以写作直线．4．  点与直线的关系：（1）一个点在一条直线上，也可以说这条直线经过这个点．（2）一个点在一条直线外，也可以说直线不经过这个点．5．  相交：当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做它们的交点 三．  射线射线的表示方法：（1）用一个小写字母来表示，如下图表示为射线．注意：在射线的表示前面必须加上“射线”二字．（2）用射线的端点和射线上的一点来表示，如下图表示为射线．注意：第一个大写字母表示射线的端点，第二个大写字母表示射线上的点，因此两个字母分先后顺序，不能写作射线．四．  线段1．  线段的表示方法：（1）用一个小写字母来表示：如下图表示为线段．注意：在线段的表示前面必须加上“线段”二字．（2）用线段上的两点来表示这个线段，如下图表示为线段．注意：是两个大写字母，不分先后顺序，因此也可以写作线段．2．  线段长短的比较（1）测量法：用刻度尺分别测量出线段的长度，通过长度来比较线段的长短；（2）作图法：把其中一条线段移到另一条上作比较．尺规作图：用无刻度的直尺和圆规作图，这就是尺规作图．3．  中点：把线段分成两条相等的线段的点叫做这条线段的中点．，  三等分点：把线段分成三条相等的线段的两个点叫做这条线段的三等分点．， 4．  关于线段的基本事实：两点的所有连线中，线段最短，简称“两点之间，线段最短”．5．  两点的距离：连接两点间的线段的长度，叫做这两点的距离．五．  直线、射线、线段的主要区别：类型端点表示方法是否可度量是否可延长直线个直线直线或直线否无射线个射线射线，是端点否有反向延长线线段个线段线段或线段是有延长线及反向延长线 【例】（2017秋•福田区期末）如图，AB=24，点C为AB的中点，点D在线段AC上，且AD：CB=1：3，则DB的长度为（　　）A．12 B．18 C．16 D．20 　【练习】（2017秋•郓城县期末）如图，点C在线段AB上，点D是AC的中点，如果CB=CD，AB=10.5cm，那么BC的长为（　　）A．A2.5cm B．3cm C．4.5cm D．6cm 　【练习】（2017秋•利川市期末）如图，点C为线段AB上一点，点C将AB分成2：3两部分，M是AC的中点，N是BC的中点，若AN=35cm．求AB的长． 　【巩固】（2017秋•涡阳县期末）如图，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点（1）求线段MN的长；（2）若C为线段AB上任意一点，满足AC+CB=acm，其他条件不变，你能猜出线段MN的长度吗？并说明理由． 　【练习】（2017秋•前郭县期末）如图，点A、B、C、D在同一直线上，且AB：BC：CD=2：3：5（1）若AD=24cm，求AB、BC、CD的长；（2）若点M、N是AC、CD中点，且AD=a，求MN的长．   综合应用一．选择题（共5小题）1．已知线段AB＝5cm，线段AC＝4cm，则线段BC的长度为（　　）A．9cm B．1cm C．9cm或1cm D．无法确定2．如图，C是线段AB上的点，D是线段AC的中点，E是线段BC的中点，若DE＝10，则AB的长为（　　）A．10 B．20 C．30 D．403．已知线段AB＝12cm．C是AB的中点．在线段AB上有一点D，且CD＝2cm．则AD的长是（　　）A．8cm B．8cm或2cm C．8cm或4cm D．2cm或4cm4．如图，点C是AB的中点，点D是BC的中点，现给出下列等式：①CD＝AC﹣DB，②CD＝AB，③CD＝AD﹣BC，④BD＝2AD﹣AB．其中正确的等式编号是（　　）A．①②③④ B．①②③ C．②③④ D．②③5．直线a上有5个不同的点A、B、C、D、E，则该直线上共有（　　）条线段．A．8 B．9 C．12 D．10二．解答题（共3小题）6．如图，线段AB＝8，点C是线段AB的中点，点D是线段BC的中点．（1）求线段AD的长；（2）若在线段AB上有一点E，CE＝BC，求AE的长．7．已知线段AB＝16，在直线AB上截取线段BC＝10，点P、Q分別是AB、AC的中点．（1）线段PQ的长度为　   　；（2）若AB＝m，BC＝n，其它条件不变，求线段PQ的长度；（3）分析（1）（2）的结论，你从中发现了什么规律？8．如图，直线1上有A，B两点，AB＝12cm，点O是线段AB上的一点，OA＝2OB．（1）OA＝　   　cm，OB＝　   　cm；（2）若点C是线段AB上一点（点C不与点AB重合），且满足AC＝CO+CB，求CO的长；（3）若动点P，Q分别从A，B同时出发，向右运动，点P的速度为2cm/s，点Q的速度为1cm/s．设运动时间为t（s），当点P与点Q重合时，P，Q两点停止运动．求当t为何值时，2OP﹣OQ＝4（cm）；