专题04 三角形单元综合提优专练- 2022-2023学年八年级上册数学专题训练（人教版）

这是一份专题04 三角形单元综合提优专练- 2022-2023学年八年级上册数学专题训练（人教版），文件包含专题04三角形单元综合提优专练解析版-2022-2023学年八年级上册数学专题训练人教版docx、专题04三角形单元综合提优专练原卷版-2022-2023学年八年级上册数学专题训练人教版docx等2份试卷配套教学资源，其中试卷共50页， 欢迎下载使用。
专题04三角形单元综合提优专练（解析版）
学校:___________姓名：___________班级：___________考号：___________


一、单选题
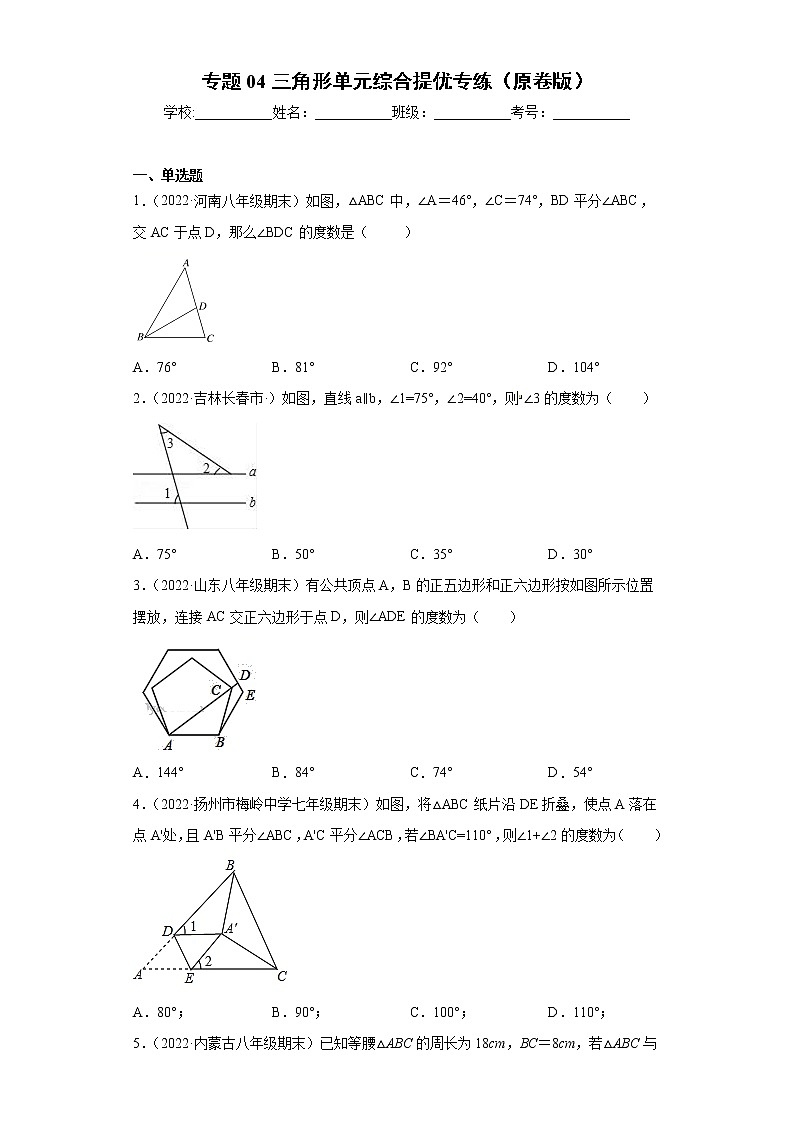
1．（2022·河南八年级期末）如图，△ABC中，∠A＝46°，∠C＝74°，BD平分∠ABC，交AC于点D，那么∠BDC的度数是（ ）

A．76° B．81° C．92° D．104°
【答案】A
【分析】
根据三角形的内角和为180°，可得∠A+∠C+∠ABC=180°，然后根据△ABC中，∠A＝46°，∠C＝74°，求得∠ABC=60°，然后根据角平分线的性质，可得∠ABD=30°，再根据三角形的外角性质，可得∠BDC=∠A+∠ABD=76°.
【详解】
∵△ABC中，∠A=46°，∠C=74°，
∴∠ABC=60°，
∵BD为∠ABC平分线，
∴∠ABD=∠CBD=30°，
∵∠BDC为△ABD外角，
∴∠BDC=∠A+∠ABD=76°，
故选A
【点睛】
此题主要考查了三角形的内角和外角的性质，解题关键是构造合适的角的和差关系，然后根据角平分线的性质求解即可.
2．（2022·吉林长春市·）如图，直线a∥b，∠1=75°，∠2=40°，则∠3的度数为（　　）

A．75° B．50° C．35° D．30°
【答案】C
【详解】
【分析】根据两直线平行，内错角相等可以得出∠4=∠1=75°，再根据三角形外角的性质即可得出答案.
【详解】∵a∥b，
∴∠4=∠1=75°，
∴∠2+∠3=∠4=75°，
∵∠2=40°，
∴∠3=75°﹣40°=35°，
故选C．

【点睛】本题考查了平行线的性质以及三角形外角的性质，结合图形熟练应用相关性质解题是关键.
3．（2022·山东八年级期末）有公共顶点A，B的正五边形和正六边形按如图所示位置摆放，连接AC交正六边形于点D，则∠ADE的度数为（　　）

A．144° B．84° C．74° D．54°
【答案】B
【详解】
正五边形的内角是∠ABC==108°，∵AB=BC，∴∠CAB=36°，正六边形的内角是∠ABE=∠E==120°，∵∠ADE+∠E+∠ABE+∠CAB=360°，∴∠ADE=360°–120°–120°–36°=84°，故选B．
4．（2022·扬州市梅岭中学七年级期末）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C=110°，则∠1+∠2的度数为（　　）

A．80°； B．90°； C．100°； D．110°；
【答案】A
【详解】
分析：连接AA′．首先求出∠BAC，再证明∠1+∠2=2∠BAC即可解决问题．
详解：连接AA′．

∵A'B平分∠ABC，A'C平分∠ACB，∠BA'C=110°，∴∠A′BC+∠A′CB=70°，∴∠ABC+∠ACB=140°，∴∠BAC=180°﹣140°=40°．
∵∠1=∠DAA′+∠DA′A，∠2=∠EAA′+∠EA′A．
∵∠DAA′=∠DA′A，∠EAA′=∠EA′A，∴∠1+∠2=2（∠DAA′+∠EAA′）=2∠BAC=80°．
故选A．
点睛：本题考查了三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识，属于中考常考题型．
5．（2022·内蒙古八年级期末）已知等腰△ABC的周长为18cm，BC＝8cm，若△ABC与△A′B′C′全等，则△A′B′C′的腰长等于（　　）
A．8cm B．2cm或8cm C．5cm D．8cm或5cm
【答案】D
【详解】
分析：因为BC是腰是底不确定，因而有两种可能，当BC是底时，△ABC的腰长是5cm，当BC是腰时，腰长就是8cm，且均能构成三角形，因为△A′B′C′与△ABC全等，所以△A′B′C′的腰长也有两种相同的情况：8cm或5cm．
详解：分为两种情况：当BC是底时，△ABC的腰长是5cm，
∵△ABC与△A′B′C′全等，
∴△A′B′C′的腰长也是5cm；
当BC是腰时，腰长就是8cm，且均能构成三角形，
∵△A′B′C′与△ABC全等，
∴△A′B′C′的腰长也等于8cm，
即△A′B′C′的腰长为8cm或5cm，
故选D．
点睛：本题考查了全等三角形的性质和等腰三角形的性质的应用，用了分类讨论思想．
6．（2022·内蒙古中考真题）如图，AB∥CD，点E在线段BC上，CD=CE,若∠ABC=30°，则∠D为（　　）

A．85° B．75° C．60° D．30°
【答案】B
【详解】
分析：先由AB∥CD，得∠C=∠ABC=30°，CD=CE，得∠D=∠CED，再根据三角形内角和定理得，∠C+∠D+∠CED=180°，即30°+2∠D=180°，从而求出∠D．
详解：∵AB∥CD，
∴∠C=∠ABC=30°，
又∵CD=CE，
∴∠D=∠CED，
∵∠C+∠D+∠CED=180°，即30°+2∠D=180°，
∴∠D=75°．
故选B．
点睛：此题考查的是平行线的性质及三角形内角和定理，解题的关键是先根据平行线的性质求出∠C，再由CD=CE得出∠D=∠CED，由三角形内角和定理求出∠D．
7．（2022·广东九年级一模）如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E,若∠A=54°，∠B=48°，则∠CDE的大小为（　　）

A．44° B．40° C．39° D．38°
【答案】C
【详解】
【分析】根据三角形内角和得出∠ACB，利用角平分线得出∠DCB，再利用平行线的性质解答即可．
【详解】∵∠A=54°，∠B=48°，
∴∠ACB=180°﹣54°﹣48°=78°，
∵CD平分∠ACB交AB于点D，
∴∠DCB=×78°=39°，
∵DE∥BC，
∴∠CDE=∠DCB=39°，
故选C．
【点睛】本题考查了三角形内角和定理、角平分线的定义、平行线的性质等，解题的关键是熟练掌握和灵活运用根据三角形内角和定理、角平分线的定义和平行线的性质．
8．（2022·西安建筑科技大学附属中学）如图，∠B=∠C，则∠ADC与∠AEB的大小关系是( )

A．∠ADC>∠AEB B．∠ADC