- 第01讲 二次根式的运算专题复习-【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第03讲 一元二次方程几何应用之动点问题专题复习 -【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
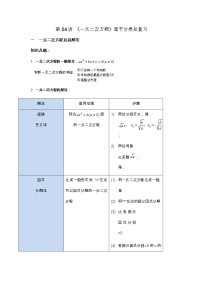
- 第04讲 一元二次方程章节分类总复习 -【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第05讲 平行四边形存在性问题专题复习 -【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
- 第06讲 平行四边形单元整体分类总复习 -【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版) 试卷 0 次下载
第02讲 二次根式章节分类总复习 -【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版)
展开第02讲 《二次根式》章节分类总复习
考点一 二次根式有意义的条件
知识点睛:
- 二次根式的定义:非负数a的算术平方根叫做二次根式
☆:二次根式的判断不需要化简,直接根据定义判断即可,
易错类型:因为,误认为不是二次根式
- 二次根式有意义的条件
中a叫做被开方数,其中二次根式有意义的条件就是a≥0;
☆1:当二次根式和分式结合时,要注意分式的分母≠0
☆2:的双重非负性
;故有:前无“-”,本身值不可能是负的
类题训练
1.下列式子,哪些是二次根式,哪些不是二次根式:,,,(x>0),,,﹣,,(x≥0,y≥0).
2.(2022春•下城区期末)已知二次根式,当x=1时,此二次根式的值为( )
A.2 B.±2 C.4 D.±4
3.(2022春•阳谷县期末)已知是整数,则正整数n的最小值是
4.(2022秋•普陀区期中)若是二次根式,那么x的取值范围是 .
5.(2022春•余杭区期中)当x= 时,的值最小.
6.已知二次根式.
(1)求x的取值范围;
(2)求当x=﹣2时,二次根式的值;
(3)若二次根式的值为零,求x的值.
7.已知x、y为实数,且满足,求5x+|2y﹣1|﹣的值.
考点二 二次根式相关概念
知识点睛:
- 最简二次根式:满足以下2个条件的二次根式成为最简二次根式
①被开方数的因数是整数,因式是整式;②不含开的尽方的因数或因式
☆:判断最简二次根式,被开方数的字母部分次数最高为1次,且不含分母
二次根式的运算,最后结果都要求必须化为最简二次根式
- 同类二次根式:所含被开方数相同的最简二次根式叫做同类二次根式
类题训练
1.(2022秋•桐柏县期中)下列二次根式中的最简二次根式是( )
A. B. C. D.
2.把下列根式化成最简二次根式.
(1)5
(2)6
(3)(a>0)
(4)(n<0)
3.(2022春•岳麓区校级期末)下列式子能与合并的是( )
A. B. C. D.
4.如果最简二次根式与2是同类二次根式,则a= .
考点三 二次根式的运算
知识点睛:
二次根式乘法公式:
二次根式除法公式:
类题训练
1.(2022秋•拱墅区期中)下列计算正确的是( )
A. B. C. D.
2.(2022秋•宝山区校级月考)把根号外面的式子移到根号内,则x= .
3.(2022春•诸暨市月考)已知:2、3、y是一个三角形的三条边,则|y﹣1|+的化简结果 .
4.(2022春•新县期末)已知|2019﹣a|+=a,求a﹣20192的值是 .
5.(2022秋•普陀区校级期中)下列结论正确的是( )
A.的有理化因式可以是
B.
C.不等式(2﹣)x>1的解集是x>﹣(2+)
D.是最简二次根式
6.(2022春•九龙坡区校级月考)已知x+y=﹣5,xy=4,则的值是( )
A. B. C. D.
7.(2022春•高青县期末)已知x=+2,则代数式x2﹣x﹣2的值为( )
A.9 B.9 C.5 D.5
8.(2022秋•南岸区校级期中)已知a,b是两个连续整数,若a<<b,则+= .
9.(2022•诸城市三模)已知a=+1,b=﹣1,则a3b﹣ab3= .
10.(2022春•杭州期末)若a=+1,b=﹣1,则a2﹣ab+b2= .
11.(2022秋•市北区校级期中)计算:
(1)﹣;
(2)3﹣+7;
(3)(﹣)×﹣3;
(4)(+)(﹣)﹣(+1)2.
(5);
(6).
考点四 二次根式的化简求值及简单应用
知识点睛:
1.二次根式的化简求值解题步骤:
①根据实数的混合运算法则和二次根式的性质公式将所给代数式化到最简
②将所给字母的值带入计算
☆化简求值问题所得结果必须是最简二次根式或者实数
2.图形的坡比:
直线AB的坡比i=
类题训练:
1.先化简,再求值:,其中a=,b=5+2.
2.(2022秋•鄞州区月考)已知a=.
(1)求a2﹣4a+4的值;
(2)化简并求值:.
3.(2022秋•奉贤区校级期中)若,则x的取值范围是( )
A. B. C. D.x<
4.(2022秋•余杭区期中)如图是单位长度为1的正方形网格,点A,B,C都在格点上,则点C到AB所在直线的距离为( )
A. B. C. D.
5.(2022秋•普陀区校级月考)已知a+b=﹣8,ab=1,则值为 .
6.(2018春•台州期中)如图,在矩形ABCD中无重叠放入面积分别为8cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )
A.4cm2 B.(8﹣12)cm2 C.(4﹣8)cm2 D.(4+12)cm2
- 已知一个直角三角形的周长是4+,斜边上的中线长是2,则这个三角形的面积是( )
A.5 B. C. D.1
8.(2022秋•隆昌市校级月考)先阅读下面的解题过程,然后再解答:
形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,
即,,
则有:.
(1)根据上述方法化简:
①= ;
②= ;
(2)已知,则4x2+4x﹣2022= .
9.(2022春•长丰县期末)观察下列等式:
第一个等式:,
第二个等式:,
第三个等式:,
…
请回答下列问题:
(1)则第四个等式为 ;
(2)用含n(n为正整数)的式子表示出第n个等式为 .
10.(2020春•博白县期末)已知长方形的长a=,宽b=.
(1)求长方形的周长;
(2)求与长方形等面积的正方形的周长,并比较与长方形周长的大小关系.
11.(2020春•越城区校级月考)点P(x,y)是平面直角坐标系中的一点,点A(1,0)为x轴上的一点.
(1)用二次根式表示点P与点A的距离;
(2)当x=4,y=时,连接OP、PA,求PA+PO;
(3)若点P位于第二象限,且满足函数表达式y=x+1,求+的值.
12.(2022秋•南岸区校级期中)某居民小区有块形状为长方形ABCD的绿地,长方形绿地的长BC为8米,宽AB为米,现要在长方形绿地中修建一个长方形花坛(即图中阴影部分),长方形花坛的长为+1米,宽为﹣1米.
(1)长方形ABCD的周长是多少?(结果化为最简二次根式)
(2)除去修建花坛的地方.其它地方全修建成通道,通道上要铺上造价为6元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)
13.(2022春•西城区校级期中)(1)用“=”、“>”、“<”填空:4+3 2,1+ 2,5+5 2.
(2)由(1)中各式猜想m+n与2(m≥0,n≥0)的大小,并说明理由.
(3)请利用上述结论解决下面问题:
某园林设计师要对园林的一个区域进行设计改造,将该区域用篱笆围成矩形的花圃.如图所示,花圃恰好可以借用一段墙体,为了围成面积为200m2的花圃,所用的篱笆至少需要 m.
【坡比问题】
1.(2022秋•正定县期中)如图,AB是河堤横断面的迎水坡,堤高AC=,水平距离BC=1,则斜坡AB的坡度为( )
A. B. C.30° D.60°
2.(2022秋•东昌府区期中)如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10米,背水坡CD的坡度i=1:,则背水坡的坡长CD为( )米.
A.20 B.20 C.10 D.20
3.(2022秋•闵行区期中)一段公路路面的坡度为i=1:2.4,如果某人沿着这段公路向上行走了130米,那么此人升高了 米.
4.(2022秋•任城区校级月考)水坝的横截面是梯形ABCD,现测得坝顶DC=4m,坡面AD的坡度i为1:1,坡面BC的坡角β为60°,坝高3m,(≈1.732)求:
(1)坝底AB的长(精确到0.1);
(2)水利部门为了加固水坝,在保持坝顶CD不变的情况下降低AD的坡度(如图),使新坡面DE的坡度i为1:,原水坝底部正前方2.5m处有一千年古树,此加固工程对古树是否有影响?请说明理由.
第02讲 二次根式的运算专题复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版): 这是一份第02讲 二次根式的运算专题复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版),文件包含第02讲二次根式的运算专题复习解析版docx、第02讲二次根式的运算专题复习原卷版docx等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
第01讲 二次根式单元分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版): 这是一份第01讲 二次根式单元分类总复习-2023-2024学年八年级数学下册重难点及章节分类精品讲义(浙教版),文件包含第01讲二次根式单元分类总复习原卷版docx、第01讲二次根式单元分类总复习解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
第12讲 反比例函数单元整体分类总复习-【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版): 这是一份第12讲 反比例函数单元整体分类总复习-【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版),文件包含第12讲反比例函数单元整体分类总复习-专题突破2022-2023学年八年级数学下学期重难点及章节分类精品讲义浙教版解析版docx、第12讲反比例函数单元整体分类总复习-专题突破2022-2023学年八年级数学下学期重难点及章节分类精品讲义浙教版原卷版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。