第08讲 特殊平行四边形单元整体分类总复习-【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版)

这是一份第08讲 特殊平行四边形单元整体分类总复习-【专题突破】2022-2023学年八年级数学下学期重难点及章节分类精品讲义(浙教版)，文件包含第8讲特殊平行四边形单元整体分类总复习-专题突破2022-2023学年八年级数学下学期重难点及章节分类精品讲义浙教版解析版docx、第8讲特殊平行四边形单元整体分类总复习-专题突破2022-2023学年八年级数学下学期重难点及章节分类精品讲义浙教版原卷版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
矩形的判定方法：
①有一个角是直角的平行四边形是矩形; ②有三个角是直角的四边形是矩形;
③四个角都相等的四边形是矩形; ④对角线相等的平行四边形是矩形;
⑤对角线相等且互相平分的四边形是矩形.
矩形的性质
①矩形的对边平行且相等; ②矩形的四个角都是直角;
③矩形的对角线相等且互相平分; ④矩形既是轴对称图形，又是中心对称图形。
类题训练
1．矩形具有而平行四边形不一定具有的性质是（ ）
A．对边相等 B．对角相等C．对角线相等 D．对角线互相平分
2.如图，已知点P是矩形ABCD内一点（不含边界），设∠PAD＝θ1，∠PBA＝θ2，∠PCB＝θ3，∠PDC＝θ4，若∠APB＝80°，∠CPD＝50°，则（ ）
A．（θ1+θ4）﹣（θ2+θ3）＝30°B．（θ2+θ4）﹣（θ1+θ3）＝40°
C．（θ1+θ2）﹣（θ3+θ4）＝70°D．（θ1+θ2）+（θ3+θ4）＝180°
3．如图，在矩形ABCD中，AB＝6，BC＝8，过对角线交点O作EF⊥AC交AD于点E，交BC于点F，则DE的长是（ ）
A．1B．C．2D．

第3题 第4题 第5题
4．如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE＝2，PF＝8．则图中阴影部分的面积为（ ）
A．10B．12C．16D．18
5.如图，在矩形ABCD中，AB＝2，BC＝3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（ ）
A．B．C．D．
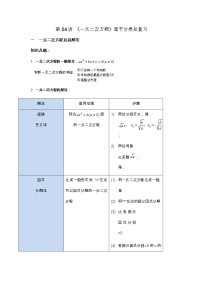
6.如图所示，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE＝15°，则下面的结论：
①△ODC是等边三角形；②BC＝2AB；③∠AOE＝135°；④S△AOE＝S△COE，
其中正确结论有（ ）
A．1个B．2个C．3个D．4个
第6题 第7题 第8题
7.如图，在矩形ABCD中，AB＝3，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为 ．
8.如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是 ．
9．如图是一张长方形纸片ABCD，已知AB＝8，AD＝7，E为AB上一点，AE＝5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是 ．
10．矩形ABCD与矩形CEFG如图放置，点B、C、E共线，点C、D、G共线，连接AF，取AF的中点H，连接GH．若BC＝EF＝3，CD＝CE＝1，则GH＝ ．
11．陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件．在交付客户之前，陈师傅需要对4个零件进行检测．根据零件的检测结果，图中有可能不合格的零件是（ ）
A．B．C．D．
12．如图，四边形ABCD是平行四边形，两条对角线交于点O，下列条件中，不能判定平行四边形ABCD为矩形的是（ ）
A．∠ABC＝∠BCDB．∠ABC＝∠ADC
C．AO＝BOD．AO＝DO
13．如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）
A．AB∥DC B．AC＝BD C．AC⊥BD D．AB＝DC
14．如图，在四边形ABCD中，∠B＝∠C．点E、F、G分别在边AB、BC、CD上，AE＝GF＝GC．
（1）求证：四边形AEFG是平行四边形；
（2）当∠FGC与∠EFB满足怎样的关系时，四边形AEFG是矩形．请说明理由．
15．如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG．
（1）求证：△ABE≌△CDF；
（2）当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．
考点二 菱形的判定与性质
知识点睛：
1.菱形的判定方法：
①有一组邻边相等的平行四边形是菱形； ②四条边相等的四边形是菱形；
③对角线互相垂直的平行四边形是菱形； ④对角线互相垂直平分的四边形是菱形。
2.菱形的性质
①菱形的四条边都相等； ②菱形的对角线互相垂直平分且每条对角线平分一组对角；
③菱形既是轴对称图形又是中心对称图形； ④菱形的面积等于对角线乘积的一半。
３．应熟练掌握菱形在边、角、对角线等方面的性质，菱形的问题经常可转化为直角三角形的问题。
类题训练
1．如图，在∠MON的两边上分别截取OA、OB，使OA＝OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB＝2cm，四边形OACB的面积为4cm2．则OC的长为（ ）
A．2B．3C．4D．5
第1题 第2题 第3题 第4题
2．如图，平行四边形ABCD中，∠A＝110°，AD＝DC．E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠PEF＝（ ）
A．35°B．45°C．50°D．55°
3．如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是 ，依据是 ．
4．如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD（不完全重合），则四边形ABCD面积的最大值是（ ）
A．15B．16C．19D．20
5．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（ ）
A．B．C．5D．4
6．如图，▱ABCD中，对角线AC、BD相交于点O，AD＝AC，M、N、P分别是OA、OB、CD的中点，下列结论：
①CN⊥BD；
②MN＝NP；
③四边形MNCP是菱形；
④ND平分∠PNM．
其中正确的有（ ）
A．1 个B．2 个C．3 个D．4 个
7．如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，
（1）求证：∠DHO＝∠DCO．
（2）若OC＝4，BD＝6，求菱形ABCD的周长和面积．
8．（2020•易门县二模）如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作平行四边形ECFG，如图1所示．
（1）证明平行四边形ECFG是菱形；
（2）若∠ABC＝120°，连接BG、CG、DG，如图2所示，
①求证：△DGC≌△BGE；
②求∠BDG的度数．
（3）若∠ABC＝90°，AB＝8，AD＝14，M是EF的中点，如图3所示，求DM的长．
考点三 正方形的判定与性质
知识点睛：
1.正方形的判定方法：
①有一组邻边相等，并且有一个角是直角的平行四边形是正方形；
②有一组邻边相等的矩形是正方形； ③有一个角是直角的菱形是正方形；
④对角线相等且互相平分的四边形是正方形。
2.正方形的性质
正方形具有矩形、菱形的一切性质
平行四边形与特殊平行四边形间的转化关系：
类题训练
1．如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（ ）
A．45°B．55°C．60°D．75°
第1题 第2题 第3题
2．如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC＝2：1，则线段CH的长是（ ）
A．3B．4C．5D．6
3．如图，在四边形ABCD中，∠ADC＝∠ABC＝90°，AD＝CD，DP⊥AB于P．若四边形ABCD的面积是18，则DP的长是 ．
4．如图，点P的坐标为（4，4），点A，B分别在x轴，y轴的正半轴上运动，且∠APB＝90°，连接AB，OP，下列结论：
①PA＝PB；
②若OP与AB的交点恰好是AB的中点，则四边形OAPB是正方形；
③四边形OAPB的面积与周长为定值；
④AB＞OP．
其中正确的结论是（ ）
A．①②B．①②③C．①③④D．①②④
5．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（ ）
A．4个B．3个C．2个D．1个
6．如图，在梯形ABCD中，AD∥BC（BC＞AD），∠D＝90°，BC＝CD＝12，∠ABE＝45°，若AE＝10．求CE的长度．
7．如图，正方形ABCD中，AB＝4，点E是对角线AC上的一点，连接DE．过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩形DEFG，连接AG．
（1）求证：矩形DEFG是正方形；
（2）求AG+AE的值；
（3）若F恰为AB中点，连接DF交AC于点M，请直接写出ME的长．
四边形综合问题训练
1．如图，在矩形ABCD中，AB＝2，BC＝4，对角线AC，BD相交于点O，OE⊥AC交BC于点F，EF⊥BD于点F，则OE+EF的值为（ ）
B．2C．D．2
第1题 第2题 第3题
2．如图，在直角三角形ABC中，∠ACB＝90°，AC＝3，BC＝4，点M是边AB上一点（不与点A，B重合），作ME⊥AC于点E，MF⊥BC于点F，若点P是EF的中点，则CP的最小值是（ ）
A．1.2B．1.5C．2.4D．2.5
3．如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是 ．
4．如图，矩形ABCD中，AB＝4，BC＝2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为 ．
5.如图，矩形ABCD中，AB＞AD，AN平分∠DAB，DM⊥AN于点M，CN⊥AN于点N，G为MN的中点，GH⊥MN交CD于点H，且DM＝a，GH＝b，则CN的值为（用含a、b的代数式表示）（ ）
A．2a+bB．a+2b
C．a+bD．2a+2b
6．如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE，设AC＝10，BD＝24，则OE的长为 ．
7．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（ ）
B．C．5D．4
8．如图，已知AB＝8，P为线段AB上的一个动点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，∠DAP＝60°．M，N分别是对角线AC，BE的中点．当点P在线段AB上移动时，点M，N之间的距离最短为 （结果留根号）．
9．如图，边长一定的正方形ABCD，Q为CD上一个动点，AQ交BD于点M，过M作MN⊥AQ交BC于点N，作NP⊥BD于点P，连接NQ，下列结论：①AM＝MN；②MP＝BD；③BN+DQ＝NQ；④为定值．其中一定成立的是（ ）
A．①②③B．①②④
C．②③④D．①②③④
10．【猜想】如图1，在平行四边形ABCD中，点O是对角线AC的中点，过点O的直线分别交AD．BC于点E．F．若平行四边形ABCD的面积是8，则四边形CDEF的面积是 ．
【探究】如图2，在菱形ABCD中，对角线相交于点O，过点O的直线分别交AD，BC于点E，F，若AC＝5，BD＝10，求四边形ABFE的面积．
【应用】如图3，在Rt△ABC中，∠BAC＝90°，延长BC到点D，使DC＝BC，连接AD，若AC＝3，AD＝2，则△ABD的面积是 ．