专题1.45 全等三角形几何模型-8字模型（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（浙教版）

这是一份专题1.45 全等三角形几何模型-8字模型（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（浙教版），共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
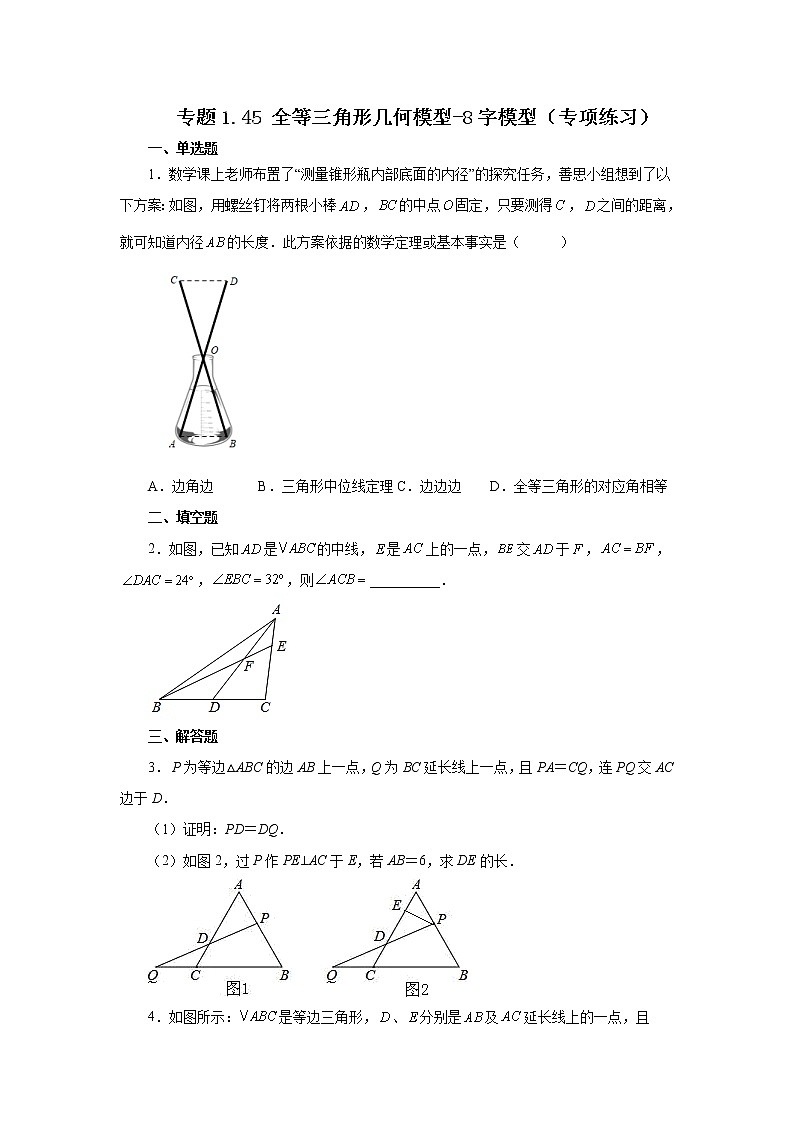
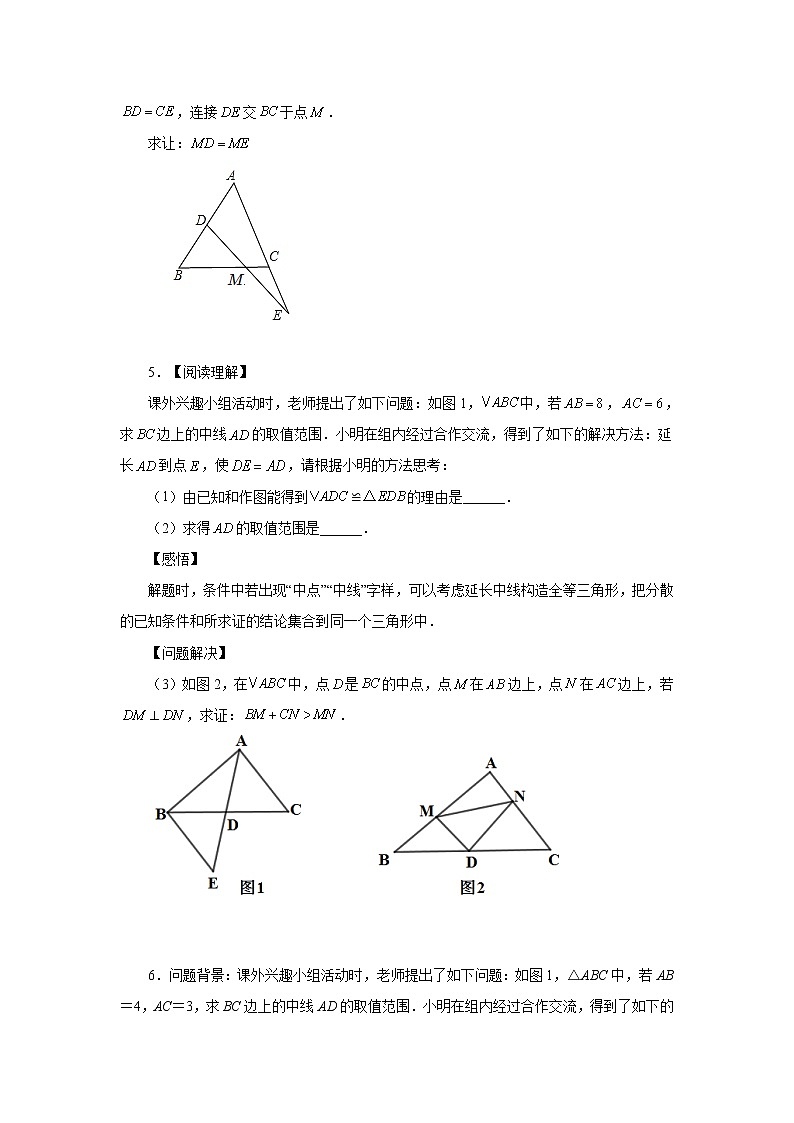
专题1.45 全等三角形几何模型-8字模型（专项练习）一、单选题1．数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务，善思小组想到了以下方案：如图，用螺丝钉将两根小棒，的中点固定，只要测得，之间的距离，就可知道内径的长度．此方案依据的数学定理或基本事实是（       ）A．边角边 B．三角形中位线定理 C．边边边    D．全等三角形的对应角相等二、填空题2．如图，已知是的中线，是上的一点，交于，，，，则__________．三、解答题3． P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA＝CQ，连PQ交AC边于D．（1）证明：PD＝DQ．（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．4．如图所示：是等边三角形，、分别是及延长线上的一点，且，连接交于点．求让： 5．【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，中，若，，求边上的中线的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长到点，使，请根据小明的方法思考：（1）由已知和作图能得到≌的理由是______．（2）求得的取值范围是______．【感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】（3）如图2，在中，点是的中点，点在边上，点在边上，若，求证：．  6．问题背景：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝4，AC＝3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，则得到△ADC≌△EDB，小明证明△BED≌△CAD用到的判定定理是：　    （用字母表示）；问题解决：小明发现：解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．请写出小明解决问题的完整过程；拓展应用：以△ABC的边AB，AC为边向外作△ABE和△ACD，AB＝AE，AC＝AD，∠BAE＝∠CAD＝90°，M是BC中点，连接AM，DE．当AM＝3时，求DE的长．               7．△ABC、△DPC都是等边三角形．(1)如图1，求证：AP＝BD；(2)如图2，点P在△ABC内，M为AC的中点，连PM、PA、PB，若PA⊥PM，且PB＝2PM．①求证：BP⊥BD；②判断PC与PA的数量关系并证明．  8．如图1，在△ABC中，∠BAC＝90°，AB＝AC，点D在边AC上，CD⊥DE，且CD＝DE，连接BE，取BE的中点F，连接DF．(1)请直接写出∠ADF的度数及线段AD与DF的数量关系；(2)将图1中的△CDE绕点C按逆时针旋转，①如图2，（1）中∠ADF的度数及线段AD与DF的数量关系是否仍然成立？请说明理由；②如图3，连接AF，若AC＝3，CD＝1，求S△ADF的取值范围．     参考答案1．A【分析】根据O是AD与BC的中点，得到OA=OD，OB=OC，根据∠AOB=∠DOC，推出△AOB≌△DOC，是SAS．解：∵O是AD与BC的中点，∴OA=OD，OB=OC，∵∠AOB=∠DOC，∴△AOB≌△DOC(SAS)．故选A．【点拨】本题考查了测量原理，解决此类问题的关键是根据测量方法和工具推导测量原理．2．100°【分析】延长AD到M，使得DM=AD，连接BM，证△BDM≌△CDA（SAS），得BM=AC=BF，∠M=∠DAC=24°，∠C=∠DBM，再证△BFM是等腰三角形，求出∠MBF的度数，即可解决问题．解：如图，延长AD到M，使得DM=AD，连接BM，如图所示：在△BDM和△CDA中，，∴△BDM≌△CDA（SAS），∴BM=AC=BF，∠M=∠DAC=24°，∠C=∠DBM，∵BF=AC，∴BF=BM，∴∠M=∠BFM=24°，∴∠MBF=180°-∠M-∠BFM=132°，∵∠EBC=32°，∴∠DBM=∠MBF-∠EBC=100°，∴∠C=∠DBM=100°，故答案为：100°．【点拨】本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．3．（1）证明见分析；（2）DE＝3．【分析】（1）过点P作PF∥BC交AC于点F；证出△APF也是等边三角形，得出AP=PF=AF=CQ，由AAS证明△PDF≌△QDC，得出对应边相等即可；（2）过P作PF∥BC交AC于F．同（1）由AAS证明△PFD≌△QCD，得出对应边相等FD=CD，证出AE+CD=DEAC，即可得出结果．解：（1）如图1所示，点P作PF∥BC交AC于点F．∵△ABC是等边三角形，∴△APF也是等边三角形，AP=PF=AF=CQ．∵PF∥BC，∴∠PFD=∠DCQ．在△PDF和△QDC中，，∴△PDF≌△QDC（AAS），∴PD=DQ；（2）如图2所示，过P作PF∥BC交AC于F．∵PF∥BC，△ABC是等边三角形，∴∠PFD=∠QCD，△APF是等边三角形，∴AP=PF=AF．∵PE⊥AC，∴AE=EF．∵AP=PF，AP=CQ，∴PF=CQ．在△PFD和△QCD中，，∴△PFD≌△QCD（AAS），∴FD=CD．∵AE=EF，∴EF+FD=AE+CD，∴AE+CD=DEAC．∵AC=6，∴DE=3．   【点拨】本题考查等边三角形的判定与性质、全等三角形的判定（AAS）与性质、平行线的性质，熟练掌握等边三角形的性质，解题的关键是掌握等边三角形的判定与性质、全等三角形的判定（AAS）与性质、平行线的性质，熟练掌握等边三角形的性质．4．见详解【分析】过点D作DE∥AC，交BC于点E，根据等边三角形和平行线的性质得∠MDE=∠MEC，DE=CE，从而证明∆EMD≅∆CME，进而即可得到结论．解：过点D作DE∥AC，交BC于点E，∵是等边三角形，∴∠B=∠ACB=60°，∵DE∥AC，∴∠DEB=∠ACB=60°，∠MDE=∠MEC，∴是等边三角形，∴BD=DE，∵，∴DE=CE，又∵∠EMD=∠CME，∴∆EMD≅∆CME，∴．【点拨】本题主要考查等边三角形的性质和判定定理以及全等三角形的判定和性质定理，添加辅助线，构造等边三角形和全等三角形，是解题的关键．5．（1）；（2）；（3）见分析【分析】（1）根据AD=DE，∠ADC=∠BDE，BD=DC推出△ADC和△EDB全等即可；（2）根据全等得出BE=AC=6，AE=2AD，由三角形三边关系定理得出8-6＜2AD＜8+6，求出即可；（3）延长至点，使，连接、，证明≌，得到，根据三角形三边关系解答即可．（1）解：∵在△ADC和△EDB中，，∴△ADC≌△EDB（SAS），故答案为：SAS；（2）解：∵由（1）知：△ADC≌△EDB，∴BE=AC=6，AE=2AD，∵在△ABE中，AB=8，由三角形三边关系定理得：8-6＜2AD＜8+6，∴1＜AD＜7，故答案为：1＜AD＜7．（3）证明：延长至点，使，连接、，如图所示：∵点是的中点，∴．在和中， ，∴≌，∴，∵，，∴，在中，由三角形的三边关系得：，∴．【点拨】本题是三角形综合题，主要考查了三角形的中线，三角形的三边关系定理，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．6．问题背景： SAS；问题解决：完整过程见分析；拓展应用： DE＝6．【分析】问题背景：先判断出BD=CD，由对顶角相等∠BDE=∠CDA，进而得出△ADC≌△EDB（SAS）；问题解决：先证明△ADC≌△EDB（SAS），得出BE=AC=3，最后用三角形三边关系即可得出结论；拓展应用：如图2，延长AM到N，使得MN=AM，连接BN，同（1）的方法得出△BMN≌△CMA（SAS），则BN=AC，进而判断出∠ABN=∠EAD，进而判断出△ABN≌△EAD，得出AN=ED，即可求解．解：问题背景：如图1，延长AD到点E，使DE＝AD，连接BE，∵AD是△ABC的中线，∴BD＝CD，在△ADC和△EDB中，，∴△ADC≌△EDB（SAS），故答案为：SAS；问题解决：如图1，延长AD到点E，使DE＝AD，连接BE，∵AD是△ABC的中线，∴BD＝CD，在△ADC≌△EDB中，，∴△ADC≌△EDB（SAS），∴BE＝AC，在△ABE中，AB﹣BE＜AE＜AB+BE，∵AB＝4，AC＝3，∴4﹣3＜AE＜4+3，即1＜AE＜7，∵DE＝AD，∴AD＝AE，∴＜AD＜；拓展应用：如图2，延长AM到N，使得MN＝AM，连接BN，由问题背景知，△BMN≌△CMA（SAS），∴BN＝AC，∠CAM＝∠BNM，∴AC//BN，∵AC＝AD， ∴BN＝AD，∵AC//BN，∴∠BAC+∠ABN＝180°，∵∠BAE＝∠CAD＝90°，∴∠BAC+∠EAD＝180°，∴∠ABN＝∠EAD，在△ABN和△EAD中，，∴△ABN≌△EAD（SAS），∴AN＝DE，∵MN＝AM，∴DE＝AN＝2AM，∵AM＝3，∴DE＝6．【点拨】此题考查了全等三角形的判定和性质，平行线的判定与性质，补角的性质，掌握倍长中线法，构造全等三角形是解本题的关键．7．(1)证明过程见分析；(2)①证明过程见分析；②PC=2PA，理由见分析．【分析】（1）证明△BCD≌△ACP（SAS），可得结论；（2）①如图2中，延长PM到K，使得MK=PM，连接CK．证明△AMP≌△CMK（SAS），推出MP=MK，AP=CK，∠APM=∠K=90°，再证明△PDB≌△PCK（SSS），可得结论；②结论：PC=2PA．想办法证明∠DPB=30°，可得结论．(1)证明：如图1中，∵△ABC，△CDP都是等边三角形，∴CB=CA，CD=CP，∠ACB=∠DCP=60°，∴∠BCD=∠ACP，在△BCD和△ACP中，，∴△BCD≌△ACP（SAS），∴BD=AP；(2)证明：如图2中，延长PM到K，使得MK=PM，连接CK．∵AP⊥PM，∴∠APM=90°，在△AMP和△CMK中，，∴△AMP≌△CMK（SAS），∴MP=MK，AP=CK，∠APM=∠K=90°，同法可证△BCD≌△ACP，∴BD=PA=CK，∵PB=2PM，∴PB=PK，∵PD=PC，∴△PDB≌△PCK（SSS），∴∠PBD=∠K=90°，∴PB⊥BD．②解：结论：PC=2PA．∵△PDB≌△PCK，∴∠DPB=∠CPK，设∠DPB=∠CPK=x，则∠BDP=90°-x，∵∠APC=∠CDB，∴90°+x=60°+90°-x，∴x=30°，∴∠DPB=30°，∵∠PBD=90°，∴PD=2BD，∵PC=PD，BD=PA，∴PC=2PA．【点拨】本题属于三角形综合题，考查了全等三角形的判定和性质，等边三角形的性质，直角三角形30°角的性质等知识，解题的关键是学会添加常用辅助线，关注全等三角形解决问题．8．(1)∠ADF=45°，AD=DF；(2)①成立，理由见分析；②1≤S△ADF≤4.【分析】（1）延长DF交AB于H，连接AF，先证明△DEF≌△HBF，得BH=CD，再证明△ADH为等腰直角三角形，利用三线合一及等腰直角三角形边的关系即可得到结论；（2）①过B作DE的平行线交DF延长线于H，连接AH、AF，先证明△DEF≌△HBF，延长ED交BC于M，再证明∠ACD=∠ABH，得△ACD≌△ABH，得AD=AH，等量代换可得∠DAH=90°，即△ADH为等腰直角三角形，利用三线合一及等腰直角三角形边的关系即可得到结论；②先确定D点的轨迹，求出AD的最大值和最小值，代入S△ADF=求解即可．(1)解：∠ADF=45°，AD=DF，理由如下：延长DF交AB于H，连接AF，∵∠EDC=∠BAC=90°，∴DE∥AB，∴∠ABF=∠FED，∵F是BE中点，∴BF=EF，又∠BFH=∠DFE，∴△DEF≌△HBF，∴BH=DE，HF=FD，∵DE=CD，AB=AC，∴BH=CD，AH=AD，∴△ADH为等腰直角三角形，∴∠ADF=45°，又HF=FD，∴AF⊥DH，∴∠FAD=∠ADF=45°，即△ADF为等腰直角三角形，∴AD=DF;(2)解：①结论仍然成立，∠ADF=45°，AD=DF，理由如下：过B作DE的平行线交DF延长线于H，连接AH、AF，如图所示，则∠FED=∠FBH，∠FHB=∠EFD，∵F是BE中点，∴BF=EF，∴△DEF≌△HBF，∴BH=DE，HF=FD，∵DE=CD，∴BH=CD，延长ED交BC于M，∵BH∥EM，∠EDC=90°，∴∠HBC+∠DCB=∠DMC+∠DCB=90°，又∵AB=AC，∠BAC=90°，∴∠ABC=45°，∴∠HBA+∠DCB=45°，∵∠ACD+∠DCB=45°，∴∠HBA=∠ACD，∴△ACD≌△ABH，∴AD=AH，∠BAH=∠CAD，∴∠CAD+∠DAB=∠BAH+∠DAB=90°，即∠HAD=90°，∴∠ADH=45°，∵HF=DF，∴AF⊥DF，即△ADF为等腰直角三角形，∴AD=DF．②由①知，S△ADF=DF2=AD2，由旋转知，当A、C、D共线时，且D在A、C之间时，AD取最小值为3－1=2，当A、C、D共线时，且C在A、D之间时，AD取最大值为3+1=4，∴1≤S△ADF≤4．【点拨】本题考查了等腰直角三角形性质及判定、全等三角形判定及性质、勾股定理等知识点．构造全等三角形及将面积的最值转化为线段的最值是解题关键．遇到题干中有“中点”时，采用平行线构造出对顶三角形全等是常用辅助线．