专题2.3 图形的轴对称（巩固篇）（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（浙教版）

这是一份专题2.3 图形的轴对称（巩固篇）（专项练习）-2022-2023学年八年级数学上册基础知识专项讲练（浙教版），共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
专题2.3 图形的轴对称（巩固篇）（专项练习）
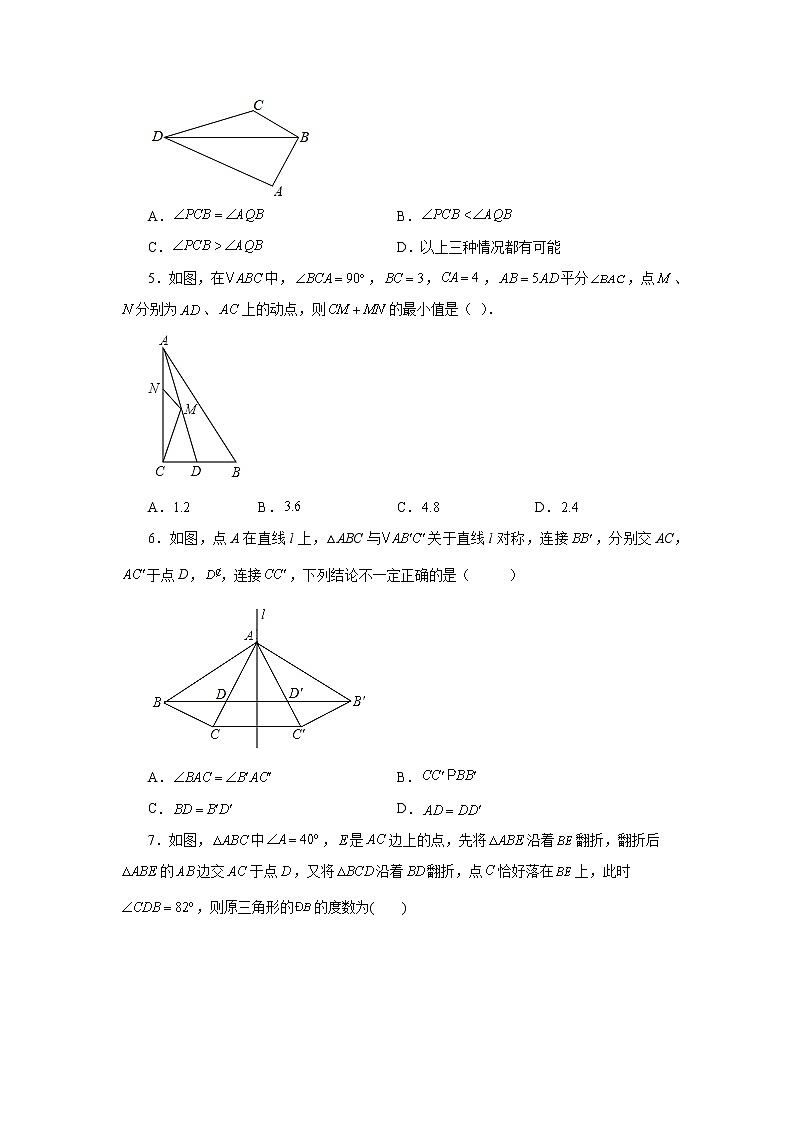
一、单选题
1．下列润滑油1ogo标志图标中，不是轴对称图形的是（       ）
A． B． C． D．
2．如图，点P是外一点，点D，E分别是两边上的点，点P关于的对称点恰好落在线段上，点P关于的对称点落在的延长线上．若，则线段的长为（       ）

A．4 B．5 C．6 D．7
3．如图，∠AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是OB、OA上的动点，记∠MPQ＝α，∠PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（　　）

A．10° B．20° C．40° D．50°
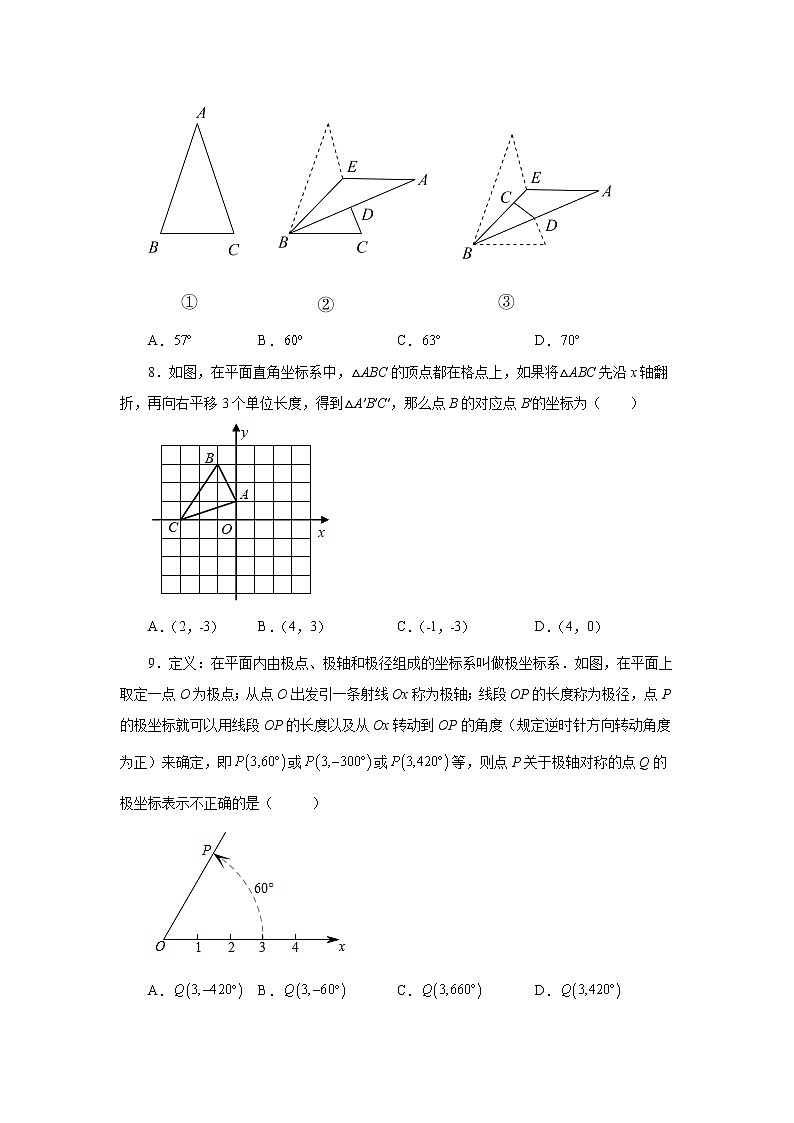
4．如图，在四边形中，请在所给的图形中进行操作：①作点A关于的对称点P：②作射线交于点Q；③连接．试用所作图形进行判断，下列选项中正确的是（       ）

A． B．
C． D．以上三种情况都有可能
5．如图，在中，，，，平分，点、分别为、上的动点，则的最小值是（ ）．

A． B． C． D．
6．如图，点A在直线l上，△ABC与关于直线l对称，连接，分别交AC，于点D，，连接，下列结论不一定正确的是（       ）

A． B．
C． D．
7．如图，中，是边上的点，先将沿着翻折，翻折后的边交于点，又将沿着翻折，点恰好落在上，此时，则原三角形的的度数为(     )

A． B． C． D．
8．如图，在平面直角坐标系中，△ABC的顶点都在格点上，如果将△ABC先沿x轴翻折，再向右平移3个单位长度，得到△A′B′C′，那么点B的对应点B′的坐标为（　　）

A．（2，﹣3） B．（4，3） C．（﹣1，﹣3） D．（4，0）
9．定义：在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O为极点；从点O出发引一条射线Ox称为极轴；线段OP的长度称为极径，点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度（规定逆时针方向转动角度为正）来确定，即或或等，则点P关于极轴对称的点Q的极坐标表示不正确的是（       ）

A． B． C． D．
10．如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝30°，分别以BE、CE为折痕进行折叠并压平，如图②，若图②中∠AED＝n°，则∠BEC的度数为（　　）度．

A．90+ B．90﹣ C．30+ D．90﹣n
二、填空题
11．等腰三角形的对称轴有_____________条.
12．如图是一个轴对称图形，AD所在的直线是对称轴，仔细观察图形，回答下列问题：
(1)、线段BO、CF的对称线段分别是_____________；
(2)、△ACE的对称三角形是______________.

13．如图，△ABC的边CB关于CA的对称线段是CB'，边CA关于CB的对称线段是CA'，连结BB'，若点A'落在BB'所在的直线上，∠ABB'＝56°，则∠ACB＝___度．

14．如图，四边形中，，，，在、上分别找一点M、N，当周长最小时，的度数是______________．

15．如图，在中，将沿直线折叠，使点B落在点D的位置，若，，则的度数是__________．

16．如图，将沿边对折，使点C落在点D处，延长到E，使，连接交于F，连接，则下列结论中：①若的周长为12，，则四边形ABDE的周长为17；②；③；④，正确的有_____________．

17．如图，中，，D、E是AC边上的点，把沿BD对折得到，再把沿BE对折得到，若恰好落在BD上，且此时，则______．

18．如图，图1是长方形纸带，将纸带沿折叠成图2，再沿折叠成图3，若图3中，则图1中的的度数是______．

三、解答题
19．已知点A（1，1），B（－1，1），C（0，4）.
（1）在平面直角坐标系中描出A，B，C三点；
（2）在同一平面内，点与三角形的位置关系有三种：点在三角形内、点在三角形边上、   点在三角形外.若点P在△ABC外，请判断点P关于y轴的对称点P′与△ABC的位置关系，直接写出判断结果.




20．已知点在内．如图，点关于射线的对称点是，点关于射线的对称点是，连接、、．
（1）若，则 ；
（2）若，连接，请说明当为多少度时，．




21．如图，已知，点E，F分别在射线，上已知点E与点B关于对称，点E与点F关于对称，求的值．




22．直角三角形ABC中，，直线l过点C．
(1) 当时，如图1，分别过点A、B作于点D，于点E．，，求DE长．
(2) 当，时，如图2，点B与点F关于直线l对称，连接BF，CF，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿向终点F运动，点M、N到达相应的终点时停止运动，过点M作于点D，过点N作于点E，设运动时间为t秒．
① ______，当N在路径上时，______．（用含t的代数式表示）
② 直接写出当与全等时t的值．






23．画图探究：
（1）如图1，点和点位于直线两侧，是直线上一点，点使的值最小．请你通过画图，在图1中找出点；
（2）如图2，点和点位于直线同侧，是直线上一点，点使的值最小．请你通过画图，在图2中找出点；
实践应用：
（3）如图3，在四边形中，，，点在边上，点在边上，点、点使的周长的值最小．请你通过画图，在图3中找出点和点并求的度数．
















24．如图，ABCD为一长方形纸片，E为BC上一点，将纸片沿AE折叠，B点落在长方形外的F点．

(1)如图1，当∠BEA＝35°时，∠FAD的度数为 ．（直接填空）
(2)如图2，连BD，若∠CBD＝25°，AFBD，求∠BAE；
(3)如图3，当AFBD时，设∠CBD＝，请你求出∠BAE的度数．（用表示）






























参考答案
1．C
【分析】
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
解：选项A、B、D能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，
选项C不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形，
故选：C．
【点拨】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．D
【分析】
利用轴对称图形的性质得出EP=EP1，DP=DP2，进而利用DE=5，得出P1D的长，即可得出P1P2的长．
解：∵点P关于CA的对称点P1恰好落在线段ED上，P点关于CB的对称点P2落在ED的延长线上，
∴EP=EP1，DP=DP2，
∵PE=2，PD=4，DE=5，
∴DP2=4，EP1=2，
∴DP1=DE−EP1=5−2=3，
则线段P1P2的长为：P1D+DP2=4+3=7，
故选：D．
【点拨】此题主要考查了轴对称图形的性质，得出EP=EP1，DP=DP2是解题关键．
3．C
【分析】
作M关于OB的对称点，N关于OA的对称点，连接交OA于Q，交OB于P，则MP＋PQ＋QN最小易知∠OPM＝∠OP＝∠NPQ，∠OQP＝∠AQ＝∠AQN，根据三角形的外角的性质和平角的定义即可得到结论．
解：如图，作M关于OB的对称点，N关于OA的对称点，连接交OA于Q，交OB于P，则MP＋PQ＋QN最小，

∴∠OPM＝∠OP＝∠NPQ，∠OQP＝∠AQ＝∠AQN，
∴∠QPN＝（180°−α）＝∠AOB＋∠MQP＝20°＋（180°−β），
∴180°−α＝40°＋（180°−β），
∴β−α＝40°，
故选：C．
【点拨】本题考查轴对称−最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题．
4．C
利用轴对称的性质以及三角形的外角的性质证明即可．
解：如图，

∵A，P关于BD对称，
∴∠AQB=∠PQB，
∵∠PCB＞∠PQB，
∴∠PCB＞∠AQB，
故选：C．
【点拨】本题考查作图-轴对称变换，解题的关键是理解题意，灵活运用所学知识解决问题．
5．D
【分析】
取点N关于AD的对称点E，由轴对称图形的性质可知MN＝ME，从而得到CM＋MN＝CM＋ME，当点C、M、E在一条直线上且CE⊥AB时，CM＋MN有最小值，最后利用面积法求得CE的值即可．
解：取点N关于AD的对称点E．

∵AD平分∠BAC，
∴点E在AB上．
∵点N与点E关于AD对称，
∴MN＝ME．
∴CM＋MN＝CM＋ME．
当CE⊥AB时，CE有最小值，即CM＋MN有最小值．
∵在Rt△ABC中，AB＝5，BC＝3，CA＝4，
∴AC•BC＝AB•CE，即5CE＝3×4，解得CE＝2.4．
故选D．
【点拨】本题主要考查的是轴对称−路径最短问题，解答本题主要应用了轴对称图形的性质、垂线段最短的性质，将CM＋MN转化为CE的长是解题的关键．
6．D
【分析】
利用轴对称的性质和全等三角形的性质逐项判断即可．
解：与关于直线对称，
，，，，，
，，即选项A、B正确；

由轴对称的性质得：，
，即，选项C正确；
由轴对称的性质得：，但不一定等于，即选项D不一定正确；
故选：D．
【点拨】本题考查了轴对称的性质、全等三角形的性质，熟练掌握轴对称的性质是解题关键．
7．C
【分析】
由折叠可得，∠BDG＝∠BDC＝82°，∠ABE＝∠A'BE＝∠A'BG，依据∠BDG是△BDF是外角，即可得到∠DBA＝∠BDG﹣∠A＝82°﹣40°＝42°，进而得到原三角形的∠B为63°．
解：如图，

由折叠可得，∠BDG＝∠BDC＝82°，∠ABE＝∠A'BE＝∠A'BG，
∵∠BDG是△BDA是外角，
∴∠DBA＝∠BDG﹣∠A＝82°﹣40°＝42°，
∴∠ABE＝∠DBE＝21°，
∴∠ABG＝3×21°＝63°，
即原三角形的∠B为63°，
故选：C．
【点拨】此题主要考查的是图形的折叠变换及三角形外角性质的应用，能够根据折叠的性质发现∠FBE＝∠ABE＝∠ABG是解答此题的关键．
8．A
【分析】
根据轴对称的性质和平移规律求得即可．
解：由坐标系可得B（﹣1，3），
将△ABC先沿x轴翻折得到B点对应点为（﹣1，﹣3），再向右平移3个单位长度，点B的对应点B'的坐标为（﹣1+3，﹣3），
即（2，﹣3），
故选：A．
【点拨】此题考查了翻折变换的性质、坐标与图形的变化--对称和平移，解题的关键是掌握点的坐标的变化规律．
9．D
【分析】
根据轴对称的定义以及给OP的角度关于Ox对称后的角度加上360°的整数倍即可．
解：∵P（3，60°）或P（3，-300°）或P（3，420°），
由点P关于极轴对称的点Q的极坐标表示点Q可得：点Q的极坐标为（3，-60°-360°=-420°）或（3， -60°）或（3，-60°+720°=660°）或（3，-60°+360°=300°）．
故选D．
【点拨】本题考查轴对称的问题，掌握轴对称的定义成为解答本题的关键．
10．B
【分析】
根据∠A=∠A′=90°，∠ABE＝30°，得出∠1=∠AEB=60°，根据平角定义可得∠DED′=180°-∠1-（∠AEB-∠DEA）=60°+n°，可得∠2=∠DED′=（n+30）°，根据平角定义可得∠BCE=180°-∠1-∠2=（90-）°即可．
解：如图，

∵∠A=∠A′=90°，∠ABE＝30°，
∴∠1=∠AEB=90°-∠ABE=60°，
∴∠DED′=180°-∠1-（∠AEB-∠DEA）=180°-60°-60°+n°=60°+n°，
∴∠2=∠DED′=（n+30）°，
∴∠BCE=180°-∠1-∠2=180°-60°-（）°=（90-）°．
故选B．
【点拨】此题考查了翻折变换的性质、矩形的性质以及直角三角形的性质；平角定义，注意数形结合思想的应用．
11．1
【分析】
依据轴对称图形的意义，即在平面内，如果一个图形沿一条直线对折，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，据此即可进行解答．
解：一般等腰三角形的对称轴有一条，即底边上的中线所在的直线．
故答案是：1．
【点拨】考查如何确定轴对称图形的对称轴条数及位置，解题关键是抓住其定义：在平面内，如果一个图形沿一条直线对折，直线两旁的部分能够完全重合，这样的图形叫做轴对称图形，这条直线为对称轴.
12．     CO、BE     △ABF
解：根据题意可得：直线AD为对称轴，则BO的对称线段为CO，CF的对称线段为BE，△ACE的对称三角形为△ABF.
考点：轴对称图形的性质
13．28°
【分析】
根据对称性可判断出BB'⊥AC，先求出∠BAC＝34°，再根据对称的性质判断△A'CB≌△ACB，最后根据∠ACA'＝2∠ACB即可求解．
解：连接BA'，AC与BB'交点为O，

∵CB关于CA的对称线段是CB'，
∴BB'⊥AC，
∵∠ABB'＝56°，
∴∠BAC＝34°，
∵边CA关于CB的对称线段是CA'，
∴△A'CB≌△ACB，
∴∠BA'C＝∠BAC＝34°，
∴∠ACA'＝2∠ACB＝56°，
∴∠ACB＝28°，
故答案为28°．
【点拨】本题主要考查了轴对称的性质及全等三角形的判定及性质，熟练掌握轴对称的性质是解题的关键．
14．128°
【分析】
分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE ，则当M、N在线段EF上时△AMN的周长最小，此时由对称的性质及三角形内角和定理、三角形外角的性质即可求得结果．
解：分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE，如图

由对称的性质得：AN=FN，AM=EM
∴∠F=∠NAD，∠E=∠MAB
∵AM+AN+MN=EM+FN+MN≥EF
∴当M、N在线段EF上时，△AMN的周长最小
∵∠AMN+∠ANM=∠E+∠MAB+∠F+∠NAD=2∠E+2∠F=2(∠E+∠F)=2(180°−∠BAD)=2×(180°−116°)=128°
故答案为：128°
【点拨】本题考查了对称的性质，两点间线段最短，三角形内角和定理与三角形外角的性质等知识，作点A关于BC、DC的对称点是本题的关键．
15．125°
【分析】
先由平行求得∠CFD，再由折叠性质得∠EFB=∠EFD，即可求解的度数．
解：∵，∠C= 70°，
∴∠DFC=∠C= 70°
由折叠性质可得∠EFB=∠EFD，
∴∠EFB +∠EFD = 180° + 70°= 250°
∴∠EFB =∠EFD= 125°．
故答案为∶ 125°．
【点拨】本题考查了折叠的性质及平行线的性质，熟练掌握平行线的性质是解题的关键．
16．①②③④
【分析】
①由题知AE＝AC，BD＝BC，可得结论正确；
②由三角形外角知∠CAB+∠DAB＝∠ADE+∠AED，又知∠CAB＝∠DAB，∠ADE＝∠AED，即可得∠CAB＝∠DAB＝∠ADE＝∠AED，即可得证结论；
③由对称知CD⊥AB，由AB∥DE可得结论；
④由③知S△ADE＝DF•DE，S△ADF＝DF•AF，证AF是中位线可得AF＝DE，即可得证结论．
解：①由图形翻折可知，AD＝AC，BD＝BC，
∵AE＝AD，
∴AE＝AC，
∴C四边形ABDE＝C△ABC+DE，
∵C△ABC＝12，DE＝5，
∴C四边形ABDE＝17，
∴①正确；
②由图形翻折知，∠CAB＝∠DAB，
∵AE＝AD，
∴∠ADE＝∠AED，
又∵∠CAB+∠DAB＝∠ADE+∠AED，
∴∠CAB＝∠DAB＝∠ADE＝∠AED，
∴ABDE，
∴②正确；
③由②知，ABDE，
由图形翻折知，CD⊥AB，
∴∠CFA＝∠CDE＝90°，
∴③正确；
④由③知，∠CFA＝∠CDE＝90°，
∴S△ADE＝DF•DE，S△ADF＝DF•AF，
∵A是EC的中点，ABDE，
∴AF是△CDE的中位线，
∴AF＝DE，
∴S△ADE＝2S△ADF，
∴④正确，
故答案为：①②③④．
【点拨】本题主要考查图形的翻折，三角形的面积，平行线的判定和性质等知识点，证明ABDE是解题的关键．
17．60°##60度
【分析】
由折叠可得，∠BEC=，∠ABD=∠DBE=∠EBC，依据∠BEC是△ABE的外角，即可得到∠ABE=∠BEC-∠A=40°，进而得到∠ABC为60°．
解：由折叠可得，∠BEC=，∠ABD=∠DBE=∠EBC，
∵∠BEC是△ABE的外角，
∴∠ABE=∠BEC-∠A=80°-40°=40°，
∴∠ABD=∠DBE=20°，
∴∠ABC=3×20°=60°，
故答案为：60°．
【点拨】此题主要考查的是图形的折叠变换及三角形外角的性质，能够根据折叠的性质发现∠ABD=∠DBE=∠EBC是解答此题的关键．
18．24°##24度
【分析】
先根据平行线的性质，设∠DEF＝∠EFB＝a，图2中根据图形折叠的性质得出∠AEF的度数，再由平行线的性质得出∠GFC，图3中根据∠CFE＝∠GFC﹣∠EFG即可列方程求得a的值．
解：∵，
∴设∠DEF＝∠EFB＝a，
图2中，∠GFC＝∠BGD＝∠AEG＝180°﹣2∠DEF＝180°﹣2a，
图3中，∠CFE＝∠GFC﹣∠EFG＝180°﹣2a﹣a＝108°．
解得a＝24°．
即∠DEF＝24°，
故答案为：24°．
【点拨】本题考查图形的翻折变换以及平行线的性质，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．
19．（1）答案见详解；（2）点P′在△ABC外.
【分析】
（1）根据点坐标直接在坐标系中描点即可；
（2）分别判断不同区域内点P的位置即可得到点P’的位置，再利用对称性判断与△ABC的位置关系.
解：（1）如图，

（2）连接AB、AC、BC,由A、B、C三点的位置得：△ABC关于y轴对称，
∵点P在△ABC外，
∴点P可在点C上方的位置，直线AB下方的位置，也可在线段BC、AC外，
若点P可在点C上方的位置，直线AB下方的位置，则点P关于y轴的对称点P′也在该位置，即点P′在△ABC外；
若点P在线段BC、AC外，则点P到y轴的距离大于线段BC、AC上的点到y轴的距离，故点P关于y轴的对称点P′到y轴的距离大于线段AC或BC上的点到y轴的距离，故点P′在△ABC外.

【点拨】此题考查轴对称图形，关于y轴对称即两个点到y轴的距离相等，根据这个特点确定点P的对称点，再用距离说明与△ABC的位置关系.
20．（1）；（2）
【分析】
（1）由题意依据轴对称可得OG=OP，OM⊥GP，即可得到OM平分∠POG，ON平分∠POH，进而得出∠GOH=2∠MON；
（2）根据题意可知当∠MON=90°时，∠GOH=180°，此时点G，O，H在同一直线上，可得GH=GO+HO=10.
解：（1）∵点P关于射线OM的对称点是G，点P关于射线ON的对称点是H，
∴OG=OP，OM⊥GP，
∴OM平分∠POG，
同理可得ON平分∠POH，
∴∠GOH=2∠MON=2×50°=100°，
故答案为：100°；
（2）∵，
∴，
当时，，
∴点，，在同一直线上，
∴.
【点拨】本题主要考查轴对称图形相关，熟练掌握角平分线性质以及轴对称图形的性质是解题的关键．
21．22.5°．
【分析】
根据轴对称的性质可得AB=AE，然后可得∠ABE=∠AEB=45°，再根据轴对称的性质可得EB=BF，BD平分∠EBF，然后求出∠FBE=45°，再根据等腰三角形的两底角相等可得∠BEF=∠BFE=67.5°，然后代入数据计算即可得解．
解：∵点E与点B关于对称，
∴，
∵，
∴，
∵点E与点F关于对称，
∴，平分，
∵，
∴，
∴，
∴
∴，
∴．
【点拨】本题主要考查了轴对称的性质、等腰直角三角形的判定与性质等知识点，熟记各性质并准确识图成为解答本题的关键．
22．(1)(2)①；②当t=秒或5秒或秒时，△MDC与△CEN全等．
【分析】
（1）根据垂直的定义得到∠DAC=∠ECB，利用AAS定理证明△ACD≌△CBE；
（2）①由即可表示利用轴对称的性质证明再利用即可得到答案； ②分点F沿F→C路径运动，点F沿C→B路径运动，点F沿B→C路径运动，点F沿C→F路径运动四种情况，根据全等三角形的判定定理列方程，再解方程即可．
(1)解：∵AD⊥直线l，
∴∠DAC+∠ACD=90°，
∵∠ACB=90°，
∴∠BCE+∠ACD=90°，
∴∠DAC=∠ECB，
，

，
∴△ACD≌△CBE（AAS）；而，，


(2)①由题意得，AM=t，
，
，
点B与点F关于直线l对称，

当N在路径上时，

故答案为：
②由轴对称的性质可知，∠BCE=∠FCE，
∵，
，∠MCD+∠CMD=90°，∠MCD+∠BCE=90°，
∴∠NCE=∠CMD，
∴当CM=CN时，△MDC与△CEN全等，
当点N 沿F→C路径运动时，8-t=6-3t，
解得，t=-1（不合题意），
当点N 沿C→B路径运动时，此时
8-t=3t-6，
解得，，
当点N 沿B→C路径运动时，此时
由题意得，8-t=18-3t，
解得，t=5，
当点N 沿C→F路径运动时，此时
由题意得，8-t=3t-18，
解得，，
综上所述，当t=秒或5秒或秒时，△MDC与△CEN全等．
【点拨】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论是解题的关键．
23．（1）见分析；（2）见分析；（3）见分析，
【分析】
（1）根据两点之间线段最短，连接，与直线相交点即是点；
（2）作点关于直线的对称点，则，连接与直线相交点即是点；
（3）分别作出点关于，的对称点，，连接分别交、于点、，根据垂直平分线的定义即可求解．
解：（1）根据两点之间线段最短，连接与直线相交点，

此时最小；
（2）作点关于直线的对称点，则

，
连接与直线相交点即是点，此时最小，即最小；
（3）如图3，分别作出点关于，的对称点，，
连接分别交、于点、，此时周长最小；

∵，，
∴，∴，
∴．
∴．
【点拨】此题考查了两点之间线段最短，轴对称的性质，熟练掌握相关性质是解题的关键．
24．(1)20° (2)57.5° (3)
【分析】
（1）先求出∠BAE的度数，然后根据翻折得出∠FAE的度数，再根据平行线的性质求出∠DAE的度数，即可得出结论；
（2）先根据AD∥BC，∠CBD=25°得出∠ADB=25°，再由AF∥BD得出∠FAD=25°，故可得出∠AGF的度数，由平行线的性质得出∠BEF的度数，根据翻折变换的性质得出∠BEA的度数，根据直角三角形的性质即可得出结论；
（3）同（2）的证明过程即可．
(1)解：由题意知ADBC，∠B=90°，
又∠BEA＝35°，
∴∠BAE=55°，
∵翻折，
∴∠FAE=∠BAE=55°，
∵ADBC，
∴∠EAD=∠BEA=35°．
∴∠FAD=∠FAE-∠EAD=20°
故答案为：20°；
(2)解∶如图2，

∵ADBC，∠CBD=25°，
∴∠ADB=25°．
∵AFBD，
∴∠FAD=25°，
∴∠AGF=90°-25°=65°．
∵ADBC，
∴∠BEF=∠AGF=65°．
∵△AEF由△AEB反折而成，
∴∠BEA=∠BEF=32.5°，
∴∠BAE=90°-32.5°=57.5°；
(3)解∶如图3，

∵ADBC，∠CBD=，
∴∠ADB=．
∵AFBD，
∴∠FAD=，
∴∠AGF=．
∵ADBC，
∴∠BEF=∠AGF=．
∵△AEF由△AEB反折而成，
∴∠BEA=∠BEF=，
∴∠BAE=．
故答案为：．
【点拨】本题考查的是平行线的性质与翻折变换，熟知图形翻折不变性的性质是解答此题的关键．