人教版八年级上册第十二章 全等三角形12.3 角的平分线的性质巩固练习

角的平分线的性质

同步精练

一、选择题（共10小题，每小题3分，共30分）

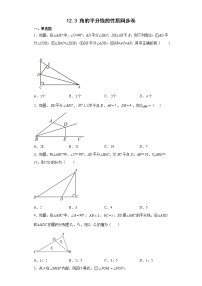
1. 如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，下列说法错误的是(    )

A．DE＝DF    B．BE＝BF   

C．∠BDE＝∠BDF    D．BE＝DE

2. 工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA，OB上分别取OC＝OD，移动角尺，使角尺两边相同的刻度分别与点C，D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线．这里构造全等三角形的依据是(　　)

A．SAS   B．ASA     C．AAS   D．SSS

3. 如图，△ABC中，∠C＝90°，AD是角平分线，DE⊥AB于点E，且BC＝5 cm，BD＝2 cm，则DE等于(    )

A．2 cm     B．3 cm    C．4 cm     D．5 cm

4. 如图，AD∥BC，∠ABC的平分线BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E.若PE＝2，则两平行线AD与BC间的距离为(    )

A．1     B．2    C．3     D．4

5. 如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B，下列结论中不一定成立的是(　　)

A．PA＝PB     B．PO平分∠APB

C．OA＝OB     D．AB垂直平分OP

6. 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直，若AD＝8，则点P到BC的距离是(　  )

A．8  B．6  C．4  D．2

7. 如图，在四边形ABCD中，∠A＝90°，AD＝3，BC＝5，对角线BD平分∠ABC，则△BCD的面积为(　　)

A．8     B．7.5     C．15    D．无法确定

8. 如图，△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P，若点P到AC的距离为2，则点P到AB的距离为(    )

A．1  B．2  C．3  D．4

9. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB交AB于点E，DF⊥AC交AC于点F.若S△ABC＝7，DE＝2，AB＝4，则AC＝(　　)

A．4  B．3  C．6  D．5

10. 如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E.有下列结论：①CD＝ED；②AC＋BE＝AB；③∠BDE＝∠BAC；④DA平分∠CDE.其中结论正确的个数是(　　)

A．1   B．2  C．3   D．4

二．填空题（共6小题，每小题4分，共24分）

11. 如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，若BC＝4，DE＝1.6，则BD的长为________．

12. 如图，AD是△ABC的角平分线．若∠B＝90°，BD＝3，则点D到AC的距离是________．

13. 如图，在四边形ABCD中，∠A＝90°，AD＝5，连接BD，BD⊥CD，∠ADB＝∠C.若P是BC边上一动点，则DP的最小值为_______．

14. 如图，在△ABC中，∠C＝90°，AD平分∠CAB交BC于点D，DE⊥AB于点E，且AB＝5 cm，AC＝3 cm，BC＝4 cm，则△DEB的周长为______．

15. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交边AC，AB于点M，N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD＝4，AB＝15，则△ABD的面积是________.

16. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝28，DE＝4，AC＝6，则AB的长是______.

三．解答题（共5小题， 46分）

17. (8分) 如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F，求证：∠B＝∠C.

18. (8分) 如图，已知：△ABC≌△A1B1C1，AD和A1D1分别是∠BAC和∠B1A1C1的角平分线．求证：AD＝A1D1.

19.(8分) 如图，在△ABC中，AC＝6，BC＝4.

(1)用直尺和圆规作∠ACB的平分线，交AB于点D(保留作图痕迹，不要求写作法)；

(2)在(1)所作的图形中，若△ACD的面积为3，求△BCD的面积．

20. (10分) 如图，AP平分∠BAC, PE⊥AC，PF⊥AB，垂足分别为E，F，点O是AP上任一点(除点A，P外).求证：OF＝OE.

21.(12分) 某同学这样画∠AOB的平分线：如图所示，分别在OA，OB上截取OC＝OD，OE＝OF，连接DE，CF，设DE，CF相交于点P，过点P作射线OP，则OP平分∠AOB.你认为他的画法正确吗？如果正确，请说明理由；如果不正确，请加以改正．

参考答案

1-5DDBDD    6-10CBBBD

11. 2.4

12. 3

13. 5

14. 6 cm

15. 30 

16. 8

17. 解：∵AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，∴DE＝DF，又∵D是BC的中点，∴BD＝CD，∴Rt△BED≌Rt△CFD(HL)，∴∠B＝∠C

18. 解：∵△ABC≌△A1B1C1，∴AB＝A1B1，∠B＝∠B1，∠BAC＝∠B1A1C1，又∵∠1＝∠BAC，∠2＝∠B1A1C1，∴∠1＝∠2，由ASA证△ABD≌△A1B1D1，∴AD＝A1D1

19. 解：(1)如图，CD即为所求．

(2)如图，过点D分别作DE⊥AC于点E，DF⊥BC于点F.∵CD是∠ACB的平分线，∴DE＝DF.∵S△ACD＝AC·DE＝3，AC＝6，∴DE＝1.∴DF＝1.∴S△BCD＝BC·DF＝×4×1＝2.

20. 解：∵AP平分∠BAC，PE⊥AC，PF⊥AB，∴∠PFA＝∠PEA＝90°，∠FAP＝∠EAP，PF＝PE，在Rt△AFP和Rt△AEP中，AP＝AP，PF＝PE，∴Rt△AFP≌Rt△AEP(HL)，∴AE＝AF，在△AFO和△AEO中，AF＝AE，∠FAO＝∠EAO，AO＝AO，∴△AFO≌△AEO(SAS)，∴OF＝OE

21. 解：这位同学的画法是正确的．理由如下：在△EOD和△FOC中，∴△EOD≌△FOC(SAS)，∴∠OEP＝∠OFP.∵OC＝OD，OE＝OF，∴CE＝DF，在△CEP和△DFP中，∴△CEP≌△DFP(AAS)，∴PE＝PF.在△EPO和△FPO中，∴△EPO≌△FPO(SSS)，∴∠EOP＝∠FOP，即OP平分∠AOB