初中1 有理数的加法法则集体备课ppt课件

这是一份初中1 有理数的加法法则集体备课ppt课件，共28页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，有理数的加法法则，答案A，有理数加法的运算律，有理数的加法等内容，欢迎下载使用。

有理数的加法法则有理数加法的运算律
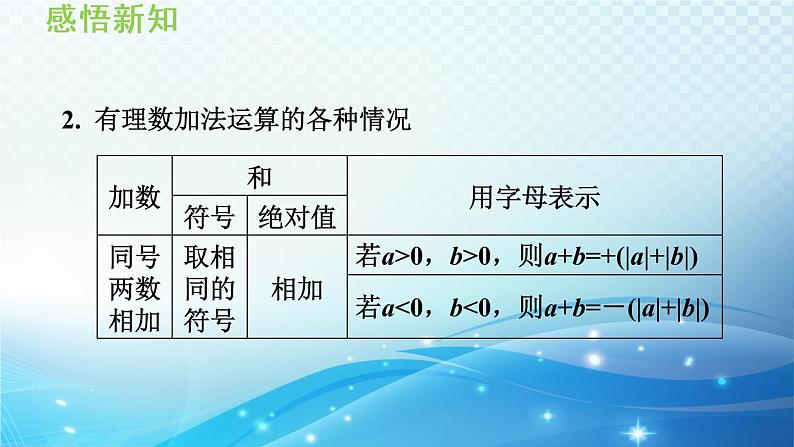
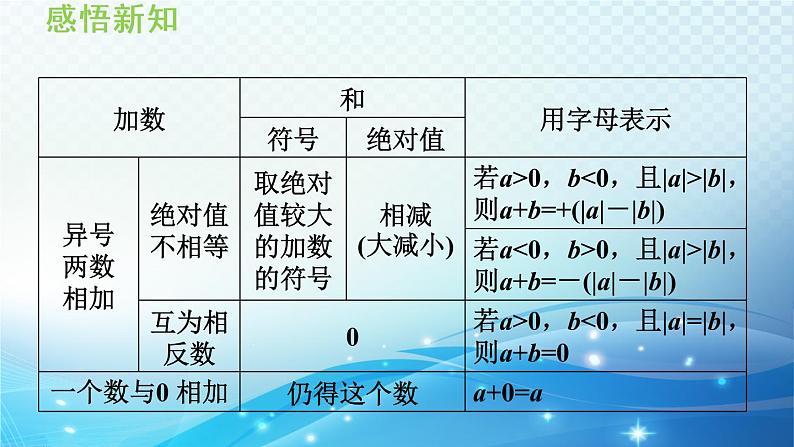
1. 有理数加法法则(1)同号两数相加，取与加数相同的正负号，并把绝对值相加；(2)绝对值不相等的异号两数相加，取绝对值较大的加数的正负号，并用较大的绝对值减去较小的绝对值；(3)互为相反数的两个数相加得零；(4)一个数与零相加，仍得这个数.
2. 有理数加法运算的各种情况
3. 有理数加法运算的步骤(1)判断加法的类型，即判断两个加数是同号，还是异号，加数中是否有0. 根据加法的类型确定用加法法则中的哪一条.(2)确定和的符号.(3)确定和的绝对值.
特别解读1. 若两个数的和为正数，则这两个数有三种可能：(1)两个都是正数；(2)一个是正数，一个是负数，且正数的绝对值大于负数的绝对值；(3)一个是正数，一个是0.
2. 若两个数的和为负数，则这两个数有三种可能：(1)两个都是负数；(2) 一个是正数，一个是负数，且负数的绝对值大于正数的绝对值；(3) 一个是负数，一个是0.
解题秘方：先确定两个数相加的类型，然后根据法则计算.
下列说法错误的是( )A. 两个有理数的和一定大于任何一个加数B. 若两个有理数的和为正数，则这两个有理数中至少有一个是正数C. 若两个有理数的和为0，则这两个有理数一定互相反数D. 异号两个有理数相加，和有可能是正数也有可能是负数或0
解题秘方：结合有理数加法法则进行辨析.
解：A. 不正确. 例如：(－3)+(－1)=－4，－4<－3,－4<－1.
2-1. 如果两个数的和是正数，那么( )A. 这两个数都是正数B. 一个为正，一个为零C. 这两个数一正一负，且正数的绝对值较大D. 这两个数必属于上面三种情况之一
2-2. 如果a+b>0，a>b，那么a 一定是( )A. 正数 B. 非正数C. 负数 D. 非负数
1. 有理数加法的运算律
2. 加法运算律的运用技巧(1)互为相反数的两个数先相加——“相反数结合法”；(2)符号相同的数先相加——“同号结合法”；(3)整数与整数、小数与小数、分母相同(或分母成倍数关系易化成同分母)的数先相加——“同形结合法”；(4)几个数相加得到整数先相加——“凑整法”.
特别提醒1. 有理数的加法运算律不但适用于两个数或三个数相加，而且适用于三个以上有理数相加.2. 利用有理数的加法交换律时，要适当加括号，如－6.6+2+(－3.4)=2+(－6.6)+(－3.4).
解题秘方：先找相反数，然后利用加法的交换律和结合律进行计算.
计算：43+(－77)+37+(－23).
解：原式=(43+37)+［(－77)+(－23)］=80+(－100)=－20.
解题秘方：先把正数、负数分别结合，再计算.
4-1. 1.6+(－2)+(－3)+14+(－15)=(6+14)+[(－2)+(－3)+(－15)]应用了( )A. 加法交换律B. 加法结合律C. 加法交换律与结合律D. 以上都不对
解题秘方：将同分母的分数通过交换结合在一起，再计算.
6-1. 用适当的方法计算：(1)0.34+(－7.6)+(－0.8)+(－0.4)+0.46；(2)(－18.35)+(+6.15)+(－3.65)+(－18.15).
解：原式＝(0.34＋0.46)＋(－0.8)＋[(－7.6)＋(－0.4)]＝0.8＋(－0.8)＋(－8)＝0＋(－8)＝－8.
原式＝[(－18.35)＋(－3.65)]＋[(＋6.15)＋(－18.15)]＝(－22)＋(－12)＝－34.