高中数学2.2 直线的方程教学设计

这是一份高中数学2.2 直线的方程教学设计，共9页。教案主要包含了做一做1，做一做2，类题通法，巩固练习1，巩固练习2，设计意图等内容，欢迎下载使用。
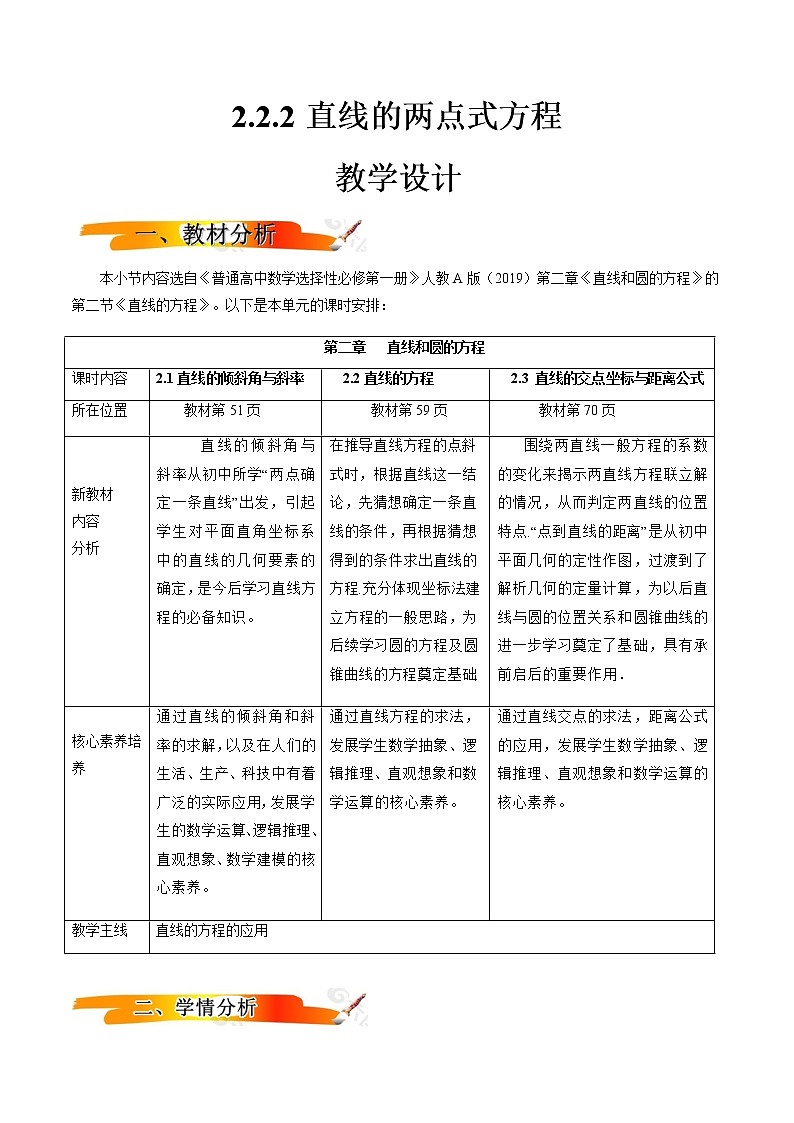
2.2.2直线的两点式方程教学设计本小节内容选自《普通高中数学选择性必修第一册》人教A版（2019）第二章《直线和圆的方程》的第二节《直线的方程》。以下是本单元的课时安排：第二章   直线和圆的方程课时内容2.1直线的倾斜角与斜率2.2直线的方程2.3 直线的交点坐标与距离公式所在位置教材第51页教材第59页教材第70页  新教材内容分析直线的倾斜角与斜率从初中所学“两点确定一条直线”出发，引起学生对平面直角坐标系中的直线的几何要素的确定，是今后学习直线方程的必备知识。 在推导直线方程的点斜式时，根据直线这一结论，先猜想确定一条直线的条件，再根据猜想得到的条件求出直线的方程.充分体现坐标法建立方程的一般思路，为后续学习圆的方程及圆锥曲线的方程奠定基础.围绕两直线一般方程的系数的变化来揭示两直线方程联立解的情况，从而判定两直线的位置特点.“点到直线的距离”是从初中平面几何的定性作图，过渡到了解析几何的定量计算，为以后直线与圆的位置关系和圆锥曲线的进一步学习奠定了基础，具有承前启后的重要作用． 核心素养培养通过直线的倾斜角和斜率的求解，以及在人们的生活、生产、科技中有着广泛的实际应用，发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。通过直线方程的求法，发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。 通过直线交点的求法，距离公式的应用，发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。教学主线直线的方程的应用 在学生亲身体验直线的两点式与截距式这两种直线方程的求法，通过典型例子的分析和学生的自主探索活动，促使学生理解数学概念、结论逐步形成的过程，从而体会蕴涵在其中的数学思想方法。 1.掌握直线的两点式方程和截距式方程，培养数学抽象的核心素养．2.会选择适当的方程形式求直线方程，提升数学运算的核心素养.3.能用直线的两点式方程与截距式方程解答有关问题，培养逻辑推理的核心素养. 重点：掌握直线方程的两点式及截距式难点：会选择适当的方程形式求直线方程 （一）新知导入某房地产公司要在荒地ABCDE上划出一块长方形土地(不改变方向)建造一幢8层的公寓，如何设计才能使公寓占地面积最大？(精确到1 m2)【提示】点P的位置由两个条件确定，一是A，P，B三点共线，二是矩形的面积最大．借助三点共线寻求x与y的关系，然后利用二次函数知识探求最大值．（二）直线的两点式方程知识点1   两点式方程【探究1】我们知道两点确定一条直线，如果已知直线上两点P1(x1，y1)，P2(x2，y2)(其中x1≠x2，y1≠y2)，那么如何求出过这两点的直线方程？【提示】因为x1≠x2，所以直线的斜率k＝，由直线的点斜式方程，得y－y1＝(x－x1)，又y1≠y2，∴上式可写为＝.于是过这两点的直线方程为＝. ◆直线的两点式方程名称已知条件示意图方程使用范围两点式P1(x1，y1)，P2(x2，y2)，其中x1≠x2，y1≠y2＝斜率存在且不为0  【点睛】1.当两点(x1,y1),(x2,y2)的直线斜率不存在(x1=x2)或斜率为0(y1=y2)时,不能用两点式方程表示,即两点式方程不能表示与坐标轴垂直的直线.2.对于两点式中的两个点,只要是直线上的两个点即可;另外,两点式方程与这两个点的顺序无关,如直线过点P1(1,1),P2(2,3),由两点式可得,也可以写成.【思考】把由直线上已知的两点坐标得到的直线方程化为整式形式(y-y1)(x2-x1)=(y2-y1)(x-x1),对两点的坐标还有限制条件吗?【做一做】(教材P66练习1改编)过点A(3,2)，B(4,3)的直线方程是(　　)A．x＋y＋1＝0　　　　 B．x＋y－1＝0C．x－y＋1＝0  D．x－y－1＝0解析：由两点式可得，过A、B的直线方程为＝，即x－y－1＝0.答案：D  知识点2  截距式方程【探究2】已知直线l与x轴的交点为A(a,0)，与y轴的交点为B(0，b)，其中a≠0，b≠0，如何求直线l的方程？【提示】将两点A(a,0)，B(0，b)的坐标代入两点式，得＝，即＋＝1.◆直线的截距式方程名称已知条件示意图方程使用范围截距式在x，y轴上的截距分别为a，b，且ab≠0＋＝1a≠0，b≠0 【做一做1】(教材P64练习1改编)过P1(2,0)，P2(0,3)两点的直线方程是(　　)A.＋＝0   B.＋＝0C.＋＝1  D.－＝1解析：由截距式，得所求直线的方程为＋＝1.答案：C【做一做2】直线l过点(-3,4),且在两坐标轴上的截距之和为12,求直线l的方程. 【解析】由于直线在两坐标轴上的截距之和为12,因此直线l在两坐标轴上的截距都存在且不过原点,故可设为截距式直线方程.设直线l的方程为=1,则a+b=12.①又直线l过点(-3,4),所以=1.②由①②解得故所求的直线方程为=1或=1,即x+3y-9=0或4x-y+16=0.（三）典型例题1.直线的两点式方程例1.三角形的三个顶点是A(－1,0)，B(3，－1)，C(1,3)，求三角形三边所在直线的方程．【分析】已知直线上两个点的坐标，可以利用两点式写出直线的方程．【解析】由两点式，直线AB所在直线方程为＝，即x＋4y＋1＝0.同理，直线BC所在直线方程为＝，即2x＋y－5＝0.直线AC所在直线方程为＝，即3x－2y＋3＝0.【类题通法】用两点式方程写出直线的方程时，要特别注意横坐标相等或纵坐标相等时，不能用两点式．已知直线上的两点坐标，也可先求出斜率，再利用点斜式写出直线方程．【巩固练习1】求经过下列两点的直线方程．(1)A(3,2)，B(4,3)；(2)A(2,1)，B(3,1)；(3)A(2,1)，B(2，－1)．【解析】(1)由两点式可得直线方程为＝，即y＝x－1.故所求的直线方程为x－y－1＝0.(2)由于A、B两点的纵坐标相等，故不能用两点式，所求的直线方程为y＝1.(3)由于A、B两点的横坐标相等，故不能用两点式，所求的直线方程为x＝2.2.直线的截距式方程例2.求经过点P(2,3)，并且在两坐标轴上截距相等的直线l的方程．【解析】法一：(1)当截距为0时，直线l过点(0,0)，(2,3)，则直线l的斜率为k＝＝，因此，直线l的方程为y＝x，即3x－2y＝0.(2)当截距不为0时，可设直线l的方程为＋＝1.∵直线l过点P(2,3)，∴＋＝1，∴a＝5，∴直线l的方程为x＋y－5＝0.综上可知，直线l的方程为3x－2y＝0或x＋y－5＝0.法二：由题意可知所求直线斜率存在，则可设y－3＝k(x－2)，且k≠0.令x＝0，得y＝－2k＋3.令y＝0，得x＝－＋2.于是－2k＋3＝－＋2，解得k＝或－1.则直线l的方程为y－3＝(x－2)或y－3＝－(x－2)，即直线l的方程为3x－2y＝0或x＋y－5＝0.【类题通法】如果题目中出现直线在两坐标轴上的“截距相等”“截距互为相反数”“在一坐标轴上的截距是另一坐标轴上截距的m倍(m>0)”等条件时，若采用截距式求直线方程，则一定要注意考虑“零截距”的情况.【巩固练习2】直线l过点P(－6,3)，且它在x轴上的截距是它在y轴上截距的3倍，求直线l的方程．【解析】(1)当直线在y轴上的截距为零时，直线过原点，可设直线l的方程为y＝kx，∵直线l过点P(－6,3)．∴3＝－6k，k＝－.∴直线l的方程为y＝－x，即x＋2y＝0.(2)当直线在y轴上的截距不为零时，由题意可设直线l的方程为＋＝1，又直线l过点P(－6,3)，∴＋＝1，解得b＝1.∴直线l的方程为＋y＝1.即x＋3y－3＝0.综上所述，所求直线l的方程为x＋2y＝0或x＋3y－3＝0.（四）操作演练  素养提升1.在x、y轴上的截距分别为－3,4的直线方程为(　　)A.＋＝1   B.＋＝1C.＋＝1  D.＋＝12.过点(5,2) ，且在y轴上的截距是在x轴上的截距的2倍的直线方程为(　　)A．2x＋y－12＝0             B．2x＋y－12＝0或2x－5y＝0C．x－2y－1＝0              D．x－2y－1＝0或2x－5y＝03.直线l过(－1，－1)，(2,5)两点，且点(1 010，b)在l上，则b的值为(　　)A．2 018  B．2 019C．2 020  D．2 0214.已知△ABC三顶点A(1,2),B(3,6),C(5,2),M为AB的中点,N为AC的中点,则中位线MN所在的直线方程为(　　)A.2x+y-8=0          B.2x-y+8=0C.2x+y-12=0          D.2x-y-12=0答案：1.A        2.B      3.D       4.A  【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。 （五）课堂小结，反思感悟 1.知识总结：  2.学生反思：（1）通过这节课，你学到了什么知识？                                                                                                                                                          （2）在解决问题时，用到了哪些数学思想？                                                                                                                                                                                 【设计意图】通过总结，让学生进一步巩固本节所学内容，提高概括能力,提高学生的数学运算能力和逻辑推理能力。完成教材：第64页  练习     第1，2，3题         第67 页   习题2.1  第4,6，7题