人教版高中数学必修第二册第七章复数课时学案

章末总结

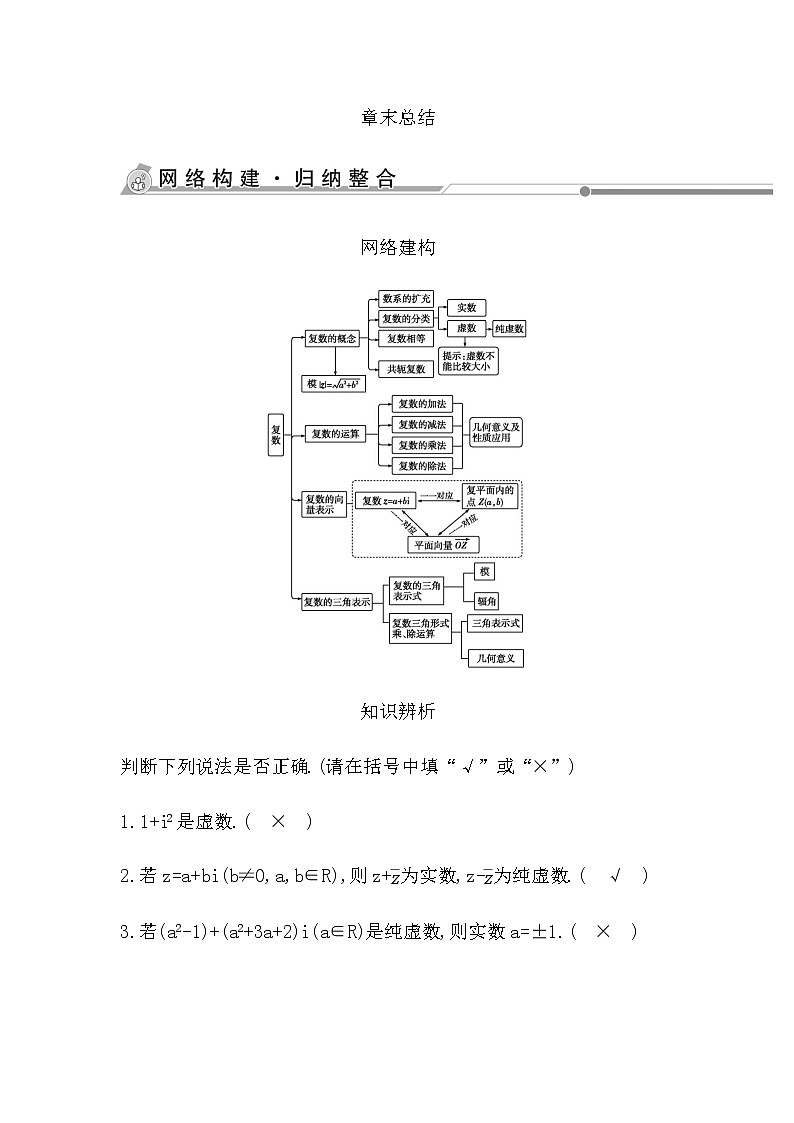
网络建构

知识辨析

判断下列说法是否正确.(请在括号中填“√”或“×”)

1.1+i2是虚数.(　×　)

2.若z=a+bi(b≠0,a,b∈R),则z+为实数,z-为纯虚数.(　√　)

3.若(a2-1)+(a2+3a+2)i(a∈R)是纯虚数,则实数a=±1.(　×　)

4.已知复数z=a+bi(a,b∈R),当a=0时,复平面内与z对应的点Z的轨迹是虚轴.(　√　)

5.-3-i的共轭复数是3+i.(　×　)

6.i是虚数单位,则i3∈S={-1,0,1}.(　×　)

7.两个复数一定不能比较大小.(　×　)

8.-3-i对应的点在第三象限.(　√　)

9.复数的除法运算中,需要分子分母同乘分子的共轭复数.(　×　)

10.满足条件0≤θ<2π的辐角叫做辐角的主值.(　√　)

11.复数三角形式的除法运算实质是模数相除,辐角相除.(　×　)

题型一　复数的有关概念

[例1](1)(多选题)已知复数z=,则下列结论中正确的是(　　)

(A)z的虚部为i

(B)=2-i

(C)|z|=

(D)z在复平面内对应的点位于第四象限

(2)若复数z=m2-1+(m2-m-2)i为纯虚数,则实数m的值为　　　　. 

解析:(1)z====2+i,

对于A,z的虚部为1,故错误;

对于B,=2-i,正确;

对于C,|z|==,正确;

对于 D, z在复平面内对应的点(2,1)位于第一象限,错误. 故选BC.

(2)因为复数(m2-1)+(m2-m-2)i为纯虚数,

所以解得m=1.

答案:(1)BC　(2)1

(2)两复数相等的充要条件是复数问题转化为实数问题的依据.

跟踪训练1: (1)若复数z=1+i(i为虚数单位),是z的共轭复数,则z2+的虚部为(　　)

(A)0 (B)-1 (C)1 (D)-2

(2)若复数是纯虚数,则实数a的值为(　　)

(A)2 (B)- (C) (D)-

解析:(1)因为z=1+i,所以=1-i,所以z2+=(1+i)2+(1-i)2=2i+(-2i)=0.故选A.

(2)因为==

是纯虚数,所以a=2.故选A.

题型二　复数的四则运算

[例2] (1)已知=2+i,则复数z等于(　　)

(A)-1+3i (B)1-3i

(C)3+i (D)3-i

(2)(多选题)数学家发现一元n次方程有n个复数根(重根按重数计),下列选项中属于方程z3-1=0的根的是(　　)

(A)+i (B)-+i

(C)--i (D)1

解析:(1)因为=2+i,

所以=(2+i)(1+i)=2+3i-1=1+3i,

所以z=1-3i.故选B.

(2)对A,当z=+i时,

z3-1=(+i) 3-1

=(+i)2·(+i)-1

=(+i+i2)·(+i)-1

=(-+i)·(+i)-1

=-+(i)2-1

=---1

=-2,

故z3-1=-2≠0,A错误;

对B,当z=-+i时,

z3-1=(-+i)3-1

=(-+i)2·(-+i)-1

=(-i+i2)·(-+i)-1

=(--i)·(-+i)-1

=-(i)2-1

=+-1

=0,

故z3-1=0,B正确;

对C,当z=--i时,

z3-1=(--i)3-1

=(--i)2·(--i)-1

=(+i+i2)·(--i)-1

=(-+i)·(--i)-1

=-(i)2-1

=+-1

=0,

故z3-1=0,C正确;

对D,显然z=1时,满足z3=1,故D正确.故选BCD.

跟踪训练2:(1)复数z=|(-i)i|+i5(i为虚数单位),则复数z的共轭复数为　　　　; 

(2)设z=+i,则|z|=　　　　. 

解析:(1)因为(-i)i=i+1,

所以|(-i)i|=|i+1|=2,

所以z=2+i5=2+i,

所以复数z的共轭复数为2-i.

(2)z=+i=+i=+i,

则|z|==.

答案:(1)2-i　(2)

题型三　复数的几何意义

[例3] 复数z满足|z+3-i|=,求|z|的最大值和最小值.

解:|z+3-i|=表示以-3+i对应的点P为圆心,

以为半径的圆,如图所示,

则|OP|=|-3+i|==2,

显然|z|max=|OA|=|OP|+=3,

|z|min=|OB|=|OP|-=.

(3)复数加减运算的几何意义.

跟踪训练3:已知z∈C且|z|=1,求|z2-z+1|的最值.

解:因为|z|=1,所以z·=1,

所以z2-z+1=z2-z+z=z(z+-1),

所以|z2-z+1|=|z(z+-1)|=|z|·|z+-1|=|z+-1|.

设z=x+yi(x,y∈R),那么|z+-1|=|2x-1|,

又因为|z|=1,所以x2+y2=1.

所以-1≤x≤1,所以-3≤2x-1≤1,

则0≤|2x-1|≤3.

所以|z2-z+1|的最小值为0,最大值为3.

题型四　复数的综合应用

[例4] 设存在复数z同时满足下列两个条件:

(1)复数z在复平面内的对应点位于第二象限;

(2)z·+2iz=8+ai(a∈R).

求a的取值范围.

解:设z=x+yi(x,y∈R),由(1)得x<0,y>0.

由(2)得x2+y2+2i(x+yi)=8+ai,即x2+y2-2y+2xi=8+ai,

由复数相等的充要条件,得

即

因为x2+(y-1)2=9表示以(0,1)为圆心,3为半径的圆,且x<0,

所以-3≤x<0,

所以-6≤2x<0,即-6≤a<0,

所以a的取值范围是[-6,0).

复数具有代数形式,且复数z=a+bi(a,b∈R)与复平面内的点Z(a,b)之间建立了一一对应关系,复数又是数形结合的桥梁,要注意复数与向量、方程、函数等知识的交汇.

跟踪训练4: 四边形ABCD是复平面内的平行四边形,A,B,C,D四点对应的复数分别为1+3i,2i,2+i,z.

(1)求复数z;

(2)z是关于x的方程2x2-px+q=0的一个根,求实数p,q的值.

解:(1)复平面内A,B,C对应的点坐标分别为(1,3),(0,2),(2,1),

设D的坐标为(x,y),由于=,

所以(x-1,y-3)=(2,-1),

所以x-1=2,y-3=-1,

解得x=3,y=2,故D(3,2),

则点D对应的复数z=3+2i.

(2)因为3+2i是关于x的方程2x2-px+q=0的一个根,

所以3-2i是关于x的方程2x2-px+q=0的另一个根,

则3+2i+3-2i=,(3+2i)·(3-2i)=,

即p=12,q=26.

第七章　检测试题

选题明细表

一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)

1.如果复数(b∈R)的实部与虚部相等,那么b等于(　A　)

(A)-2   (B)1    (C)2    (D)4

解析:==b-2i,所以实部为b,虚部为-2,所以b=-2.故选A.

2.设x∈R,i是虚数单位,则“x=-3”是“复数z=(x2+2x-3)+(x-1)i为纯虚数”的(　C　)

(A)充分不必要条件

(B)必要不充分条件

(C)充要条件

(D)既不充分也不必要条件

解析:复数z=(x2+2x-3)+(x-1)i为纯虚数,则x2+2x-3=0且x-1≠0,解得x=-3,故x=-3⇔复数z为纯虚数.故选C.

3.若z=,则|z|等于(　A　)

(A)      (B)    (C)    (D)

解析:z===,

所以|z|==.故选A.

4.A,B分别是复数z1,z2在复平面内对应的点,O是原点,若|z1+z2|=|z1-z2|,则△AOB一定是(　B　)

(A)等腰三角形 (B)直角三角形

(C)等边三角形 (D)等腰直角三角形

解析:根据复数加(减)法的几何意义知,以,为邻边所作的平行四边形的对角线相等,则此平行四边形为矩形,故△AOB为直角三角形.故选B.

5.已知i为虚数单位,复数z=(a∈R)是纯虚数,则|-ai|等于(　C　)

(A)       (B)4     (C)3     (D)2

解析:由z==为纯虚数,

所以解得a=-2,所以|+2i|==3.故选C.

6.△ABC的三个顶点所对应的复数分别为z1,z2,z3,复数z满足|z-z1|=|z-z2|=|z-z3|,则z对应的点是△ABC的(　A　)

(A)外心 (B)内心 (C)重心 (D)垂心

解析:设复数z与复平面内的点Z相对应,由△ABC的三个顶点所对应的复数分别为z1,z2,z3,及由|z-z1|=|z-z2|=|z-z3|可知点Z到△ABC的三个顶点的距离相等,由三角形外心的定义可知,点Z即为△ABC的外心.故选A.

7.已知复数z1=3-bi,z2=1-2i,若是实数,则实数b等于(　A　)

(A)6      (B)-6    (C)0     (D)

解析:因为===是实数,

所以6-b=0,

所以实数b的值为6.故选A.

8.计算+的值等于(　C　)

(A)0 (B)1 (C)2i (D)i

解析:原式=+=+=+i=

+i=+i=2i.故选C.

二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,选对但不全的得2分,有选错的得0分)

9.若复数z=-i,则(　AC　)

(A)|z|=2               (B)|z|=4

(C)z的共轭复数 =+i (D)z2=4-2i

解析:依题意|z|==2,故A选项正确,B选项错误.

=+i,C选项正确.

z2=(-i)2=3-2i+i2=2-2i,D选项错误.故选AC.

10.设z=(-t2+4t-5)+(t2+2t+2)i,t∈R,则以下结论正确的是(　ABC　)

(A)z对应的点在第二象限

(B)z一定不为纯虚数

(C) 对应的点在实轴的下方

(D)z可以为实数

解析:因为-t2+4t-5=-(t-2)2-1<0, t2+2t+2=(t+1)2+1>0,

所以z对应的点在第二象限.故A正确;

因为-t2+4t-5=0无解,

所以z一定不为纯虚数,故B正确;

因为z与对应的点关于实轴对称,

所以对应的点在第三象限,满足在实轴的下方,故C正确;

因为t2+2t+2=0无解,

所以z一定不是实数,故D错误.故选ABC.

11.已知i为虚数单位,在复平面内,复数z=,以下说法正确的是(　CD　)

(A)复数z的虚部是i

(B)|z|=1

(C)复数z的共轭复数是 =-i

(D)复数z的共轭复数对应的点位于第四象限

解析:z====+i,

对于A,复数z的虚部是,故A错误;

对于B,|z|==,故B错误;

对于C,复数z的共轭复数是 =-i,故C正确;

对于D,=-i,在复平面内,对应点的坐标为(,-),

复数z的共轭复数对应的点位于第四象限,故D正确.故选CD.

12.已知z1与z2是共轭虚数,以下4个命题一定正确的是(　BC　)

(A)<|z2|2 (B)z1z2=|z1z2|

(C)z1+z2∈R (D)∈R

解析:z1与z2是共轭虚数,设z1=a+bi,则z2=a-bi(a,b∈R).

=a2-b2+2abi,虚数不能比较大小,选项A不正确; z1z2=|z1z2|=a2+b2,选项B正确;z1+z2=2a∈R,选项C正确;===+

i不一定是实数,选项D不一定正确.故选BC.

三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上)

13.设复数a+bi(a,b∈R)的模为,则(a+bi)(a-bi)=　　　　. 

解析:设z=a+bi,则(a+bi)(a-bi)=z=|z|2=3.

答案:3

14.已知复数z1=cos 15°+isin 15°和复数z2=cos 45°+isin 45°,则z1·z2=　　　　. 

解析:z1·z2=(cos 15°+isin 15°)(cos 45°+isin 45°)=

(cos 15°cos 45°-sin 15°sin 45°)+(sin 15°cos 45°+

cos 15°sin 45°)i=cos 60°+isin 60°=+i.

答案:+i

15.已知a∈R,若为实数,则a=　　　　,||=　　　　. 

解析:===+i.

因为为实数,

所以=0,

所以a=-.

所以||=.

答案:-　

16.已知关于x的方程x2+(1+2i)x-(3m-1)i=0有实根,则纯虚数m的值是　　　　. 

解析:方程有实根,不妨设其一根为x0,设m=ai代入方程得

+(1+2i)x0-(3ai-1)i=0,

化简得,(2x0+1)i++x0+3a=0,

所以解得a=,

所以m=i.

答案:i

四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)

已知复数z满足(1+2i)z=4+3i,求z及.

解:因为(1+2i)z=4+3i,

所以z===2-i,

故=2+i.

所以====-i.

18.(本小题满分12分)

已知复数z=a-i(a∈R),且z(1+i)是纯虚数.

(1)求复数z及|z|;

(2)在复平面内,若复数(z-mi)2(m∈R)对应点在第二象限,求实数m的取值范围.

解:(1)因为z=a-i(a∈R),且z(1+i)是纯虚数,

所以(a-i)(1+i)=(a+1)+(a-1)i是纯虚数,

则即a=-1.

所以z=-1-i,|z|==.

(2)(z-mi)2=[-1-(m+1)i]2=1-(m+1)2+2(m+1)i,

由题意可得解得m>0.

所以实数m的取值范围是(0,+∞).

19.(本小题满分12分)

已知平行四边形ABCD中,与对应的复数分别是3+2i与1+4i,两对角线AC与BD相交于P点.

(1)求对应的复数;

(2)求对应的复数;

(3)求△APB的面积.

解:(1)由于四边形ABCD是平行四边形,

所以=+,于是=-,

而(1+4i)-(3+2i)=-2+2i,

故对应的复数是-2+2i.

(2)由于=-,

而(3+2i)-(-2+2i)=5,

故对应的复数是5.

(3)由于==-=(-,-2),==(,0),

于是·=-,

而||=,||=,

所以×cos∠APB=-,

因此cos∠APB=-,

故sin∠APB=,

故S△APB=||||sin∠APB=×××=.

故△APB的面积为.

20.(本小题满分12分)

已知复数z满足|z|=,z2的虚部为2.

(1)求复数z;

(2)设z,z2,z-z2在复平面内对应的点分别为A,B,C,求△ABC的面积.

解:(1)设z=a+bi(a,b∈R),

由已知条件得a2+b2=2,z2=a2-b2+2abi,

所以2ab=2.

所以a=b=1或a=b=-1,

即z=1+i或z=-1-i.

(2)当z=1+i时,z2=(1+i)2=2i,z-z2=1-i,所以点A(1,1),B(0,2),

C(1,-1),

所以S△ABC=|AC|·1=×2×1=1;

当z=-1-i时,z2=(-1-i)2=2i,

z-z2=-1-3i.

所以点A(-1,-1),B(0,2),C(-1,-3),

所以S△ABC=|AC|·1=×2×1=1.

故△ABC的面积为1.

21.(本小题满分12分)

设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且=-3+4i.

(1)求z2及|z2|;

(2)若z1=z2,求θ与a2的值.

解:(1)设z2=x+yi(x,y∈R),

则=(x+yi)2=x2-y2+2xyi,

因此x2-y2+2xyi=-3+4i.

所以解得或

所以z2=1+2i或z2=-1-2i.

又因为z2在复平面内对应的点在第一象限,则z2=-1-2i应舍去,

故z2=1+2i,|z2|=.

(2)由(1)知(a2-4sin2θ)+(1+2cos θ)i=1+2i,

即解得cos θ=,

因为θ∈(0,π),所以θ=,

所以a2=1+4sin2θ=1+4×=4.

综上可知,θ=,a2=4.

22.(本小题满分12分)

设z是虚数,ω=z+是实数,且-1<ω<2.

(1)求|z|的值及z的实部的取值范围.

(2)设μ=,求证:μ为纯虚数.

(1)解:因为z是虚数,

所以可设z=x+yi(x,y∈R,且y≠0),

则ω=z+=(x+yi)+=x+yi+=(x+)+(y-)i.

因为ω是实数,且y≠0,

所以y-=0,即x2+y2=1.

所以|z|=1,此时ω=2x.

又-1<ω<2,所以-1<2x<2.

所以-<x<1,

即z的实部的取值范围是(-,1).

(2)证明:μ==

=

=. 

又x2+y2=1,所以μ=-i.

因为y≠0,所以μ为纯虚数.