





高考数学(理数)二轮复习专题1 第4讲《不等式》课件 (含详解)
展开1.(2019年新课标Ⅱ)若a>b,则( )A.ln(a-b)>0 B.3a<3bC.a3-b3>0 D.|a|>|b|【答案】C
【答案】[-1,7]【解析】由7+6x-x2≥0,得x2-6x-7≤0,解得-1≤x≤7.
【答案】9【解析】作出不等式组表示的可行域如图所示.由z=3x-y,得y=3x-z,当直线y=3x-z过A(3,0)时,直线在y轴上的截距最小,z有最大值,且zmax=3×3-0=9.
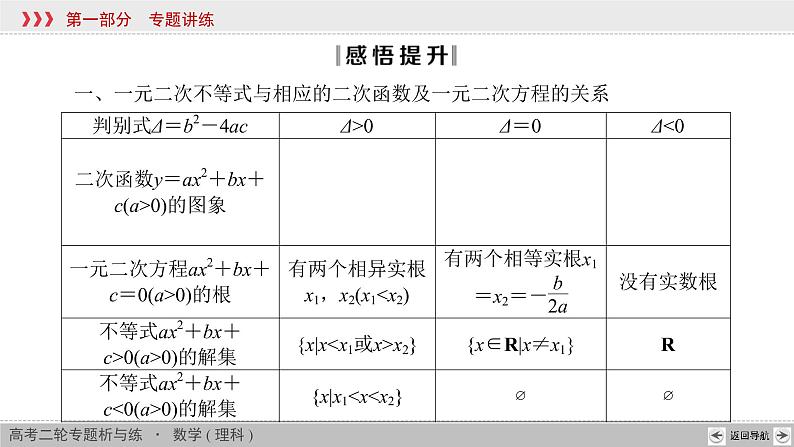
一、一元二次不等式与相应的二次函数及一元二次方程的关系
例1 (2018年新课标Ⅲ)设a=lg0.20.3,b=lg20.3,则( )A.a+b<ab<0 B.ab<a+b<0C.a+b<0<ab D.ab<0<a+b【分析】直接利用对数的运算性质变形即可比较大小.【答案】B
数、式的大小比较的常用方法:1.比较法:比较法的主要步骤为:作差——变形——因式分解(或配方)——判断正负.在所给不等式完全是积、商、幂的形式时,也可考虑作商比较.2.构造函数,利用函数单调性:观察两个比较大小的式子,分析它们的结构、字母的位置和系数是否相似(相同),然后将相同的部分不变,不同的部分看做函数f(x)的自变量,能否将两个式子转化为f(a),f(b)的形式,如果能则利用函数f(x)的单调性比较大小,不能则用其他方法比较大小.
(2019年四川攀枝花模拟)如果x+y<0且y>0,那么下列不等式成立的是( )A.y2>x2>xy B.x2>y2>-xyC.x2<-xy
例2 (2018年内蒙古呼伦贝尔模拟)关于x的不等式x2-(a+1)x+a<0的解集中,恰有3个整数,则a的取值范围是( )A.(4,5) B.(-3,-2)∪(4,5)C.(4,5] D.[-3,-2)∪(4,5]【分析】不等式等价转化为(x-1)(x-a)<0,当a>1时,得1<x<a,当a<1时,得a<x<1,由此根据解集中恰有3个整数,能求出a的取值范围.【答案】D【解析】x2-(a+1)x+a<0可化为(x-1)(x-a)<0.当a>1时,得1<x<a,此时解集中的整数为2,3,4,则4<a≤5;当a<1时,得a<x<1,则-3≤a<-2.故a的取值范围是[-3,-2)∪(4,5].故选D.
一元二次不等式的求解步骤:(1)将不等式的右边化为零,左边化为二次项系数大于零的不等式ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0).(2)求出相应的一元二次方程的根,或者判定相应的方程无根.(3)利用二次函数的图象确定一元二次不等式的解集.
(2018年山西大同期末)已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2-5x+a>0的解集是( )
【分析】先画出约束条件表示的平面区域,利用目标函数的几何意义(截距),分析后易得目标函数z=-4x+y的最大值.
【答案】C【解析】作出不等式组表示的可行域如图.由z=-4x+y,得y=4x+z.平移直线y=4x+z,当y=4x+z经过A(-1,1)时,z有最大值,最大值为-4×(-1)+1=5.故选C.
1.二元一次不等式(组)表示平面区域的判断方法(特殊点定域,等号定界):(1)若直线不过原点,特殊点常选取原点;若直线过原点,则特殊点常选取(1,0)或(0,1).(2)注意不等式中不等号有无等号,无等号时直线画成虚线,有等号时直线画成实线.(3)不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
2.求目标函数的最值的步骤:(1)在平面直角坐标系内作出可行域.(2)考虑目标函数的几何意义,将目标函数进行变形.(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解.(4)求最值:将最优解代入目标函数即可求出最大值或最小值.
【答案】-6【解析】作出不等式组表示的平面区域,可得当直线z=2x-3y过点A(0,2)时,z=2x-3y取得最小值,即zmin=2×0-3×2=-6.
【分析】由x+2y>m2+2m可得(x+2y)min>m2+2m,利用基本不等式求出x+2y的最小值再解关于m的一元二次方程即可.【答案】D
1.设全集U={1,2,3,4,5},A={x|x2-4x+3≤0,x∈N},则∁UA=( )A.{1,2,3} B.{3,4,5}C.{4,5} D.{x|x<0或x>3}【答案】C【解析】解不等式x2-4x+3≤0,得1≤x≤3,则A={x|x2-4x+3≤0,x∈N}={1,2,3},所以∁UA={4,5}.故选C.
高考数学(理数)二轮复习专题4 第2讲《统计与概率》课件 (含详解): 这是一份高考数学(理数)二轮复习专题4 第2讲《统计与概率》课件 (含详解),共60页。PPT课件主要包含了统计案例的综合应用,专题复习检测等内容,欢迎下载使用。
高考数学(理数)二轮复习专题1 第3讲《函数与方程》课件 (含详解): 这是一份高考数学(理数)二轮复习专题1 第3讲《函数与方程》课件 (含详解),共47页。PPT课件主要包含了函数图象,函数零点问题,利用导数证明不等式,专题复习检测等内容,欢迎下载使用。
高考数学(理数)二轮复习专题4 第1讲《排列、组合与二项式定理》课件 (含详解): 这是一份高考数学(理数)二轮复习专题4 第1讲《排列、组合与二项式定理》课件 (含详解),共31页。PPT课件主要包含了计数原理的应用,排列组合,二项式定理的应用,专题复习检测等内容,欢迎下载使用。












