

高中数学人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修课堂教学课件ppt
展开1.理解余弦函数的性质,会求余弦函数的周期、单调区间及最值.2.能正确使用“五点法”“图像变换法”作出余弦函数y=cs x和y=Acs(ωx+φ)的图像,能体会正弦曲线和余弦曲线的关系,并能利用余弦函数的图像和性质来解决相关的综合问题.
过山车是一项富有刺激性的娱乐项目.那种风驰电掣、有惊无险的快感令不少人着迷.过山车的运动包含了许多原理,人们在设计过山车时巧妙地运用了这些原理.一个基本的过山车构造中,包含了爬升、滑落、倒转(儿童过山车没有倒转)等几个循环路径.问题:1.函数y=cs x的图像也像过山车一样“爬升”“滑落”,这是y=cs x的什么性质?2.过山车爬升到最高点,接着滑落到最低点,然后再爬升,对应y=cs x的什么性质?y=cs x在什么位置取得最值?
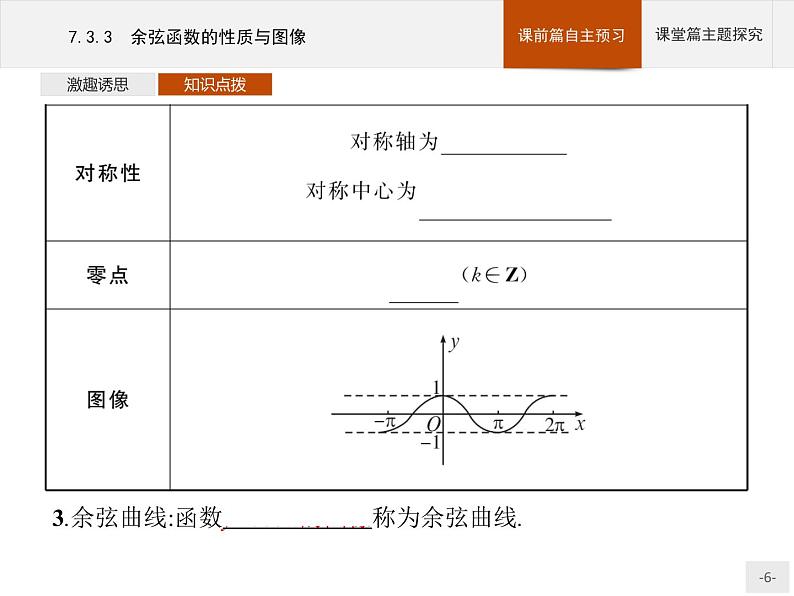
知识点一:余弦函数的性质与图像1.余弦函数:对于任意一个角x,都有唯一确定的余弦cs x与之对应,所以y=cs x是一个函数,一般称为余弦函数.2.余弦函数的性质与图像
3.余弦曲线:函数y=cs x的图像称为余弦曲线.
微练习1(多选)对于余弦函数y=cs x的图像,有以下描述,其中正确的有( )A.将[0,2π]内的图像向左、向右无限延展B.与y=sin x的图像形状完全一样,只是位置不同C.与x轴有无数个交点D.关于y轴对称
解析余弦函数y=cs x的图像,是将[0,2π]内的图像向左、向右无限“重复”得到的,不是延展,因为延展可能是拉伸,故A错误;正弦函数y=sin x的图像向左平移 个单位,会与y=cs x的图像重合,故B正确;当x=kπ+ (k∈Z)时,y=cs x=0,故余弦函数y=cs x的图像与x轴有无数个交点,故C正确;余弦函数y=cs x是偶函数,其图像关于y轴对称,故D正确.答案BCD
微练习2函数y=2cs x-1的最大值是 ,周期是 ,单调递增区间为 . 答案1 2π [2kπ-π,2kπ],k∈Z
知识点二:余弦型函数y=Acs(ωx+φ)(A>0,ω>0)的性质
分析(1)先求出函数在定义域上的单调递减区间,再验证.(2)利用诱导公式化到一个单调区间,再利用单调性比较.
答案(1)B (2)A
反思感悟 1.余弦型函数单调区间的求法(1)如果x的系数为负,则利用诱导公式变为正.(2)将ωx+φ看作整体,代入到余弦函数的单调区间解出x的范围.(3)若求具体的或一个范围内的单调区间,则给k赋值,即可求出符合条件的单调区间.2.关于三角函数值比较大小利用诱导公式,统一成正弦或余弦函数,统一化到一个单调区间内,利用单调性比较大小.
余弦函数的奇偶性、对称性
反思感悟 关于余弦型函数y=Acs(ωx+φ)的对称问题
与余弦函数有关的值域问题
反思感悟 求值域或最大值、最小值问题的一般依据及方法(1)sin x,cs x的有界性,即|sin x|≤1,|cs x|≤1;(2)sin x,cs x的单调性,通常结合函数图像来解决;(3)化为sin x=f(y)或cs x=f(y),再利用|f(y)|≤1来确定;(4)通过换元转化为二次函数问题,换元时注意变量范围的一致性.
应用数形结合法解三角不等式
方法点睛 结合函数图像解不等式,可使抽象问题直观化.
2.函数f(x)=cs(sin x)( )A.是奇函数B.是偶函数C.既是奇函数又是偶函数D.既不是奇函数也不是偶函数解析函数的定义域为R,f(-x)=cs[sin(-x)]=cs(-sin x)=cs(sin x)=f(x),所以函数f(x)=cs(sin x)是偶函数.答案B
3.(多选)已知函数f(x)=cs x,下列结论不正确的是( )A.函数y=f(x)的最小正周期为2πB.函数y=f(x)在区间(-π,0)内单调递减C.函数y=f(x)的图像关于x=π轴对称D.把函数y=f(x)的图像向左平移 个单位可得到y=sin x的图像
解析由题意,函数f(x)=cs x其最小正周期为2π,故A正确.函数在(-π,0)上单调递增,故B不正确;函数的对称轴方程是x=kπ(k∈Z),当k=1时,x=π,故C正确;把函数的图像向左平移 个单位可得
高中数学7.3.3 余弦函数的性质与图修背景图ppt课件: 这是一份高中数学7.3.3 余弦函数的性质与图修背景图ppt课件,文件包含人教B版高中数学必修三7.33余弦函数的性质与图像课件pptx、人教B版高中数学必修三7.33余弦函数的性质与图像同步练习含答案docx等2份课件配套教学资源,其中PPT共41页, 欢迎下载使用。
人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修完整版课件ppt: 这是一份人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修完整版课件ppt,共51页。PPT课件主要包含了点击右图进入等内容,欢迎下载使用。
人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修优秀ppt课件: 这是一份人教B版 (2019)必修 第三册7.3.3 余弦函数的性质与图修优秀ppt课件,共60页。PPT课件主要包含了学习目标,余弦函数的定义,余弦函数的性质,偶函数,余弦函数的图像,如图所示,常考题型,图像的变换,答案C,训练题等内容,欢迎下载使用。