专题09 几何中动角问题的两种考法-【常考压轴题】2022-2023学年七年级数学上册压轴题攻略（人教版）

这是一份专题09 几何中动角问题的两种考法-【常考压轴题】2022-2023学年七年级数学上册压轴题攻略（人教版），文件包含专题09几何中种动角问题的两种考法教师版docx、专题09几何中种动角问题的两种考法学生版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
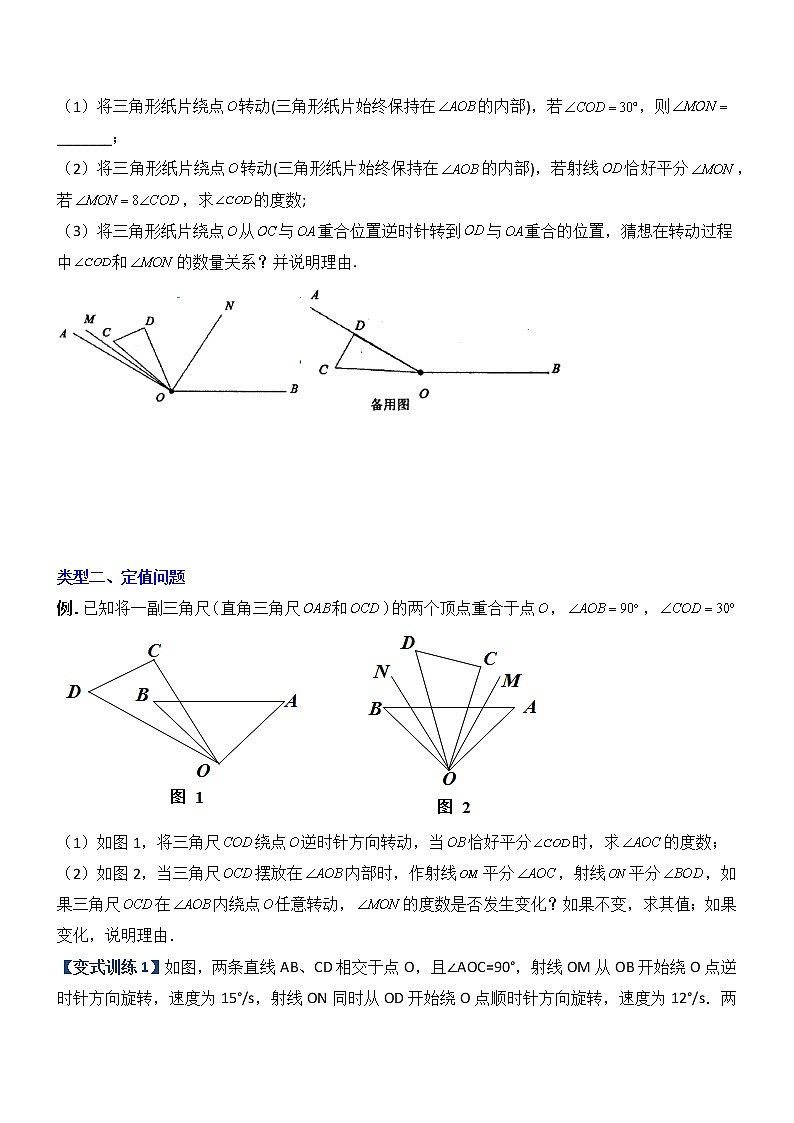
专题09 几何中动角问题的两种考法 类型一、判断角的数量之间的关系例．如图所示，O是直线上的一点，是直角，平分．（1）如图①，若，求的度数；（2）在图①，若，直接写出的度数_________（用含a的代数式表示）；（3）将图①中的绕顶点O顺时针旋转至图②的位置．①探究和的度数之间的关系，写出你的结论，并说明理由；②在的内部有一条射线，满足，试确定与的度数之间的关系，说明理由．     【变式训练1】已知∠AOB＝∠COD＝90°，OE平分∠BOC．(1)如图，若∠AOC＝30°，则∠DOE的度数是______；（直接写出答案）(2)将（1）中的条件“∠AOC＝30°”改为“∠AOC是锐角”，猜想∠DOE与∠AOC的关系，并说明理由；(3)若∠AOC是钝角，请先画出图形，再探索∠DOE与∠AOC之间的数量关系．（不用写探索过程，将结论直接写在你画的图的下面）【变式训练2】如图，以直线AB上一点O为端点作射线OC，使，将一个直角三角形的直角顶点放在点O处．（注：）（1）如图①，若直角三角板DOE的一边OD放在射线OB上，则________；（2）如图②，将直角三角板DOE转到如图位置，当OC恰好平分时，求的度数；（3）如图③，将直角三角板DOE绕点O转动，如果OD始终在的内部，直接写出和的数量关系_________．     【变式训练3】已知，，，分别平分，．(1)如图1，当，重合时，          度；(2)若将的从图1的位置绕点顺时针旋转，旋转角，满足且．①如图2，用等式表示与之间的数量关系，并说明理由；②在旋转过程中，请用等式表示与之间的数量关系，并直接写出答案．  【变式训练4】如图，已知，将一个直角三角形纸片()的一个顶点放在点处，现将三角形纸片绕点任意转动，平分斜边与的夹角，平分.（1）将三角形纸片绕点转动(三角形纸片始终保持在的内部)，若，则_______；（2）将三角形纸片绕点转动(三角形纸片始终保持在的内部)，若射线恰好平分，若，求的度数;（3）将三角形纸片绕点从与重合位置逆时针转到与重合的位置，猜想在转动过程中和的数量关系？并说明理由.     类型二、定值问题例．已知将一副三角尺（直角三角尺和）的两个顶点重合于点，，（1）如图1，将三角尺绕点逆时针方向转动，当恰好平分时，求的度数；（2）如图2，当三角尺摆放在内部时，作射线平分，射线平分，如果三角尺在内绕点任意转动，的度数是否发生变化？如果不变，求其值；如果变化，说明理由．【变式训练1】如图，两条直线AB、CD相交于点O，且∠AOC=90°，射线OM从OB开始绕O点逆时针方向旋转，速度为15°/s，射线ON同时从OD开始绕O点顺时针方向旋转，速度为12°/s．两条射线OM、ON同时运动，运动时间为t秒．（本题出现的角均小于平角）（1）当t=2时，∠MON的度数为      ，∠BON的度数为        ；∠MOC的度数为      （2）当0＜t＜12时，若∠AOM=3∠AON-60°，试求出t的值；（3）当0＜t＜6时，探究的值，问：t满足怎样的条件是定值；满足怎样的条件不是定值？   【变式训练2】已知将一副三角板（）如图1摆放，点O、A、C在一条直线上．将直角三角板绕点O逆时针方向转动，变化摆放如图位置．（1）如图1，当点O、A、C在同一条直线上时，_______度；如图2，若要恰好平分，则_______度；（2）如图3，当三角板摆放在内部时，作射线平分，射线平分，如果三角板在内绕点O任意转动，的度数是否发生变化？如果不变，求其值；如果变化，说明理由．（3）当三角板从图1的位置开始，绕点O逆时针方向旋转一周，保持射线平分、射线平分（），在旋转过程中，（2）中的结论是否保持不变？如果保持不变，请说明理由；如果变化，请说明变化的情况和结果（即旋转角度a在什么范围内时的度数是多少）．类型三、求值问题例.如图1，为直线上一点，过点作射线，，将一直角三角板（）的直角顶点放在点处，一边在射线上，另一边与都在直线的上方．（注：本题旋转角度最多．）（1）将图1中的三角板绕点以每秒的速度沿顺时针方向旋转．如图2，经过秒后，______度（用含的式子表示），若恰好平分，则______秒（直接写结果）．（2）在（1）问的基础上，若三角板在转动的同时，射线也绕点以每秒的速度沿顺时针方向旋转，如图3，经过秒后，______度（用含的式子表示）若平分，求为多少秒？（3）若（2）问的条件不变，那么经过秒平分？（直接写结果）   【变式训练1】如图，将一副直角三角尺的直角顶点C叠放在一起．（1）若∠DCE＝35°，∠ACB＝　   　；若∠ACB＝140°，则∠DCE＝　   　；（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；（3）若保持三角尺BCE不动，三角尺ACD的CD边与CB边重合，然后将三角尺ACD绕点C按逆时针方向任意转动一个角度∠BCD．设∠BCD＝α（0°＜α＜90°）①∠ACB能否是∠DCE的4倍？若能求出α的值；若不能说明理由．②三角尺ACD转动中，∠BCD每秒转动3°，当∠DCE＝21°时，转动了多少秒？【变式训练2】如图（1），∠BOC和∠AOB都是锐角，射线OB在∠AOC内部，，．（本题所涉及的角都是小于180°的角）(1)如图（2），OM平分∠BOC，ON平分∠AOC，填空：①当，时，______，______，______；②______（用含有或的代数式表示）．(2)如图（3），P为∠AOB内任意一点，直线PQ过点O，点Q在∠AOB外部：①当OM平分∠POB，ON平分∠POA，∠MON的度数为______；②当OM平分∠QOB，ON平分∠QOA，∠MON的度数为______；（∠MON的度数用含有或的代数式表示）(3)如图（4），当，时，射线OP从OC处以5°/分的速度绕点O开始逆时针旋转一周，同时射线OQ从OB处以相同的速度绕点O逆时针也旋转一周，OM平分∠POQ，ON平分∠POA，那么多少分钟时，∠MON的度数是40°？   【变式训练3】如图1，点A、O、B依次在直线上，现将射线绕点O沿顺时针方向以每秒的速度旋转，同时射线绕点O沿逆时针方向以每秒的速度旋转，如图2，设旋转时间为．（1）用含t的代数式表示：_______，_______．（2）在运动过程中，当时，求t的值．（3）在旋转过程中是否存在这样的t，使得直线平分由射线、射线、射线中的任意两条射线组成的角（大于而小于）？课后训练1．如图1，点O为直线AB上一点，过点O作射线OC，使．将一直角三角板的直角顶点放在点O处，一直角边OM在射线OB上，另一直角边ON在直线AB的下方．(1)将图1中的三角板绕点O逆时针旋转至图2，使边OM在的内部，且恰好平分．问：此时直线ON是否平分？请说明理由．(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周，在旋转过程中，第n秒时，直线ON恰好平分，则n的值为______（点接写结果）(3)若图1中的三角板绕点O旋转至图3，使ON在的内部时，的度数是多少？   2．如图所示，OA，OB，OC是以直线EF上一点O为端点的三条射线，且∠FOA＝20°，∠AOB＝60°，∠BOC＝10°，以O为端点作射线OP，OQ分别与射线OF，OC重合．射线OP从OF处开始绕点O逆时针匀速旋转，转速为1度/秒，射线OQ从OC处开始绕点O顺时针匀速旋转，（射线OQ旋转至与射线OF重合时停止，射线OP旋转至与射线OE重合时停止），两条射线同时开始旋转（旋转速度＝旋转角度÷旋转时间）．(1)直接写出射线OP停止运动时的时间．(2)当射线OP平分∠AOC时，直接写山它的旋转时间．(3)若射线OQ的转速为3度/秒，当∠POQ＝70°时，直接写出射线OP的旋转时间．(4)若∠POA＝2∠POB时，射线OQ旋转到的位置恰好将∠AOB分成度数比为1：2的两个角，直接写出射线OQ的旋转速度．3．已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC．(1)如图1，若∠AOC=48°，求∠DOE的度数；(2)如图1，若∠AOC=α，则∠DOE的度数为                (用含有α的式子表示)；(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置，试探究∠DOE和∠AOC度数之间的关系，写出你的结论，并说明理由．(4)将图1中的∠DOC绕顶点O逆时针旋转至图3的位置，其它条件不变，若∠AOC=α，则∠DOE的度数为                (用含有α的式子表示)，不必说明理由．    4．如图1，为直线上一点，过点作射线，，将一直角三角板（）的直角顶点放在点处，一边在射线上，另一边与都在直线的上方．（注：本题旋转角度最多．）（1）将图1中的三角板绕点以每秒的速度沿顺时针方向旋转．如图2，经过秒后，______度（用含的式子表示），若恰好平分，则______秒（直接写结果）．（2）在（1）问的基础上，若三角板在转动的同时，射线也绕点以每秒的速度沿顺时针方向旋转，如图3，经过秒后，______度（用含的式子表示）若平分，求为多少秒？（3）若（2）问的条件不变，那么经过秒平分？（直接写结果）  5．已知:和是直角．（1）如图，当射线在内部时，请探究和之间的关系；（2）如图2，当射线射线都在外部时，过点作射线，射线，满足，，求的度数．（3）如图3，在（2）的条件下，在平面内是否存在射线，使得，若不存在，请说明理由，若存在，求出的度数．6.已知O为直线AB上的一点，∠COE＝90°，射线OF平分∠AOE．（1）在图1中，当∠COF＝36°时，则∠BOE＝　   　，当∠COF＝m°时，则∠BOE＝　   　；以此判断∠COF和∠BOE之间的数量关系是　   　；（2）若将∠COE绕点O旋转至图2的位置，试问（1）中∠COF和∠BOE之间的数量关系是否发生变化？若不发生变化，请你加以证明；若发生变化，请你说明理由；（3）若将∠COE绕点O旋转至图3的位置，继续探究∠COF和∠BOE之间的数量关系，并说明理由．