

高考数学(理数)一轮复习学案4.2《同角三角函数的基本关系及诱导公式》(含详解)
展开4.2 同角三角函数的基本关系及诱导公式
1.同角三角函数的基本关系
(1)由三角函数的定义,同角三角函数间有以下两个等式:
①____________________;
②____________________.
(2)同角三角函数的关系式的基本用途:①根据一个角的某一三角函数值,求出该角的其他三角函数值;②化简同角的三角函数式;③证明同角的三角恒等式.
2.三角函数的诱导公式
(1)诱导公式的内容:
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
π±α
±α
2π±α
(2)诱导公式的规律:
三角函数的诱导公式可概括为:奇变偶不变,符号看象限.其中“奇变偶不变”中的奇、偶分别是指的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则正、余弦互变,正、余切互变;若是偶数倍,则函数名称________.“符号看象限”是把α当成________时,原三角函数式中的角 所在________原三角函数值的符号.注意:把α当成锐角是指α不一定是锐角,如sin(360°+ 120°)=sin120°,sin(270°+120°)=-cos120°,此时把120°当成了锐角来处理.“原三角函数”是指等号左边的函数.
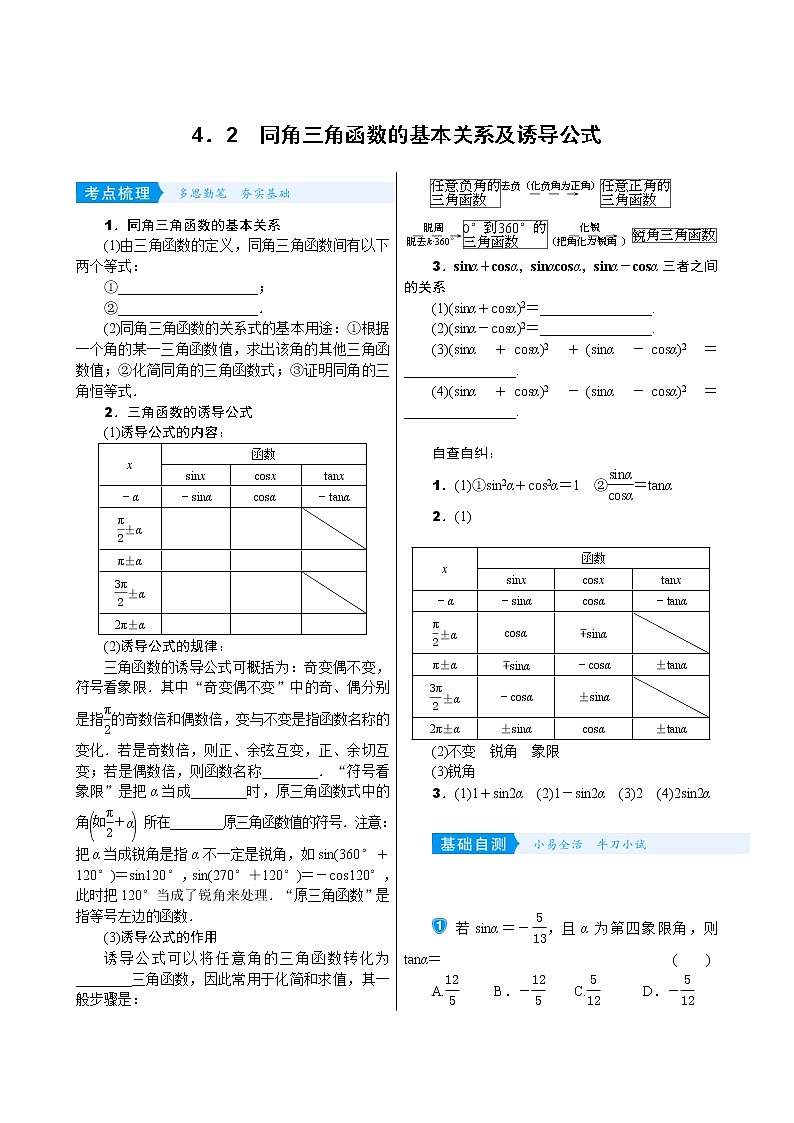
(3)诱导公式的作用
诱导公式可以将任意角的三角函数转化为________三角函数,因此常用于化简和求值,其一般步骤是:
3.sinα+cosα,sinαcosα,sinα-cosα三者之间的关系
(1)(sinα+cosα)2=________________.
(2)(sinα-cosα)2=________________.
(3)(sinα+cosα)2+(sinα-cosα)2=________________.
(4)(sinα+cosα)2-(sinα-cosα)2=________________.
自查自纠:
1.(1)①sin2α+cos2α=1 ②=tanα
2.(1)
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
cosα
∓sinα
π±α
∓sinα
-cosα
±tanα
±α
-cosα
±sinα
2π±α
±sinα
cosα
±tanα
(2)不变 锐角 象限
(3)锐角
3.(1)1+sin2α (2)1-sin2α (3)2 (4)2sin2α
若sinα=-,且α为第四象限角,则 tanα= ( )
A. B.- C. D.-
解:因为sinα=-,且α为第四象限角,所以cosα=,所以tanα=-.故选D.
()已知sinα-cosα=,则sin2α= ( )
A.- B.- C. D.
解:sin2α=2sinαcosα== -.故选A.
()= ( )
A.sin2-cos2 B.sin2+cos2
C.±(sin2-cos2) D.cos2-sin2
解:=
==|sin2-cos2|=sin2-cos2.故选A.
()若sin=-,则cos=________.
解:cos=cos=sin= -.故填-.
()已知cos=2sin,则的值为________.
解:因为cos=2sin,所以-sinα=-2cosα,则sinα=2cosα,代入sin2α+cos2α=1,得cos2α=.
所以===·cos2α-=.故填.
类型一 利用同角三角函数的基本关系式进行化简和求值
(1)()已知a∈,tanα=2,则cos=________.
解:由tanα=2得sinα=2cosα.
又sin2α+cos2α=1,所以cos2α=.
因为α∈,所以cosα=,sinα=.
因为cos=cosαcos+sinαsin,
所以cos=×+×=.
故填.
(2)()若点P(cosα,sinα)在直线y=-2x上,则cos= ( )
A.- B. C.- D.
解:由题知sinα=-2cosα,sin2α+cos2α=1,则4cos2α+cos2α=1,所以cos2α=.又cos=-sin2α=-2sinαcosα=4cos2α=.故选B.
点 拨:
给值求值的关键是找出已知式与待求式之间的联系及函数的差异.一般可以适当变换已知式,求得另外函数式的值,以备应用;另外可以变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.
(1)设sin=,且α是第二象限角,则tan的值为________.
解:因为α是第二象限角,所以是第一或第三象限角.
①当是第一象限角时,
有cos===,
所以tan==;
②当是第三象限角时,与sin=矛盾,舍去.
综上,tan=.故填.
(2)已知sinα-cosα=,α∈(0,π),则tanα=________.
解法一:由 得2cos2α+2cosα+1=0,即(cosα+1)2=0,所以cosα=-.又α∈(0,π),所以α=,tanα=tan=-1.
解法二:因为sinα-cosα=,所以(sinα-cosα)2=2,得sin2α=-1.因为α∈(0,π),所以2α∈(0,2π),2α=,所以α=,tanα=-1.故填-1.
类型二 诱导公式的应用
(1)()已知θ是第四象限角,且sin=,则tan=________.
解:由题意知,θ+是第一象限角,得cos=,
根据同角三角函数关系式可得tan=.
所以tan=tan=-=-.故填-.
(2)化简=________.
解:原式=
=-tanα.故填-tanα.
点 拨:
应用诱导公式要注意:①三角式的化简通常先用诱导公式,将角度统一后再用同角三角函数关系式,这可以避免交错使用公式时导致的混乱;②在运用公式时正确判断符号至关重要;③三角函数的化简、求值是三角函数中的基本问题,也是高考常考的问题,要予以重视;④正确理解“奇变偶不变,符号看象限”可以提高解题效率.
(1)()已知f(x)=sinx+cosx,则下列结论成立的是 ( )
A.f(x+π)=sinx+cosx B.f(π-x)=sinx+cosx
C.f=sinx+cosx D.f=sinx+cosx
解:由f(x+π)=sin(x+π)+cos(x+π)=-sinx-cosx,f(π-x)=sin(π-x)+cos(π-x)=sinx-cosx,f=sin+cos=cosx-sinx,f=sin+cos=cosx+sinx.故选D.
(2)()在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sinα=,则cos(α-β)=________.
解:因为α和β的终边关于y轴对称,所以 α+β=π+2kπ,k∈Z,那么sinβ=sinα=,cosα=-cosβ,这样cos(α-β)=cosαcosβ+sinαsinβ= -cos2α+sin2α=2sin2α-1=-.故填-.
类型三 关于sinα,cosα的齐次式问题
已知=-1,求下列各式的值.
(1);
(2)sin2α+sinαcosα+2.
解:由已知得tanα=.
(1)==-.
(2)sin2α+sinαcosα+2=+2
=+2=+2=.
点 拨:
形如asinα+bcosα和asin2α+bsinαcosα+ccos2α的式子分别称为关于sinα,cosα的一次齐次式和二次齐次式,对涉及它们的三角变换通常转化为正切(分子分母同除以cosα或cos2α)求解.如果分母为1,可考虑将1写成sin2α+cos2α.已知tanα=m的条件下,求解关于sinα,cosα的齐次式问题,必须注意以下几点:①一定是关于sinα,cosα的齐次式(或能化为齐次式)的三角函数式;②因为cosα≠0,所以可以用cosnα(n∈N*)除之,这样可以将被求式化为关于tanα的表达式,可整体代入tanα=m的值,从而完成被求式的求值运算;③注意1=sin2α+cos2α的运用.
()已知tan(5π-x)=2,则=________.
解:tan(5π-x)=2,即tan(π-x)=2,得tanx=-2.又因为2cos2-1=cosx,所以===-3.故填-3.
1.诱导公式用角度制和弧度制都可表示,运用时应注意函数名称是否要改变以及正负号的选取.
2.已知一个角的某一个三角函数值,求这个角的其他三角函数值,这类问题用同角三角函数的基本关系式求解,一般分为三种情况.
(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的,此类情况只有一组解.
(2)一个角的某一个三角函数值是已知的,但这个角所在的象限或终边所在的位置没有给出,解答这类问题,首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置,然后分不同的情况求解.
(3)一个角的某一个三角函数值是用字母给出的,此类情况须对字母进行讨论,并注意适当选取分类标准,一般有两组解.
3.计算、化简三角函数式常用技巧
(1)减少不同名的三角函数,或化切为弦,或化弦为切,如涉及sinα,cosα的齐次分式问题,常采用分子分母同除以cosnα(n∈N*),这样可以将被求式化为关于tanα的式子.
(2)巧用“1”进行变形,如1=sin2α+cos2α= tan45°等.
(3)平方关系式需开方时,应慎重考虑符号的选取.
(4)熟悉sinα+cosα,sinα-cosα,sinαcosα三者之间的内在联系,利用(sinα±cosα)2=1±2sinαcosα进行和积转换,可知一求二.
1.()已知cos=,-<θ<,则sin2θ的值等于 ( )
A.- B. C.- D.
解:由cos=,-<θ<,得sinθ=-,cosθ=,则sin2θ=2sinθcosθ=-.故选A.
2.()已知sinθ=,cosθ=,其中θ∈,则下列结论正确的是( )
A.m≤-5 B.3≤m<5
C.m=0或m=8 D.m=8
解:因为θ∈,所以sinθ=≥0 ①,cosθ=≤0 ②,且+=1,整理得=1,即5m2-22m+25=m2+10m+25,即4m(m-8)=0,解得m=0或m=8,又m=0不满足①②两式,m=8满足①②两式,故m=8.故选D.
3.()已知tanα=2,α为第一象限角,则sin2α+cosα= ( )
A. B. C. D.
解:由三角函数定义sinα=,cosα=,故sin2α+cosα=2sinαcosα+cosα=.故选C.
4.()设f(x)=asin(πx+ α)+bcos(πx+β),其中a,b,α,β都是实数,若 f(2 017)=-1,那么f(2 018)= ( )
A.1 B.2 C.0 D.-1
解:由f(2 017)=asin(2 017π+α)+bcos(2 017π+β)=-asinα-bcosβ=-1,f(2 018)=asin(2 018π+α)+bcos(2 018π+β)=asinα+bcosβ=1.故选A.
5.()若tanα=,则cos2α+2sin2α= ( )
A. B. C.1 D.
解法一:cos2α+2sin2α===.
解法二:由tanα=,得sinα=cosα,sinα=,cosα=或sinα=-,cosα=-,所以cos2α+2sin2α=+4×=.故选A.
6.()已知sinα+cosα=,α∈(0,π),则= ( )
A.- B. C. D.-
解:因为(sinα+cosα)2=1+2sinαcosα=,
所以sinαcosα=-,又α∈(0,π),所以sinα>0,cosα<0.
因为(sinα-cosα)2=1-2sinαcosα=,
所以cosα-sinα=-.
所以===-.故选A.
7.已知θ是第三象限角,且sinθ-2cosθ=-,则sinθ+cosθ=________.
解:由平方关系得+cos2θ=1,且cosθ<0,解得cosθ=-,从而sinθ=-,故sinθ+cosθ=-.故填-.
8.()已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=________.
解:y=f(x)=sin(πx+φ)-2cos(πx+φ)=sin(πx+φ-α),其中sinα=,cosα=,
因为函数的图象关于x=1对称,所以y=f(1)=±,即π+φ-α=+kπ,k∈Z,
sin2φ=sin2=sin(2α-π+2kπ)=sin(2α-π)=-sin2α=-2sinαcosα=-2××=-.故填-.
9.已知sin(3π+θ)=,求值:
+.
解:因为sin(3π+θ)=-sinθ=,所以sinθ=-.
所以原式=+
=+===
=18.
10.()已知关于x的方程2x2-(+1)x+m=0的两个根为sinθ和cosθ,θ∈(0,2π),求:
(1)+的值;
(2)m的值;
(3)方程的两根及θ的值.
解:(1)由已知得
则+=+==sinθ+cosθ=.
(2)将①式两边平方得1+2sinθcosθ=.
所以sinθcosθ=.
由②式得=,所以m=.
(3)由(2)可知原方程变为
2x2-(+1)x+=0,解得x1=,x2=.
所以或
又θ∈(0,2π),所以θ=或θ=.
11.(1)已知tanα=3,求sin2α+cos2α的值;
(2)已知=1,求的值.
解:(1)sin2α+cos2α====.
(2)由=1得tanα=2,
==
==.
()是否存在α∈,β∈(0,π),使等式sin(3π-α)= cos,cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
解:假设存在角α,β满足条件,
则由已知条件可得
由①2+②2,得sin2α+3cos2α=2.
所以sin2α=,所以sinα=±.
因为α∈,所以α=±.
当α=时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式成立;
当α=-时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式不成立,故舍去.
所以存在α=,β=满足条件.
4.2 同角三角函数的基本关系及诱导公式
1.同角三角函数的基本关系
(1)由三角函数的定义,同角三角函数间有以下两个等式:
①____________________;
②____________________.
(2)同角三角函数的关系式的基本用途:①根据一个角的某一三角函数值,求出该角的其他三角函数值;②化简同角的三角函数式;③证明同角的三角恒等式.
2.三角函数的诱导公式
(1)诱导公式的内容:
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
π±α
±α
2π±α
(2)诱导公式的规律:
三角函数的诱导公式可概括为:奇变偶不变,符号看象限.其中“奇变偶不变”中的奇、偶分别是指的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则正、余弦互变,正、余切互变;若是偶数倍,则函数名称________.“符号看象限”是把α当成________时,原三角函数式中的角 所在________原三角函数值的符号.注意:把α当成锐角是指α不一定是锐角,如sin(360°+ 120°)=sin120°,sin(270°+120°)=-cos120°,此时把120°当成了锐角来处理.“原三角函数”是指等号左边的函数.
(3)诱导公式的作用
诱导公式可以将任意角的三角函数转化为________三角函数,因此常用于化简和求值,其一般步骤是:
3.sinα+cosα,sinαcosα,sinα-cosα三者之间的关系
(1)(sinα+cosα)2=________________.
(2)(sinα-cosα)2=________________.
(3)(sinα+cosα)2+(sinα-cosα)2=________________.
(4)(sinα+cosα)2-(sinα-cosα)2=________________.
自查自纠:
1.(1)①sin2α+cos2α=1 ②=tanα
2.(1)
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
cosα
∓sinα
π±α
∓sinα
-cosα
±tanα
±α
-cosα
±sinα
2π±α
±sinα
cosα
±tanα
(2)不变 锐角 象限
(3)锐角
3.(1)1+sin2α (2)1-sin2α (3)2 (4)2sin2α
若sinα=-,且α为第四象限角,则 tanα= ( )
A. B.- C. D.-
解:因为sinα=-,且α为第四象限角,所以cosα=,所以tanα=-.故选D.
()已知sinα-cosα=,则sin2α= ( )
A.- B.- C. D.
解:sin2α=2sinαcosα== -.故选A.
()= ( )
A.sin2-cos2 B.sin2+cos2
C.±(sin2-cos2) D.cos2-sin2
解:=
==|sin2-cos2|=sin2-cos2.故选A.
()若sin=-,则cos=________.
解:cos=cos=sin= -.故填-.
()已知cos=2sin,则的值为________.
解:因为cos=2sin,所以-sinα=-2cosα,则sinα=2cosα,代入sin2α+cos2α=1,得cos2α=.
所以===·cos2α-=.故填.
类型一 利用同角三角函数的基本关系式进行化简和求值
(1)()已知a∈,tanα=2,则cos=________.
解:由tanα=2得sinα=2cosα.
又sin2α+cos2α=1,所以cos2α=.
因为α∈,所以cosα=,sinα=.
因为cos=cosαcos+sinαsin,
所以cos=×+×=.
故填.
(2)()若点P(cosα,sinα)在直线y=-2x上,则cos= ( )
A.- B. C.- D.
解:由题知sinα=-2cosα,sin2α+cos2α=1,则4cos2α+cos2α=1,所以cos2α=.又cos=-sin2α=-2sinαcosα=4cos2α=.故选B.
点 拨:
给值求值的关键是找出已知式与待求式之间的联系及函数的差异.一般可以适当变换已知式,求得另外函数式的值,以备应用;另外可以变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.
(1)设sin=,且α是第二象限角,则tan的值为________.
解:因为α是第二象限角,所以是第一或第三象限角.
①当是第一象限角时,
有cos===,
所以tan==;
②当是第三象限角时,与sin=矛盾,舍去.
综上,tan=.故填.
(2)已知sinα-cosα=,α∈(0,π),则tanα=________.
解法一:由 得2cos2α+2cosα+1=0,即(cosα+1)2=0,所以cosα=-.又α∈(0,π),所以α=,tanα=tan=-1.
解法二:因为sinα-cosα=,所以(sinα-cosα)2=2,得sin2α=-1.因为α∈(0,π),所以2α∈(0,2π),2α=,所以α=,tanα=-1.故填-1.
类型二 诱导公式的应用
(1)()已知θ是第四象限角,且sin=,则tan=________.
解:由题意知,θ+是第一象限角,得cos=,
根据同角三角函数关系式可得tan=.
所以tan=tan=-=-.故填-.
(2)化简=________.
解:原式=
=-tanα.故填-tanα.
点 拨:
应用诱导公式要注意:①三角式的化简通常先用诱导公式,将角度统一后再用同角三角函数关系式,这可以避免交错使用公式时导致的混乱;②在运用公式时正确判断符号至关重要;③三角函数的化简、求值是三角函数中的基本问题,也是高考常考的问题,要予以重视;④正确理解“奇变偶不变,符号看象限”可以提高解题效率.
(1)()已知f(x)=sinx+cosx,则下列结论成立的是 ( )
A.f(x+π)=sinx+cosx B.f(π-x)=sinx+cosx
C.f=sinx+cosx D.f=sinx+cosx
解:由f(x+π)=sin(x+π)+cos(x+π)=-sinx-cosx,f(π-x)=sin(π-x)+cos(π-x)=sinx-cosx,f=sin+cos=cosx-sinx,f=sin+cos=cosx+sinx.故选D.
(2)()在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sinα=,则cos(α-β)=________.
解:因为α和β的终边关于y轴对称,所以 α+β=π+2kπ,k∈Z,那么sinβ=sinα=,cosα=-cosβ,这样cos(α-β)=cosαcosβ+sinαsinβ= -cos2α+sin2α=2sin2α-1=-.故填-.
类型三 关于sinα,cosα的齐次式问题
已知=-1,求下列各式的值.
(1);
(2)sin2α+sinαcosα+2.
解:由已知得tanα=.
(1)==-.
(2)sin2α+sinαcosα+2=+2
=+2=+2=.
点 拨:
形如asinα+bcosα和asin2α+bsinαcosα+ccos2α的式子分别称为关于sinα,cosα的一次齐次式和二次齐次式,对涉及它们的三角变换通常转化为正切(分子分母同除以cosα或cos2α)求解.如果分母为1,可考虑将1写成sin2α+cos2α.已知tanα=m的条件下,求解关于sinα,cosα的齐次式问题,必须注意以下几点:①一定是关于sinα,cosα的齐次式(或能化为齐次式)的三角函数式;②因为cosα≠0,所以可以用cosnα(n∈N*)除之,这样可以将被求式化为关于tanα的表达式,可整体代入tanα=m的值,从而完成被求式的求值运算;③注意1=sin2α+cos2α的运用.
()已知tan(5π-x)=2,则=________.
解:tan(5π-x)=2,即tan(π-x)=2,得tanx=-2.又因为2cos2-1=cosx,所以===-3.故填-3.
1.诱导公式用角度制和弧度制都可表示,运用时应注意函数名称是否要改变以及正负号的选取.
2.已知一个角的某一个三角函数值,求这个角的其他三角函数值,这类问题用同角三角函数的基本关系式求解,一般分为三种情况.
(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的,此类情况只有一组解.
(2)一个角的某一个三角函数值是已知的,但这个角所在的象限或终边所在的位置没有给出,解答这类问题,首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置,然后分不同的情况求解.
(3)一个角的某一个三角函数值是用字母给出的,此类情况须对字母进行讨论,并注意适当选取分类标准,一般有两组解.
3.计算、化简三角函数式常用技巧
(1)减少不同名的三角函数,或化切为弦,或化弦为切,如涉及sinα,cosα的齐次分式问题,常采用分子分母同除以cosnα(n∈N*),这样可以将被求式化为关于tanα的式子.
(2)巧用“1”进行变形,如1=sin2α+cos2α= tan45°等.
(3)平方关系式需开方时,应慎重考虑符号的选取.
(4)熟悉sinα+cosα,sinα-cosα,sinαcosα三者之间的内在联系,利用(sinα±cosα)2=1±2sinαcosα进行和积转换,可知一求二.
1.()已知cos=,-<θ<,则sin2θ的值等于 ( )
A.- B. C.- D.
解:由cos=,-<θ<,得sinθ=-,cosθ=,则sin2θ=2sinθcosθ=-.故选A.
2.()已知sinθ=,cosθ=,其中θ∈,则下列结论正确的是( )
A.m≤-5 B.3≤m<5
C.m=0或m=8 D.m=8
解:因为θ∈,所以sinθ=≥0 ①,cosθ=≤0 ②,且+=1,整理得=1,即5m2-22m+25=m2+10m+25,即4m(m-8)=0,解得m=0或m=8,又m=0不满足①②两式,m=8满足①②两式,故m=8.故选D.
3.()已知tanα=2,α为第一象限角,则sin2α+cosα= ( )
A. B. C. D.
解:由三角函数定义sinα=,cosα=,故sin2α+cosα=2sinαcosα+cosα=.故选C.
4.()设f(x)=asin(πx+ α)+bcos(πx+β),其中a,b,α,β都是实数,若 f(2 017)=-1,那么f(2 018)= ( )
A.1 B.2 C.0 D.-1
解:由f(2 017)=asin(2 017π+α)+bcos(2 017π+β)=-asinα-bcosβ=-1,f(2 018)=asin(2 018π+α)+bcos(2 018π+β)=asinα+bcosβ=1.故选A.
5.()若tanα=,则cos2α+2sin2α= ( )
A. B. C.1 D.
解法一:cos2α+2sin2α===.
解法二:由tanα=,得sinα=cosα,sinα=,cosα=或sinα=-,cosα=-,所以cos2α+2sin2α=+4×=.故选A.
6.()已知sinα+cosα=,α∈(0,π),则= ( )
A.- B. C. D.-
解:因为(sinα+cosα)2=1+2sinαcosα=,
所以sinαcosα=-,又α∈(0,π),所以sinα>0,cosα<0.
因为(sinα-cosα)2=1-2sinαcosα=,
所以cosα-sinα=-.
所以===-.故选A.
7.已知θ是第三象限角,且sinθ-2cosθ=-,则sinθ+cosθ=________.
解:由平方关系得+cos2θ=1,且cosθ<0,解得cosθ=-,从而sinθ=-,故sinθ+cosθ=-.故填-.
8.()已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=________.
解:y=f(x)=sin(πx+φ)-2cos(πx+φ)=sin(πx+φ-α),其中sinα=,cosα=,
因为函数的图象关于x=1对称,所以y=f(1)=±,即π+φ-α=+kπ,k∈Z,
sin2φ=sin2=sin(2α-π+2kπ)=sin(2α-π)=-sin2α=-2sinαcosα=-2××=-.故填-.
9.已知sin(3π+θ)=,求值:
+.
解:因为sin(3π+θ)=-sinθ=,所以sinθ=-.
所以原式=+
=+===
=18.
10.()已知关于x的方程2x2-(+1)x+m=0的两个根为sinθ和cosθ,θ∈(0,2π),求:
(1)+的值;
(2)m的值;
(3)方程的两根及θ的值.
解:(1)由已知得
则+=+==sinθ+cosθ=.
(2)将①式两边平方得1+2sinθcosθ=.
所以sinθcosθ=.
由②式得=,所以m=.
(3)由(2)可知原方程变为
2x2-(+1)x+=0,解得x1=,x2=.
所以或
又θ∈(0,2π),所以θ=或θ=.
11.(1)已知tanα=3,求sin2α+cos2α的值;
(2)已知=1,求的值.
解:(1)sin2α+cos2α====.
(2)由=1得tanα=2,
==
==.
()是否存在α∈,β∈(0,π),使等式sin(3π-α)= cos,cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
解:假设存在角α,β满足条件,
则由已知条件可得
由①2+②2,得sin2α+3cos2α=2.
所以sin2α=,所以sinα=±.
因为α∈,所以α=±.
当α=时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式成立;
当α=-时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式不成立,故舍去.
所以存在α=,β=满足条件.
4.2 同角三角函数的基本关系及诱导公式
1.同角三角函数的基本关系
(1)由三角函数的定义,同角三角函数间有以下两个等式:
①____________________;
②____________________.
(2)同角三角函数的关系式的基本用途:①根据一个角的某一三角函数值,求出该角的其他三角函数值;②化简同角的三角函数式;③证明同角的三角恒等式.
2.三角函数的诱导公式
(1)诱导公式的内容:
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
π±α
±α
2π±α
(2)诱导公式的规律:
三角函数的诱导公式可概括为:奇变偶不变,符号看象限.其中“奇变偶不变”中的奇、偶分别是指的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则正、余弦互变,正、余切互变;若是偶数倍,则函数名称________.“符号看象限”是把α当成________时,原三角函数式中的角 所在________原三角函数值的符号.注意:把α当成锐角是指α不一定是锐角,如sin(360°+ 120°)=sin120°,sin(270°+120°)=-cos120°,此时把120°当成了锐角来处理.“原三角函数”是指等号左边的函数.
(3)诱导公式的作用
诱导公式可以将任意角的三角函数转化为________三角函数,因此常用于化简和求值,其一般步骤是:
3.sinα+cosα,sinαcosα,sinα-cosα三者之间的关系
(1)(sinα+cosα)2=________________.
(2)(sinα-cosα)2=________________.
(3)(sinα+cosα)2+(sinα-cosα)2=________________.
(4)(sinα+cosα)2-(sinα-cosα)2=________________.
自查自纠:
1.(1)①sin2α+cos2α=1 ②=tanα
2.(1)
x
函数
sinx
cosx
tanx
-α
-sinα
cosα
-tanα
±α
cosα
∓sinα
π±α
∓sinα
-cosα
±tanα
±α
-cosα
±sinα
2π±α
±sinα
cosα
±tanα
(2)不变 锐角 象限
(3)锐角
3.(1)1+sin2α (2)1-sin2α (3)2 (4)2sin2α
若sinα=-,且α为第四象限角,则 tanα= ( )
A. B.- C. D.-
解:因为sinα=-,且α为第四象限角,所以cosα=,所以tanα=-.故选D.
()已知sinα-cosα=,则sin2α= ( )
A.- B.- C. D.
解:sin2α=2sinαcosα== -.故选A.
()= ( )
A.sin2-cos2 B.sin2+cos2
C.±(sin2-cos2) D.cos2-sin2
解:=
==|sin2-cos2|=sin2-cos2.故选A.
()若sin=-,则cos=________.
解:cos=cos=sin= -.故填-.
()已知cos=2sin,则的值为________.
解:因为cos=2sin,所以-sinα=-2cosα,则sinα=2cosα,代入sin2α+cos2α=1,得cos2α=.
所以===·cos2α-=.故填.
类型一 利用同角三角函数的基本关系式进行化简和求值
(1)()已知a∈,tanα=2,则cos=________.
解:由tanα=2得sinα=2cosα.
又sin2α+cos2α=1,所以cos2α=.
因为α∈,所以cosα=,sinα=.
因为cos=cosαcos+sinαsin,
所以cos=×+×=.
故填.
(2)()若点P(cosα,sinα)在直线y=-2x上,则cos= ( )
A.- B. C.- D.
解:由题知sinα=-2cosα,sin2α+cos2α=1,则4cos2α+cos2α=1,所以cos2α=.又cos=-sin2α=-2sinαcosα=4cos2α=.故选B.
点 拨:
给值求值的关键是找出已知式与待求式之间的联系及函数的差异.一般可以适当变换已知式,求得另外函数式的值,以备应用;另外可以变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.
(1)设sin=,且α是第二象限角,则tan的值为________.
解:因为α是第二象限角,所以是第一或第三象限角.
①当是第一象限角时,
有cos===,
所以tan==;
②当是第三象限角时,与sin=矛盾,舍去.
综上,tan=.故填.
(2)已知sinα-cosα=,α∈(0,π),则tanα=________.
解法一:由 得2cos2α+2cosα+1=0,即(cosα+1)2=0,所以cosα=-.又α∈(0,π),所以α=,tanα=tan=-1.
解法二:因为sinα-cosα=,所以(sinα-cosα)2=2,得sin2α=-1.因为α∈(0,π),所以2α∈(0,2π),2α=,所以α=,tanα=-1.故填-1.
类型二 诱导公式的应用
(1)()已知θ是第四象限角,且sin=,则tan=________.
解:由题意知,θ+是第一象限角,得cos=,
根据同角三角函数关系式可得tan=.
所以tan=tan=-=-.故填-.
(2)化简=________.
解:原式=
=-tanα.故填-tanα.
点 拨:
应用诱导公式要注意:①三角式的化简通常先用诱导公式,将角度统一后再用同角三角函数关系式,这可以避免交错使用公式时导致的混乱;②在运用公式时正确判断符号至关重要;③三角函数的化简、求值是三角函数中的基本问题,也是高考常考的问题,要予以重视;④正确理解“奇变偶不变,符号看象限”可以提高解题效率.
(1)()已知f(x)=sinx+cosx,则下列结论成立的是 ( )
A.f(x+π)=sinx+cosx B.f(π-x)=sinx+cosx
C.f=sinx+cosx D.f=sinx+cosx
解:由f(x+π)=sin(x+π)+cos(x+π)=-sinx-cosx,f(π-x)=sin(π-x)+cos(π-x)=sinx-cosx,f=sin+cos=cosx-sinx,f=sin+cos=cosx+sinx.故选D.
(2)()在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sinα=,则cos(α-β)=________.
解:因为α和β的终边关于y轴对称,所以 α+β=π+2kπ,k∈Z,那么sinβ=sinα=,cosα=-cosβ,这样cos(α-β)=cosαcosβ+sinαsinβ= -cos2α+sin2α=2sin2α-1=-.故填-.
类型三 关于sinα,cosα的齐次式问题
已知=-1,求下列各式的值.
(1);
(2)sin2α+sinαcosα+2.
解:由已知得tanα=.
(1)==-.
(2)sin2α+sinαcosα+2=+2
=+2=+2=.
点 拨:
形如asinα+bcosα和asin2α+bsinαcosα+ccos2α的式子分别称为关于sinα,cosα的一次齐次式和二次齐次式,对涉及它们的三角变换通常转化为正切(分子分母同除以cosα或cos2α)求解.如果分母为1,可考虑将1写成sin2α+cos2α.已知tanα=m的条件下,求解关于sinα,cosα的齐次式问题,必须注意以下几点:①一定是关于sinα,cosα的齐次式(或能化为齐次式)的三角函数式;②因为cosα≠0,所以可以用cosnα(n∈N*)除之,这样可以将被求式化为关于tanα的表达式,可整体代入tanα=m的值,从而完成被求式的求值运算;③注意1=sin2α+cos2α的运用.
()已知tan(5π-x)=2,则=________.
解:tan(5π-x)=2,即tan(π-x)=2,得tanx=-2.又因为2cos2-1=cosx,所以===-3.故填-3.
1.诱导公式用角度制和弧度制都可表示,运用时应注意函数名称是否要改变以及正负号的选取.
2.已知一个角的某一个三角函数值,求这个角的其他三角函数值,这类问题用同角三角函数的基本关系式求解,一般分为三种情况.
(1)一个角的某一个三角函数值和这个角所在的象限或终边所在的位置都是已知的,此类情况只有一组解.
(2)一个角的某一个三角函数值是已知的,但这个角所在的象限或终边所在的位置没有给出,解答这类问题,首先要根据已知的三角函数值确定这个角所在的象限或终边所在的位置,然后分不同的情况求解.
(3)一个角的某一个三角函数值是用字母给出的,此类情况须对字母进行讨论,并注意适当选取分类标准,一般有两组解.
3.计算、化简三角函数式常用技巧
(1)减少不同名的三角函数,或化切为弦,或化弦为切,如涉及sinα,cosα的齐次分式问题,常采用分子分母同除以cosnα(n∈N*),这样可以将被求式化为关于tanα的式子.
(2)巧用“1”进行变形,如1=sin2α+cos2α= tan45°等.
(3)平方关系式需开方时,应慎重考虑符号的选取.
(4)熟悉sinα+cosα,sinα-cosα,sinαcosα三者之间的内在联系,利用(sinα±cosα)2=1±2sinαcosα进行和积转换,可知一求二.
1.()已知cos=,-<θ<,则sin2θ的值等于 ( )
A.- B. C.- D.
解:由cos=,-<θ<,得sinθ=-,cosθ=,则sin2θ=2sinθcosθ=-.故选A.
2.()已知sinθ=,cosθ=,其中θ∈,则下列结论正确的是( )
A.m≤-5 B.3≤m<5
C.m=0或m=8 D.m=8
解:因为θ∈,所以sinθ=≥0 ①,cosθ=≤0 ②,且+=1,整理得=1,即5m2-22m+25=m2+10m+25,即4m(m-8)=0,解得m=0或m=8,又m=0不满足①②两式,m=8满足①②两式,故m=8.故选D.
3.()已知tanα=2,α为第一象限角,则sin2α+cosα= ( )
A. B. C. D.
解:由三角函数定义sinα=,cosα=,故sin2α+cosα=2sinαcosα+cosα=.故选C.
4.()设f(x)=asin(πx+ α)+bcos(πx+β),其中a,b,α,β都是实数,若 f(2 017)=-1,那么f(2 018)= ( )
A.1 B.2 C.0 D.-1
解:由f(2 017)=asin(2 017π+α)+bcos(2 017π+β)=-asinα-bcosβ=-1,f(2 018)=asin(2 018π+α)+bcos(2 018π+β)=asinα+bcosβ=1.故选A.
5.()若tanα=,则cos2α+2sin2α= ( )
A. B. C.1 D.
解法一:cos2α+2sin2α===.
解法二:由tanα=,得sinα=cosα,sinα=,cosα=或sinα=-,cosα=-,所以cos2α+2sin2α=+4×=.故选A.
6.()已知sinα+cosα=,α∈(0,π),则= ( )
A.- B. C. D.-
解:因为(sinα+cosα)2=1+2sinαcosα=,
所以sinαcosα=-,又α∈(0,π),所以sinα>0,cosα<0.
因为(sinα-cosα)2=1-2sinαcosα=,
所以cosα-sinα=-.
所以===-.故选A.
7.已知θ是第三象限角,且sinθ-2cosθ=-,则sinθ+cosθ=________.
解:由平方关系得+cos2θ=1,且cosθ<0,解得cosθ=-,从而sinθ=-,故sinθ+cosθ=-.故填-.
8.()已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=________.
解:y=f(x)=sin(πx+φ)-2cos(πx+φ)=sin(πx+φ-α),其中sinα=,cosα=,
因为函数的图象关于x=1对称,所以y=f(1)=±,即π+φ-α=+kπ,k∈Z,
sin2φ=sin2=sin(2α-π+2kπ)=sin(2α-π)=-sin2α=-2sinαcosα=-2××=-.故填-.
9.已知sin(3π+θ)=,求值:
+.
解:因为sin(3π+θ)=-sinθ=,所以sinθ=-.
所以原式=+
=+===
=18.
10.()已知关于x的方程2x2-(+1)x+m=0的两个根为sinθ和cosθ,θ∈(0,2π),求:
(1)+的值;
(2)m的值;
(3)方程的两根及θ的值.
解:(1)由已知得
则+=+==sinθ+cosθ=.
(2)将①式两边平方得1+2sinθcosθ=.
所以sinθcosθ=.
由②式得=,所以m=.
(3)由(2)可知原方程变为
2x2-(+1)x+=0,解得x1=,x2=.
所以或
又θ∈(0,2π),所以θ=或θ=.
11.(1)已知tanα=3,求sin2α+cos2α的值;
(2)已知=1,求的值.
解:(1)sin2α+cos2α====.
(2)由=1得tanα=2,
==
==.
()是否存在α∈,β∈(0,π),使等式sin(3π-α)= cos,cos(-α)=-cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.
解:假设存在角α,β满足条件,
则由已知条件可得
由①2+②2,得sin2α+3cos2α=2.
所以sin2α=,所以sinα=±.
因为α∈,所以α=±.
当α=时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式成立;
当α=-时,由②式知cosβ=,
又β∈(0,π),所以β=,此时①式不成立,故舍去.
所以存在α=,β=满足条件.
高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案: 这是一份高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案,共12页。学案主要包含了教材概念·结论·性质重现,基本技能·思想·活动经验等内容,欢迎下载使用。
(新高考)高考数学一轮考点复习4.2《同角三角函数的基本关系与诱导公式》学案 (含详解): 这是一份(新高考)高考数学一轮考点复习4.2《同角三角函数的基本关系与诱导公式》学案 (含详解),共13页。
高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案: 这是一份高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案,共9页。学案主要包含了知识重温,小题热身等内容,欢迎下载使用。












