广西崇左市3年（2020-2022）九年级数学上学期期末试题汇编 2选择题

这是一份广西崇左市3年（2020-2022）九年级数学上学期期末试题汇编 2选择题，共25页。试卷主要包含了单选题，四象限，等内容，欢迎下载使用。
广西崇左市3年（2020-2022）九年级数学上学期期末试题汇编-01 选择题
一、单选题
1．（2022·广西崇左·九年级期末）如果两个相似三形对应边之比1：9，那么它们的对应中线之比是（    ）
A．1：2 B．1：3 C．1∶9 D．1：81
2．（2022·广西崇左·九年级期末）如图，在中，，则等于（    ）

A． B． C． D．
3．（2022·广西崇左·九年级期末）如图，直线，直线、与、、分别交于点、、和点、、，若，，则的长是（    ）

A． B． C． D．
4．（2022·广西崇左·九年级期末）将函数的图象向上平移4个单位，再向右平移2个单位，可得到的抛物线的解析式为（    ）
A． B．
C． D．
5．（2022·广西崇左·九年级期末）对于二次函数 y＝﹣（x+1）2﹣3，下列结论正确的是（　　）
A．函数图象的顶点坐标是（﹣1，﹣3）
B．当 x＞﹣1时，y随x的增大而增大
C．当x＝﹣1时，y有最小值为﹣3
D．图象的对称轴是直线x＝1
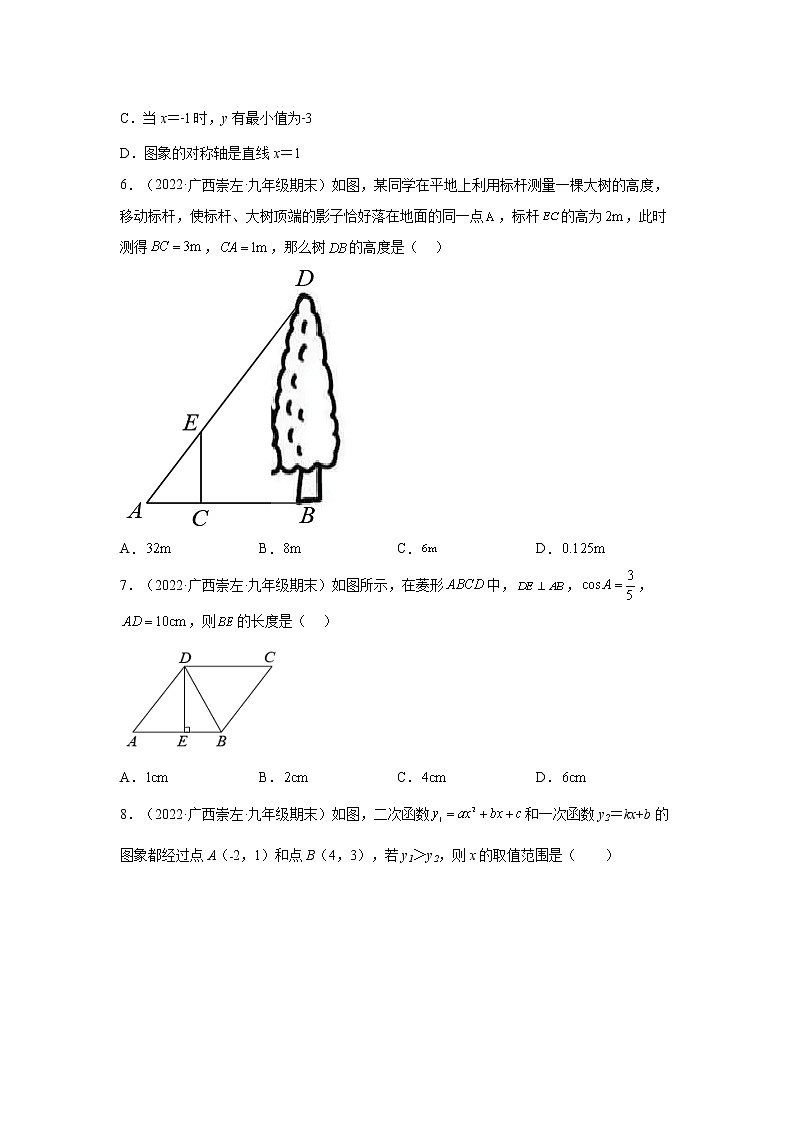
6．（2022·广西崇左·九年级期末）如图，某同学在平地上利用标杆测量一棵大树的高度，移动标杆，使标杆、大树顶端的影子恰好落在地面的同一点，标杆的高为，此时测得，，那么树的高度是（    ）

A． B． C． D．
7．（2022·广西崇左·九年级期末）如图所示，在菱形中，，，，则的长度是（    ）

A． B． C． D．
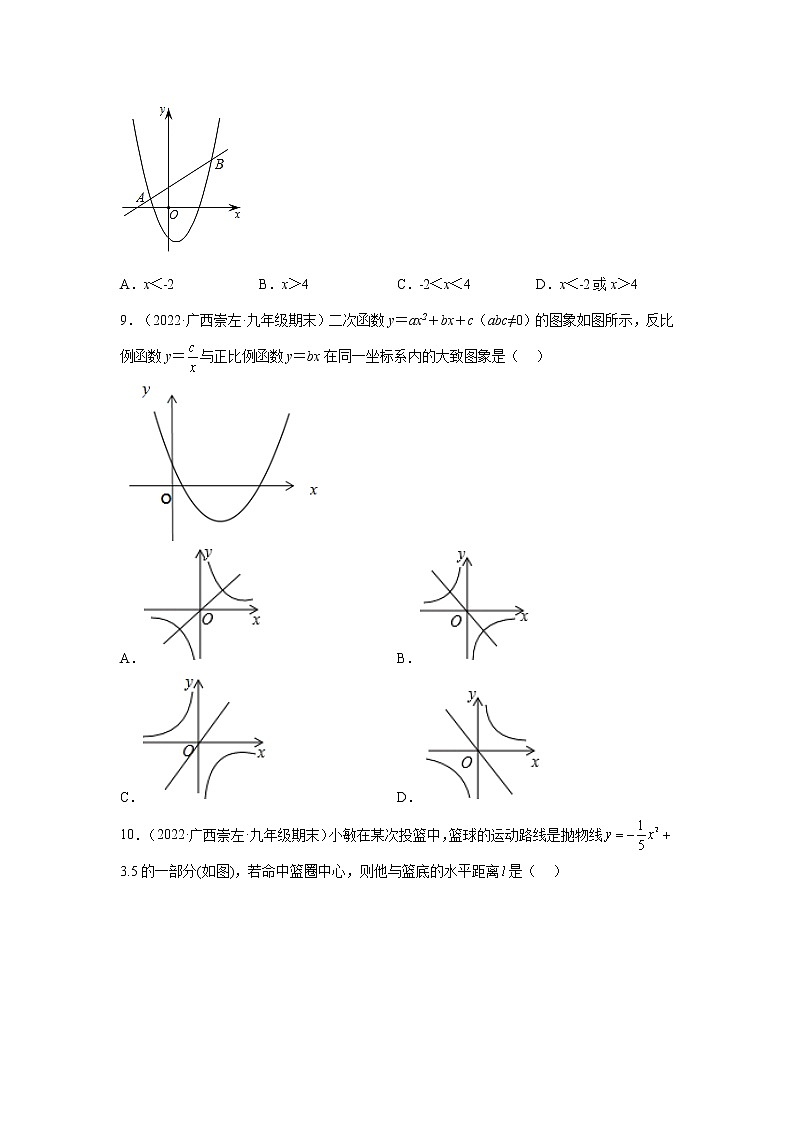
8．（2022·广西崇左·九年级期末）如图，二次函数和一次函数y2＝kx+b的图象都经过点A（﹣2，1）和点B（4，3），若y1＞y2，则x的取值范围是（　　）

A．x＜﹣2 B．x＞4 C．﹣2＜x＜4 D．x＜﹣2或x＞4
9．（2022·广西崇左·九年级期末）二次函数y＝ax2＋bx＋c（abc≠0）的图象如图所示，反比例函数y＝与正比例函数y＝bx在同一坐标系内的大致图象是（    ）

A． B．
C． D．
10．（2022·广西崇左·九年级期末）小敏在某次投篮中，篮球的运动路线是抛物线3.5的一部分(如图)，若命中篮圈中心，则他与篮底的水平距离是（    ）

A．3.5m B．3.8m C．4m D．4.5m
11．（2022·广西崇左·九年级期末）如图，在中，，点是边上一点，且，下列说法错误的是（    ）

A． B．
C． D．
12．（2022·广西崇左·九年级期末）如图，已知第一象限内的点A在反比例函数的图象上，第二象限内的B在反比例的图象上，且，则k的值是（    ）

A． B． C． D．
13．（2021·广西崇左·九年级期末）已知是锐角，则的度数是（    ）
A．30° B．45° C．60° D．90°
14．（2021·广西崇左·九年级期末）二次函数的顶点坐标是（    ）
A． B． C． D．
15．（2021·广西崇左·九年级期末）在同一直角坐标系中，关于的图象，说法正确的是（    ）
A．开口方向相同 B．都经过原点 C．都关于y轴对称 D．互相可以通过平移得到
16．（2021·广西崇左·九年级期末）如果5x=6y，那么下列结论正确的是（　　）
A． B． C． D．
17．（2021·广西崇左·九年级期末）如图，E是平行四边形ABCD的BA边的延长线上的一点，CE交AD于点F，下列各式中，错误的是(   ).

A． B． C． D．
18．（2021·广西崇左·九年级期末）关于直角三角形，下列说法正确的是（    ）
A．所有的直角三角形一定相似
B．如果直角三角形的两边长分别是3和4，那么第三边的长一定是5
C．如果已知直角三角形两个元素（直角除外），那么这个直角三角形一定可解
D．如果已知直角三角形一锐角的三角函数值，那么这个直角三角形的三边之比一定确定
19．（2021·广西崇左·九年级期末）若是函数图像上的两点，当时，下列结论正确的是（    ）
A． B． C． D．
20．（2021·广西崇左·九年级期末）已知在中，，则下列式子中正确的是（    ）
A． B． C． D．
21．（2021·广西崇左·九年级期末）如图，在矩形中，是的中点，连接，过点E作交于点．若，则的长为（    ）

A． B． C． D．1
22．（2021·广西崇左·九年级期末）如图，在中，于点，若，则的值为（    ）

A． B． C． D．
23．（2021·广西崇左·九年级期末）如图，在ABC中，D，E分别是AB,AC上的点，且DE// BC，若AE： EC=1： 4，那么的值为（ ）

A．1∶16 B．1∶18 C．1∶20 D．1∶24
24．（2021·广西崇左·九年级期末）二次函数的图象如图所示，下列结论：①；②；③的两个根是；④其中正确的有（    ）

A．1个 B．2个 C．3个 D．4个
25．（2020·广西崇左·九年级期末）四条线段成比例,其中＝3，，，则等于(    )
A．2㎝ B．㎝ C． D．8㎝
26．（2020·广西崇左·九年级期末）在反比例函数的图象的每一条曲线上，都随的增大而减小，则的取值范围是（    ）
A． B． C． D．
27．（2020·广西崇左·九年级期末）已知抛物线，则下列说法正确的是（    ）
A．抛物线开口向下 B．抛物线的对称轴是直线
C．当时，的最大值为 D．抛物线与轴的交点为
28．（2020·广西崇左·九年级期末）抛物线可由抛物线如何平移得到的（　　）
A．先向左平移3个单位，再向下平移2个单位
B．先向左平移6个单位，再向上平移7个单位
C．先向上平移2个单位，再向左平移3个单位
D．先回右平移3个单位，再向上平移2个单位
29．（2020·广西崇左·九年级期末）在中，，，则（    ）
A．60° B．90° C．120° D．135°
30．（2020·广西崇左·九年级期末）如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（　　）

A．∠B=∠C B．∠ADC=∠AEB C．BE=CD，AB=AC D．AD：AC=AE：AB
31．（2020·广西崇左·九年级期末）如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端30米的B处，测得树顶A的仰角∠ABO为α，则树OA的高度为(        )

A．米 B．30sinα米 C．30tanα米 D．30cosα米
32．（2020·广西崇左·九年级期末）如图，在平行四边形中，为延长线上一点，且，连接 交于，则△与△的周长之比为（    ）

A．9：4 B．4：9
C．3：2 D．2：3
33．（2020·广西崇左·九年级期末）在同一直角坐标系中，函数y=kx-k与（k≠0）的图象大致是（    ）
A． B． C． D．
34．（2020·广西崇左·九年级期末）如图，△ABC的顶点都是正方形网格中的格点，则sin∠ABC等于（   ）

A． B． C． D．
35．（2020·广西崇左·九年级期末）如图，在△中，，，垂足为,若，，则的值为（    ）

A． B．
C． D．
36．（2020·广西崇左·九年级期末）已知函数y=ax2+bx+c（a≠0）的图象如图，下列5个结论，其中正确的结论有（　　）
①abc＜0
②3a+c＞0
③4a+2b+c＜0
④2a+b=0
⑤b2＞4ac

A．2 B．3 C．4 D．5
【答案】
参考答案：
1．C
【分析】利用相似三角形的相似比，对应高、中线、角平分线的比，都等于相似比来解答．
【详解】解：∵两个相似三角形对应边之比是1：9，
又∵相似三角形的对应高、中线、角平分线的比等于相似比，
∴它们的对应中线之比为1：9．
故选：C．
【点睛】本题考查了相似三角形的相似比问题，须熟练掌握：①相似三角形的对应高、角平分线、中线的比等于相似比；②相似三角形的周长比等于相似比；③相似三角形的面积比等于相似比的平方．
2．B
【分析】根据正弦等于对边比斜边列式即可得解．
【详解】解:由图可知, =
故答案选:B
【点睛】本题考查了锐角三角函数的定义，是基础题．
3．C
【分析】根据平行线分线段成比例定理得出AB：BC=DE：EF，再求出答案即可．
【详解】解：∵l1∥l2∥l3，
∴AB：BC=DE：EF，
∵AB：BC=2：3，EF=9，
∴2：3= DE：EF，
∴DE=6．
故选：C．
【点睛】本题考查了平行线分线段成比例定理，能根据平行线分线段成比例定理得出正确的比例式是解题的关键．
4．C
【分析】根据“上加下减，左加右减”的原则进行解答即可．
【详解】解：二次函数的图象向上平移4个单位，所得的函数解析式为：；再向右平移2个单位所得的函数解析式为：．
故选：C．
【点睛】本题考查了二次函数的图象与几何变换，熟知“上加下减，左加右减”的原则是解答此题的关键．
5．A
【分析】由抛物线解析式可求得顶点坐标、对称轴、最值，再结合增减性可求得答案．
【详解】解：∵y＝﹣（x+1）2﹣3，
∴抛物线开口向下，对称轴为直线x＝﹣1，顶点坐标为（﹣1，﹣3），
∴当x＝﹣1时，y有最大值为﹣3，当x＞﹣1时，y随x的增大而减小，
∴只有A正确.
故选：A．
【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y＝a（x﹣h）2+k中，对称轴为x＝h，顶点坐标为（h，k）．
6．B
【分析】由题意可知,根据相似三角形对应边的比值相等的性质即可求的高．
【详解】解：由题意可知
∴
∴在中，
∵，，
∴即
∴
故选：B．
【点睛】本题考查了相似三角形的性质应用，解题关键是相似三角形对应边的比值相等．
7．C
【分析】根据余弦的值求得，进而根据菱形的性质可得，即可求得的长．
【详解】解：∵，，


四边形是菱形
∴

故选C
【点睛】本题考查了菱形的性质与余弦，根据余弦的定义求边长比是解题的关键．
8．D
【分析】根据函数图象，写出二次函数图象在一次函数图象上方部分的x的取值范围即可．
【详解】解：由图可知，x＜﹣2或x＞4时，二次函数图象在一次函数图象上方，
所以，若y1＞y2，则x的取值范围是x＜﹣2或x＞4．
故选：D．
【点睛】本题考查二次函数图象与不等式的关系，解题关键是熟练掌握二次函数图象与一次函数的关系，二次函数与方程及不等式的关系．
9．D
【分析】先根据二次函数的图象可得的符号，再根据反比例函数的图象、正比例函数的图象特点即可得．
【详解】解：抛物线的开口向上，与轴的交点位于轴的正半轴，
，
抛物线的对称轴位于轴的右侧，
，
，
由可知，反比例函数的图象位于第一、三象限，
由可知，正比例函数的图象经过原点，且经过第二、四象限，
观察四个选项可知，只有选项D符合，
故选：D．
【点睛】本题考查了二次函数、反比例函数和正比例函数的图象，熟练掌握各函数的图象特点是解题关键．
10．C
【分析】根据题意和图像可以求得当y=3.05时对应的x的值，再加上2.5m即可得解．
【详解】如图，把y=3.05代入函数3.5，解得x=1.5或x=－1.5（舍去）
则l=2.5+1.5=4（m）
故选C．
【点睛】本题考查了投球问题，我们需要根据图象解析式，求出高度y对应的水平距离x的值，结合函数图象与函数解析式是解决本题的关键．
11．D
【分析】根据和，可证得△ABD∽△DCE，△ADE∽△ACD，再逐项判断即可求解．
【详解】解：∵，
∴∠B=∠C，
∵∠ADC=∠B+∠BAD，∠ADC=∠ADE+∠CDE，，
∴∠BAD=∠CDE，
∴△ABD∽△DCE，故C正确，不符合题意；
∴，
∴，故A正确，不符合题意；
∵，
∴∠B=∠C，
∵，
∴∠ADE=∠C，
∵∠DAE=∠CAD，
∴△ADE∽△ACD，故B正确，不符合题意；
∴，∠AED=∠ADC，
∵点是边上一点，
∴AC不一定等于CD，
∴∠ADC不一定等于∠DAC，
∴∠AED不一定等于∠DAC，
∴AD不一定等于DE，故D错误，符合题意；
故选：D．
【点睛】本题主要考查了相似三角形的判定和性质，解题的关键是熟练掌握相似三角形的判定和性质定理．
12．A
【分析】作AC⊥x轴于点C，作BD⊥x轴于点D，证明△BOD∽△OAC，根据相似三角形的面积的比等于相似比的平方，即可求得△OBD的面积，再根据反比例函数中k的几何意义求解．
【详解】解：作AC⊥x轴于点C，作BD⊥x轴于点D．

∵∠ABO=30°且OA⊥OB，
∴tan30°=，
∵∠AOB=90°，
∴∠AOC+∠BOD=90°，
又∵直角△AOC中，∠AOC+∠OAC=90°，
∴∠BOD=∠OAC，
又∵∠BDO=∠ACO=90°，
∴△BOD∽△OAC，
∴=（）2=，
∴S△ODB=3S△OAC，
又∵点A在反比例函数y=的图象上，
∴S△OAC=，
∴S△ODB=，
∴k=-9．
故选：A．
【点睛】本题考查了相似三角形的性质：相似三角形的面积比是相似比的平方，以及反比例函数的比例系数k的几何意义．
13．C
【分析】根据60°角的正弦值等于解答．
【详解】解：∵，是锐角，
∴=60°，
故选C．
【点睛】本题考查了特殊角的三角函数值，是需要熟记的知识点．
14．B
【分析】由抛物线的顶点坐标式可求得答案．
【详解】解：∵二次函数
∴顶点坐标为（-1，2），
故选：B．
【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a（x-h）2+k中，对称轴为x=h，顶点坐标为（h，k）．
15．C
【分析】根据对称轴的定义,计算判断即可.
【详解】∵的开口向上，的开口向上，的开口向下，
方向不同，
∴选项A错误；
∵经过原点，不经过原点，不经过原点，
∴选项B错误；
∵对称轴为x=，
∴的对称轴都是直线x=0即y轴，
∴选项C正确；
∵向上平移2个单位可得，但不能得到，
方向不同，
∴选项D错误；
故选C.
【点睛】本题考查了抛物线的对称轴，熟练掌握对称轴的计算方法是解题的关键.
16．A
【详解】解：由 5x=6y，可以得出：x：6=y：5，
故选A．
17．A
【分析】根据平行四边形的性质得到AB∥CD，AB=CD；AD∥BC，再根据平行线分线段成比例得到==，用AB等量代换CD，得到==；再利用AF∥BC，根据平行线分线段成比例得=，由此可判断A选项中的比例是错误的．
【详解】解：∵四边形ABCD为平行四边形，
∴AB∥CD，AB=CD；AD∥BC，
∴==，而AB=CD，
∴==；
又∵AF∥BC，
∴=．
故选A．
18．D
【分析】根据题目条件，利用举反例的方法判断即可.
【详解】∵因为等腰直角三角形和一般直角三角形是不相似的，
∴选项A错误；
若斜边长为4，则第三边长为，
∴选项B错误；
已知两个角分别为45°，45°，这个直角三角形是无法求解的，
缺少解直角三角形需要的边元素，
∴选项C错误；
∵已知直角三角形的一个锐角的三角函数值，
∴就能确定斜边与直角边的比或两直角边的比，
根据勾股定理可以确定第三边的量比，
∴直角三角形的三边之比一定确定，
故选D.
【点睛】本题考查了命题的真伪，以数学基本概念，基本性质，基本法则为基础，通过举反例的方法判断是解题的关键.
19．C
【分析】先根据反比例函数的解析式判断出函数图象所在的象限，再根据x1>x2>0，判断出两点所在的象限，根据该函数在此象限内的增减性即可得出结论.
【详解】∵反比例函数y=中，k=-5x2>0，
∴两点都在第四象限，
∵在第四象限内y的值随x的增大而增大，
∴y2