四川省凉山宁南中学2021-2022学年高二上学期第二次月考数学（理）试题

这是一份四川省凉山宁南中学2021-2022学年高二上学期第二次月考数学（理）试题，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
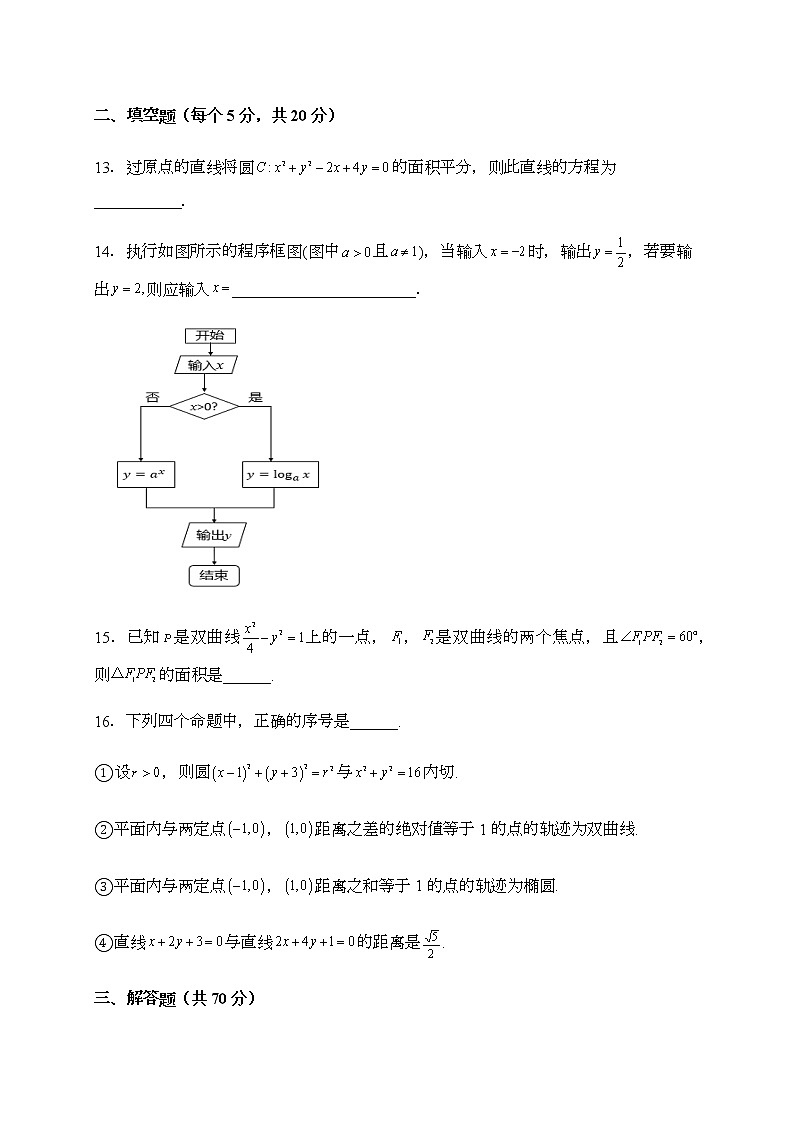
宁南中学2021—2022 学年高二上学期第二次月考试卷理科数学时间：120分钟   满分：150分一、单选题（每个5分，共60分）1．已知命题，那么是A．   B． C．D．2．椭圆x2+4y2=4的焦点坐标为（    ）A．（±2，0） B．（0，±2） C． D．3．已知椭圆上一点P到椭圆一个焦点的距离是3，则P点到另一个焦点的距离为（    ）A．5 B．3 C．2 D．74．若抛物线x2=8y上一点P到焦点的距离为8，则点P的纵坐标为（    ）A．6 B． C．7 D．5．若椭圆过点，则其焦距为（    ）A．          B．          C．           D． 6．在中，条件甲：，条件乙：，则甲是乙的（    ）.A．充分不必要条件 B．必要不充分条件C．既不充分也不必要条件 D．充要条件7．过点作圆的切线，则切线的长为（    ）A． B． C． D．8．已知三个顶点的坐标分别为，，，则外接圆的标准方程为（    ）A． B．C． D．9．“且”是“方程表示椭圆”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分又不必要条件10．下列有关命题的说法正确的是（    ）.A．命题“若，则”的否命题为：“若，则”B．“”是直线与圆相交的充要条件C．命题“若，，成等比数列，则”的逆命题为真命题D．命题“若，则”的逆否命题为真命题11．已知两点，点C是圆上任意一点，则面积的最大值是（    ）A．4 B．8 C． D．612．已知是椭圆的一个焦点，若直线与椭圆相交于两点，且，则椭圆离心率是（    ）A． B． C． D．二、填空题（每个5分，共20分）13．过原点的直线将圆的面积平分，则此直线的方程为___________.14．执行如图所示的程序框图(图中且)，当输入时，输出，若要输出则应输入_______________________．15．已知是双曲线上的一点，，是双曲线的两个焦点，且，则的面积是______.16．下列四个命题中，正确的序号是______.①设，则圆与内切.②平面内与两定点，距离之差的绝对值等于1的点的轨迹为双曲线.③平面内与两定点，距离之和等于1的点的轨迹为椭圆.④直线与直线的距离是.三、解答题（共70分）17．（10分）已知命题：关于的方程有实根；命题：关于的函数在上是增函数.（1）若是真命题，求实数的取值范围；（2）若是假命题，是真命题，求实数的取值范围. 18．（12分）已知圆C的圆心在直线上，且经过点，．Ⅰ求圆C的方程；Ⅱ已知点，，若P为圆C上的一动点，求的取值范围． 19．（12分）已知圆及直线：.(1)证明：不论取什么实数，直线与圆C总相交；(2)求直线被圆C截得的弦长的最小值及此时的直线方程. 20．（12分）已知抛物线C：y2＝2px(p＞0)过点A(2，－4)．（1）求抛物线C的方程，并求其准线方程；（2）若点B(0，2)，求过点B且与抛物线C有且仅有一个公共点的直线l的方程． 21．（12分）如图所示，四棱锥中，底面，，，，，，为的中点.（1）求证：平面；（2）求直线与平面所成角的正弦值. 22．（12分）椭圆：内有一点（1）求经过并且以为中点的弦所在直线方程；（2）如果直线：与椭圆相交于、两点，求的取值范围．2023届高二上第二次月考理科数学答案1．B  2．C  3．D   4．A  5．A    6．D.7．C  8．C  9．B   10．D  11．B   12．A13．    14．2   15．    16．②④17．（1）已知命题可化简为：或，，若是真命题，则实数的取值范围是；（2）若且是假命题，或是真命题，则满足真假和假真两种情况，则满足或，解得或，所以实数的取值范围是.18．解：Ⅰ设圆心则，即，由得，解得，，圆的半径， 圆C的方程为：．Ⅱ设，则，即则，，故的取值范围是．19．解：(1)证明：直线的方程可化为，由方程组，解得所以直线过定点M(3，1)，圆C化为标准方程为，所以圆心坐标为(1，2)，半径为5，因为定点M(3，1)到圆心(1，2)的距离为√，所以定点M(3，1)在圆内，故不论m取什么实数，过定点M(3，1)的直线与圆C总相交；(2)设直线与圆交于A、B两点，当直线与半径CM垂直与点M时，直线被截得的弦长|AB|最短，此时，此时，所以直线AB的方程为，即.20．（1）由抛物线C：过点，可得，解得.所以抛物线C的方程为，其准线方程为.（2）根据题意，易知点不在抛物线上.①当直线l的斜率不存在时，符合题意；②当直线l的斜率为0时，符合题意；③当直线l的斜率存在且不为0时，设直线l的方程为，由，得，由，得，故直线l的方程为.综上直线l的方程为或或.21．（1）证明：因为，，，所以，，在中，，，，由余弦定理可得：解得：，所以，所以是直角三角形，又为的中点，所以又，所以为等边三角形，所以，所以，又平面，平面，所以平面.（2）解：由（1）可知，以点为原点，以,，所在直线分别为轴，轴，轴建立空间直角坐标系，则，，，.所以，，.设为平面的法向量，则，即设，则，，即平面的一个法向量为，所以所以直线与平面所成角的正弦值为.22．（1）设以为中点的弦的直线与椭圆相交于,两式相减得      所求直线方程为即（2）设直线：与椭圆相交于两点，