广东省广州市荔湾区广雅中学2016-2017学年高一上学期期中数学试题 Word版含解析

这是一份广东省广州市荔湾区广雅中学2016-2017学年高一上学期期中数学试题 Word版含解析，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
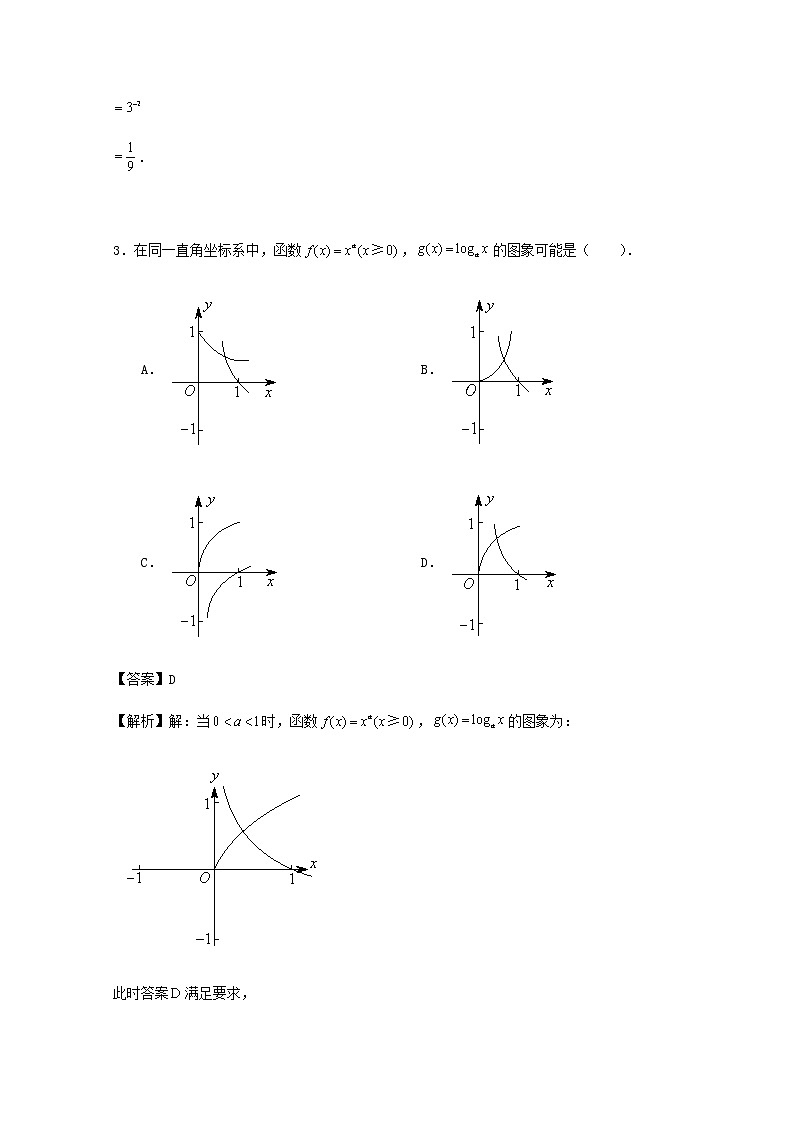
www.ks5u.com广东广雅中学2016学年度上学期期中必修一模块考试数学试卷（共4页）一、选择题：本大题共10题，每小题5分，共50分，在每小题给出的四个选项中只有一项符合题目要求。1．已知全集，集合，，则下图中的阴影部分表示的集合为（    ）．  A．    B．    C．    D．【答案】B【解析】，阴影部分表示的是，，则，故答案为． 2．已知函数，则（    ）． A．    B．    C．    D．【答案】B【解析】． 3．在同一直角坐标系中，函数，的图象可能是（    ）． A．     B．C．     D．【答案】D【解析】解：当时，函数，的图象为：此时答案满足要求，当时，函数，的图象为：无满足要求的答案，综上：故选． 4．下列函数中是偶函数且在区间上单调递增的是（    ）． A．   B．   C．   D．【答案】C【解析】对于，定义域为，非奇非偶，不满足题意；对于，定义域为，函数为奇函数，不满足题意；对于，定义域为，函数为偶函数，且在区间上单调递增，满足题意，故选；对于，定义域为，非奇非偶，不满足题意． 5．已知，则下列区间中，有实数解的是（    ）． A．   B．   C．    D．【答案】B【解析】解：∵，∴在内方程有实数解，故选：． 6．设，则，，的大小关系是（    ）． A．    B．C．    D．【答案】C【解析】因为当时，，，，所以．故本题正确答案为． 7．为了得到函数的图像，可以把函数的图像（    ）． A．向左平移个单位长度   B．向左平移个单位长度C．向右平移个单位长度   D．向右平移个单位长度【答案】D【解析】∵函数化成：，∴可以把函数的图象向右平移个单位长度得到函数的图象，故选． 8．函数的反函数记为，则的单调区间是（    ）． A．   B．   C．   D．【答案】D【解析】∵与互为反函数，∴，．则函数，，由，解得．∴函数的单调增区间是．故选：． 9．设集合，，若，则的取值范围是（    ）． A．   B．    C．    D．【答案】A【解析】根据题意，分析可得，集合是不等式的解集，由可得，，即，又由，且，则；故选． 10．设，定义符合函数则（    ）． A．   B．   C．   D．【答案】D【解析】解：对于选项，右边，而左边，显然不正确；对于选项，右边，而左边，显然不正确；对于选项，右边，而左边，显然不正确；对于选项，右边，而左边，显然正确；故选：． 二、填空题：本大题共4小题，每小题5分，共20分．11．函数的定义域是__________．【答案】【解析】解：对于函数，自变量需要满足且，即，因此，本题正确答案是． 12．已知幂函数在区间上单调递增，则实数的值为__________．【答案】【解析】由函数为幂函数，故有，又幂函数在区间单调递增，故有，所以．故本题正确答案为． 13．已知函数在上是奇函数，且当时，，则当时，的解析式为__________．【答案】【解析】本题主要考查函数的性质．依题意，在上是奇函数，且当时，，当时，，则，得，故填． 14．已知，满足对于任意实数，都有成立，则实数的取值范围为__________．【答案】【解析】解：对任意的实数，都有成立，可得函数图象上任意两点连线的斜率小于，说明函数的减函数，可得：，计算得出． 三、解答题：本大题共3小题，共30分，解答应写出文字说明，证明过程或演算步骤．15．（本小题满分分）已知函数，．（）当时，求函数的最大值与最小值．（）求实数的取值范围，使得在区间上是单调函数．【答案】见解析【解析】（）当时，，．∴时，的最小值为；时，的最大值为．（）函数的图象的对称轴为，∵在区间上是单调函数，∴或．故的取值范围是：或． 16．（本小题满分分）计算下列各式的值（）．（）．【答案】见解析【解析】（）．（）． 17．（本小题满分分）已知函数为奇函数，其中是自然对数的底数．（）求出的值．（）用定义证明在上是增函数．（）解关于的不等式．【答案】见解析【解析】（）∵为奇函数，∴，则．（）任取，，，，，即在上是增函数．（），，． 第二部分能力检测（共50分）四、填空题：本大题共3小题，每小题5分，共10分．18．某食品的保鲜时间（单位：时间）与储存温度（单位：℃）满足函数关系，（为自然对数的底数，，为常数）．若食品在℃的保险时间设计小时，在℃的保险时间是小时，该食品在℃的保鲜时间是__________小时．【答案】【解析】∵某食品的保鲜时间（单位：时间）与储存温度（单位：℃）满足函数关系（，是常数）．该食品在℃的保险时间设计小时，在℃的保险时间是小时，∴，解得，∴，∴该食品在℃的保鲜时间．故答案为：． 19．若函数有两个零点，则实数的取值范围为__________．【答案】【解析】作函数的图象如下，∵函数有两个零点，结合图象可知，． 五、解答题：本大题共3小题，共40分，解答应写出文字说明，证明过程或演算步骤．20．（本小题满分分）设是定义在上的函数，满足，当时，．（）求的值，试证明是偶函数．（）证明在上单调递减．（）若，，求的取值范围．【答案】见解析【解析】解：（）∵令得∴．令，，，，令，则．即是定义在上的偶函数．（）∵，∴，设，，，，∵，则，即，即在上单调递减．（）∵，∴，∴，∵为偶函数，且在上单调递减，∴，综上，的取值范围为． 21．（本小题满分分）已知函数．（）求函数的解析式．（）若关于的方程有两个实根，其中一个实根在区间内，另一个实根在区间内，求实数的取值范围．（）是否存在实数，使得函数的定义域为（其中）时，值域为，若存在，求出的取值范围，若不存在，说明理由．【答案】见解析【解析】（）∵，∴，则函数的解析式为．（）∵，∴，∵方程有两个实根，且，，∴．则实数的取值范围为．（），∵，∴，则在单调递增，即有两个不相同的根，且，都大于等于，，，，，且矛盾，即不存在使其成立． 22．（本小题满分分）已知二次函数（，，均为实数），满足，对于任意实数都有恒成立．（）求的值．（）求的解析式．（）当时，讨论函数在上的最大值．【答案】见解析【解析】解：（）∵，∴，即．（）∵，，∴，，∵，∴，恒成立，则，即的解析式为．（），如图所示：则，，则时，，时，，，．