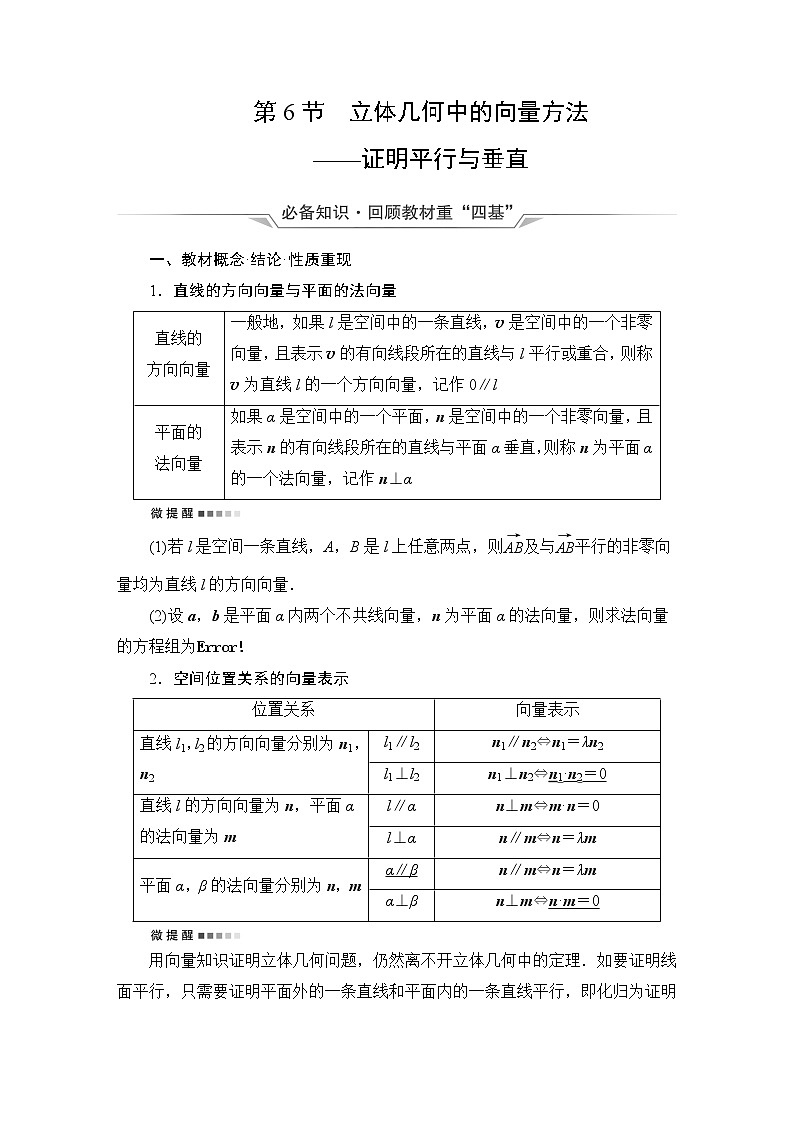
人教B版高考数学一轮总复习第7章第6节立体几何中的向量方法——证明平行与垂直学案

这是一份人教B版高考数学一轮总复习第7章第6节立体几何中的向量方法——证明平行与垂直学案，共13页。
第6节　立体几何中的向量方法——证明平行与垂直一、教材概念·结论·性质重现1．直线的方向向量与平面的法向量直线的方向向量一般地，如果l是空间中的一条直线，v是空间中的一个非零向量，且表示v的有向线段所在的直线与l平行或重合，则称v为直线l的一个方向向量，记作0∥l平面的法向量如果α是空间中的一个平面，n是空间中的一个非零向量，且表示n的有向线段所在的直线与平面α垂直，则称n为平面α的一个法向量，记作n⊥α(1)若l是空间一条直线，A，B是l上任意两点，则及与平行的非零向量均为直线l的方向向量．(2)设a，b是平面α内两个不共线向量，n为平面α的法向量，则求法向量的方程组为2．空间位置关系的向量表示位置关系向量表示直线l1，l2的方向向量分别为n1，n2l1∥l2n1∥n2⇔n1＝λn2l1⊥l2n1⊥n2⇔n1·n2＝0直线l的方向向量为n，平面α的法向量为ml∥αn⊥m⇔m·n＝0l⊥αn∥m⇔n＝λm平面α，β的法向量分别为n，mα∥βn∥m⇔n＝λmα⊥βn⊥m⇔n·m＝0用向量知识证明立体几何问题，仍然离不开立体几何中的定理．如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a∥b，只需证明向量a＝λb(λ∈R)即可．若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外．二、基本技能·思想·活动体验1．判断下列说法的正误，对的打“√”，错的打“×”．(1)直线的方向向量是唯一确定的．( × )(2)平面的单位法向量是唯一确定的．( × )(3)若两平面的法向量平行，则两平面平行．( √ )(4)若两直线的方向向量不平行，则两直线不平行．( √ )(5)若a∥b，则a所在直线与b所在直线平行．( × )(6)若空间向量a平行于平面α，则a所在直线与平面α平行．( × )2．若直线l的方向向量a＝(1，－3,5)，平面α的法向量n＝(－1,3，－5)，则有(　　)A．l∥α　　　　　　　　 B．l⊥αC．l与α斜交 D．l⊂α或l∥αB　解析：由a＝－n知，n∥a，则有l⊥α.故选B.3．平面α的一个法向量为(1,2，－2)，平面β的一个法向量为(－2，－4，k)．若α∥β，则k等于(　　)A．2　　 　 B．－4  C．4　　 　 D．－2C　解析：因为α∥β，所以两平面的法向量平行，所以＝＝，所以k＝4.4．若平面α，β垂直，则下面可以作为这两个平面的法向量的是(　　)A．n1＝(1,2,1)，n2＝(－3,1,1)B．n1＝(1,1,2)，n2＝(－2,1,1)C．n1＝(1,1,1)，n2＝(－1,2,1)D．n1＝(1,2,1)，n2＝(0，－2，－2)A　解析：两个平面垂直时其法向量也垂直，只有选项A中的两个向量垂直．5．两条不重合直线l1和l2的方向向量分别为v1＝(1,0，－1)，v2＝(－2,0,2)，则l1与l2的位置关系是________．平行　解析：因为v2＝－2v1，所以v1∥v2.又l1与l2不重合，所以l1∥l2.考点1　利用空间向量证明平行问题——基础性1．如图，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点，则平面EFG与平面PBC的位置关系是(　　)A．相交　　　　　　　　 B．平行C．垂直 D．不能确定B　解析：因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，PA⊥AD，且四边形ABCD为正方形，所以AB，AP，AD两两垂直，以A为坐标原点建立如图所示的空间直角坐标系Axyz.则A(0,0,0)，B(2,0,0)，C(2,2,0)，D(0，2,0)，P(0,0,2)，E(0,0,1)，F(0,1,1)，G(1,2,0)．因为＝(0,1,0)，＝(0,2,0)，所以＝2，所以BC∥EF.又因为EF⊄平面PBC，BC⊂平面PBC，所以EF∥平面PBC，同理可证GF∥PC，从而得出GF∥平面PBC.又EF∩GF＝F，EF⊂平面EFG，FG⊂平面EFG，所以平面EFG∥平面PBC.2．如图，在四棱锥P－ABCD中，PC⊥平面ABCD，PC＝2，在四边形ABCD中，∠ABC＝∠BCD＝90°，AB＝4，CD＝1，点M在PB上，PB＝4PM，PB与平面ABCD成30°角．求证：CM∥平面PAD.证明：由题意知，CB，CD，CP两两垂直，以C为坐标原点，CB所在直线为x轴，CD所在直线为y轴，CP所在直线为z轴建立如图所示的空间直角坐标系Cxyz.因为PC⊥平面ABCD，所以∠PBC为PB与平面ABCD所成的角，所以∠PBC＝30°.因为PC＝2，所以BC＝2，PB＝4，所以D(0,1,0)，B(2，0,0)，A(2，4,0)，P(0,0,2)，M，所以＝(0，－1,2)，＝(2，3,0)，＝.设n＝(x，y，z)为平面PAD的一个法向量，由得取y＝2，得x＝－，z＝1，所以n＝(－，2,1)是平面PAD的一个法向量．因为n·＝－×＋2×0＋1×＝0，所以n⊥.又CM⊄平面PAD，所以CM∥平面PAD.利用空间向量证明线面、面面平行的方法(1)证明线面平行的常用方法：①证明直线的方向向量与平面内的两个不共线的向量共面；②证明直线的方向向量与平面内的一个向量平行；③证明直线的方向向量与平面的法向量垂直．(2)证明面面平行常用的方法：①利用上述方法证明平面内的两个不共线向量都平行于另一个平面；②证明两个平面的法向量平行；③证明一个平面的法向量也是另一个平面的法向量．考点2　利用空间向量证明垂直问题——综合性如图，在三棱锥P－ABC中，AB＝AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．已知BC＝8，PO＝4，AO＝3，OD＝2.(1)证明：AP⊥BC；(2)若点M是线段AP上一点，且AM＝3.试证明平面AMC⊥平面BMC.证明：(1)如图所示，以O为坐标原点，分别以射线OD，OP为y轴、z轴的正半轴建立空间直角坐标系Oxyz.则O(0,0,0)，A(0，－3,0)，B(4,2,0)，C(－4，2,0)，P(0,0,4)，所以＝(0,3,4)，＝(－8,0,0)，所以·＝(0,3,4)·(－8,0,0)＝0，所以⊥，即AP⊥BC.(2)由(1)知||＝5，又||＝3，且点M在线段AP上，所以＝＝.又＝(－4，－5,0)，所以＝＋＝，则·＝(0,3,4)·＝0，所以⊥，即AP⊥BM.由(1)知AP⊥BC，且BC∩BM＝B，所以AP⊥平面BMC，于是AM⊥平面BMC.又AM⊂平面AMC，故平面AMC⊥平面BMC.利用空间向量证明线面、面面垂直的方法(1)证明线面垂直的常见思路：①将线面垂直的判定定理用向量表示；②证明直线的方向向量与平面的法向量共线．(2)证明面面垂直的常见思路：①利用面面垂直的判定定理，证明一个平面内的一条直线的方向向量为另一个平面的法向量；②证明两平面的法向量互相垂直．1．如图，在正方体ABCD－A1B1C1D1中，O是底面正方形ABCD的中心，M是D1D的中点，N是A1B1的中点，则直线ON，AM所成的角为________．90°　解析：以A为原点，分别以AB，AD，AA1所在的直线为x轴、y轴、z轴建立空间直角坐标系(图略)．设正方体的棱长为1，则A(0,0,0)，M，O，N，·O＝·＝0，所以ON与AM所成的角为90°.2．如图，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：(1)AE⊥CD；(2)PD⊥平面ABE.证明：以A为原点，AB，AD，AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系Axyz.设PA＝AB＝BC＝1，则P(0,0,1)．(1)因为∠ABC＝60°，所以△ABC为正三角形．所以C，E.设D(0，y,0)，由AC⊥CD，得·＝0，即y＝，则D，所以＝.又＝，所以·＝－×＋×＝0，所以⊥，即AE⊥CD.(2)(方法一)由(1)知，D，P(0，0,1)，所以＝.又·＝×＋×(－1)＝0，所以⊥，即PD⊥AE.因为＝(1,0,0)，所以·＝0.所以PD⊥AB.又AB∩AE＝A，AB，AE⊂平面AEB，所以PD⊥平面AEB.(方法二)由(1)知，＝(1,0,0)，＝，设平面ABE的一个法向量为n＝(x，y，z)，则令y＝2，则z＝－，所以n＝(0,2，－)为平面ABE的一个法向量．因为＝，显然＝n.因为∥n，所以⊥平面ABE，即PD⊥平面ABE.考点3　利用空间向量解决与平行、垂直有关的综合问题——应用性考向1　存在性问题如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是底面边长的倍，P为侧棱SD上的点．(1)求证：AC⊥SD；(2)若SD⊥平面PAC，侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE∶EC的值；若不存在，试说明理由．(1)证明：连接BD，设AC交BD于点O，则AC⊥BD.由题意知SO⊥平面ABCD.以O为坐标原点，OB，OC，OS所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系．设底面边长为a，则高SO＝a，所以S，D，B，C，所以＝，＝，则·＝0.故OC⊥SD.所以AC⊥SD.(2)解：棱SC上存在一点E使得BE∥平面PAC，此时SE∶EC＝2∶1.理由如下：由已知条件知是平面PAC的一个法向量，且＝，＝，＝.设＝t(0＜t≤1)，则＝＋＝＋t＝，又·＝0，所以a×＋a×＝0，所以t＝.即当SE∶EC＝2∶1时，⊥.而BE⊄平面PAC，故BE∥平面PAC.“是否存在”型问题的两种探索方式(1)根据条件做出判断，再进一步论证．(2)利用空间向量，先设出假设存在点的坐标，再根据条件求该点的坐标，即找到“存在点”，若该点坐标不能求出，或有矛盾，则判定“不存在”．考向2　折叠问题如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.(1)证明：平面PEF⊥平面ABFD；(2)求DP与平面ABFD所成角的正弦值．(1)证明：由已知可得BF⊥PF，BF⊥EF，PF∩EF＝F，PF，EF⊂平面PEF，所以BF⊥平面PEF.又BF⊂平面ABFD，所以平面PEF⊥平面ABFD.(2)解：如图，作PH⊥EF，垂足为H.由(1)得，PH⊥平面ABFD.以H为坐标原点，的方向为y轴正方向，||为单位长度，建立如图所示的空间直角坐标系Hxyz.由(1)可得，DE⊥PE.又DP＝2，DE＝1，所以PE＝.又PF＝1，EF＝2，所以EF2＝PE2＋PF2，所以PE⊥PF.所以PH＝，EH＝.则H(0,0,0)，P，D，＝，＝.又为平面ABFD的一个法向量，设DP与平面ABFD所成的角为θ，则sin θ＝|cos〈，〉|＝＝＝.所以DP与平面ABFD所成角的正弦值为.解决折叠问题的关键是弄清折叠前后的不变量．如图1，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，D，E分别是AC，AB上的点，且DE∥BC，DE＝2.将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2.(1)若M是A1D的中点，求直线CM与平面A1BE所成角的大小；(2)线段BC上是否存在点P，使平面A1DP与平面A1BE垂直？说明理由．解：(1)由折叠的性质得CD⊥DE，A1D⊥DE.又CD∩A1D＝D，所以DE⊥平面A1CD.又因为A1C⊂平面A1CD，所以A1C⊥DE.又A1C⊥CD，CD∩DE＝D，所以A1C⊥平面BCDE.建系如图，则C(0,0,0)，D(－2,0,0)，A1(0，0,2)，E(－2,2,0)，B(0,3,0)，所以＝(0,3，－2)，＝(－2,2，－2)．设平面A1BE的一个法向量为n＝(x，y，z)，则所以取z＝，则x＝－1，y＝2，所以n＝(－1,2，)为平面A1BE的一个法向量．又因为M(－1,0，)，所以＝(－1,0，)，所以cos〈，n〉＝＝＝.所以CM与平面A1BE所成角的大小为45°.(2)假设线段BC上存在点P满足条件，设P点坐标为(0，a,0)，a∈[0,3]，所以＝(0，a，－2)，＝(2，a,0)．设平面A1DP的一个法向量为n1＝(x1，y1，z1)，则取y1＝6，则x1＝－3a，z1＝a，所以n1＝(－3a,6，a)．若平面A1DP与平面A1BE垂直，则n1·n＝0，所以3a＋12＋3a＝0，即6a＝－12，所以a＝－2.因为0≤a≤3，所以a＝－2舍去．所以线段BC上不存在点P，使平面A1DP与平面A1BE垂直．