

人教B版高考数学一轮总复习第10章第1节基本计数原理、排列与组合学案
展开课程标准 | 命题解读 |
1.理解样本点、有限样本空间、随机事件. 2.会计算古典概型中简单随机事件的概率,加深对随机现象的认识和理解. 3.理解两个基本计数原理,运用计数原理探索排列、组合、二项式定理等问题. 4.了解条件概率及其与独立性的关系,能进行简单计算. 5.感悟离散型随机变量及其分布列的含义,知道可以通过随机变量更好地刻画随机现象. 6.理解伯努利试验,掌握二项分布,了解超几何分布. 7.感悟服从正态分布的随机变量,知道连续型随机变量. 8.基于随机变量及其分布解决简单的实际问题. | 考查形式:高考在本章一般命制一道选择题或填空题及一道解答题. 考查内容:两个计数原理、排列与组合、二项式定理、概率、随机变量及其分布,其中概率、随机变量及其分布是高考命题的热点,每年必考. 备考策略:(1)计数原理常与古典概型综合. (2)掌握二项式定理及其应用,会利用通项公式求特定项. (3)加强以实际问题为背景,考查分布列、期望等是高考的热点题型的训练. (4)概率统计试题的阅读量和信息量都有所加强,考查角度趋向于应用概率统计知识对实际问题做出决策. 核心素养:数学建模、数学运算、逻辑推理. |
第1节 基本计数原理、排列与组合
一、教材概念·结论·性质重现
1.两个计数原理
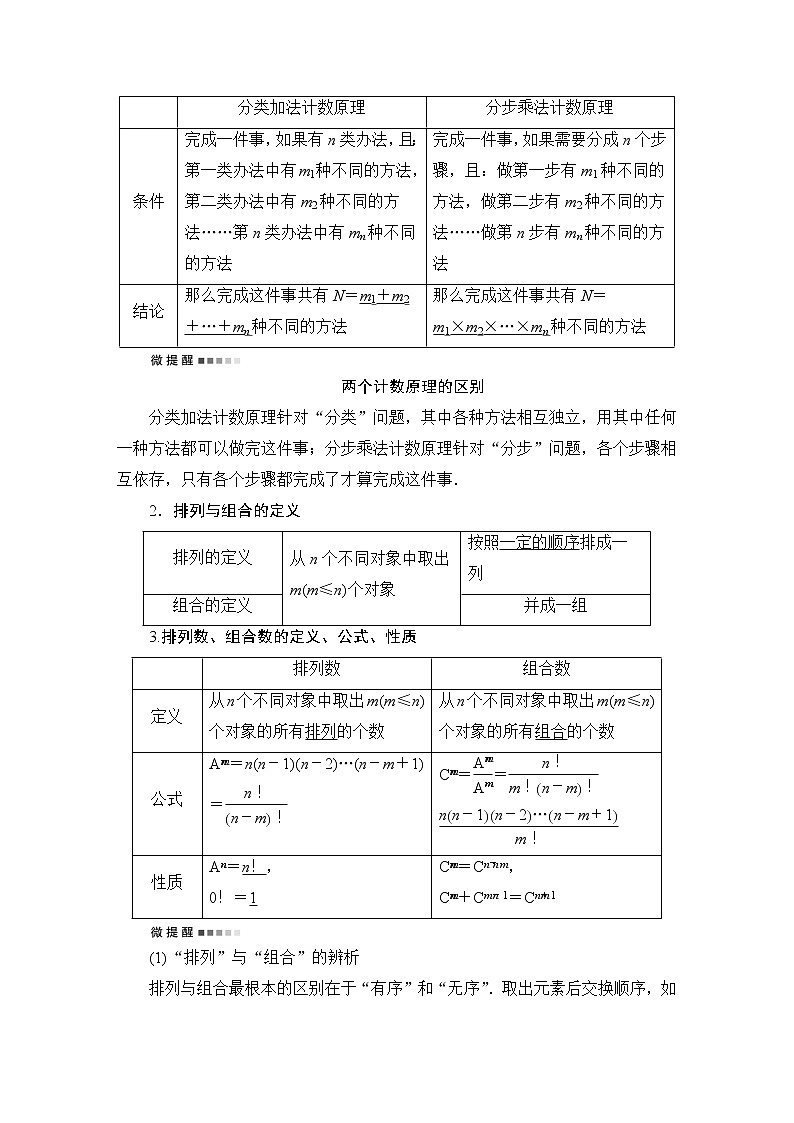
| 分类加法计数原理 | 分步乘法计数原理 |
条件 | 完成一件事,如果有n类办法,且:第一类办法中有m1种不同的方法,第二类办法中有m2种不同的方法……第n类办法中有mn种不同的方法 | 完成一件事,如果需要分成n个步骤,且:做第一步有m1种不同的方法,做第二步有m2种不同的方法……做第n步有mn种不同的方法 |
结论 | 那么完成这件事共有N=m1+m2+…+mn种不同的方法 | 那么完成这件事共有N=m1×m2×…×mn种不同的方法 |
两个计数原理的区别
分类加法计数原理针对“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对“分步”问题,各个步骤相互依存,只有各个步骤都完成了才算完成这件事.
2.排列与组合的定义
排列的定义 | 从n个不同对象中取出m(m≤n)个对象 | 按照一定的顺序排成一列 |
组合的定义 | 并成一组 |
3.排列数、组合数的定义、公式、性质
| 排列数 | 组合数 |
定义 | 从n个不同对象中取出m(m≤n)个对象的所有排列的个数 | 从n个不同对象中取出m(m≤n)个对象的所有组合的个数 |
公式 | A=n(n-1)(n-2)…(n-m+1)= | C== |
性质 | A=n!, 0!=1 | C=C, C+C=C |
(1)“排列”与“组合”的辨析
排列与组合最根本的区别在于“有序”和“无序”.取出元素后交换顺序,如果与顺序有关,则是排列;如果与顺序无关,则是组合.
(2)①排列数与组合数之间的联系:CA=A;
②两种形式:连乘积形式;阶乘形式.
前者多用于数字计算,后者多用于含有字母的排列数式子的变形与论证.
二、基本技能·思想·活动体验
1.判断下列说法的正误,对的打“√”,错的打“×”.
(1)在分类加法计数原理中,两类不同方案中的方法可以相同.( × )
(2)在分类加法计数原理中,每类方案中的方法都能直接完成这件事.( √ )
(3)所有元素完全相同的两个排列为相同排列.( × )
(4)两个组合相同的充要条件是其中的元素完全相同.( √ )
(5)若C=C,则x=m成立.( × )
2.有4位教师在同一年级的4个班中各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则不同的监考方法有( )
A.8种 B.9种
C.10种 D.11种
B 解析:设四位监考教师分别为A,B,C,D,所教班分别为a,b,c,d.假设A监考b,则余下三人监考剩下的三个班,共有3种不同方法,同理A监考c,d时,也分别有3种不同方法.由分类加法计数原理,共有3+3+3=9(种)不同的监考方法.
3.某中学语文老师从《红楼梦》《平凡的世界》《红岩》《老人与海》4本不同的名著中选出3本,分给三个同学去读,其中《红楼梦》为必读,则不同的分配方法共有( )
A.6种 B.12种
C.18种 D.24种
C 解析:(1)先从《平凡的世界》《红岩》《老人与海》三本书中选择2本,共有C=3(种)选法;(2)将选出的2本书与《红楼梦》共计3本书进行全排列,对应分给三个学生,有A=6(种)排法.根据分步乘法计数原理,不同的分配方法有3×6=18(种).故选C.
4.由数字2,0,1,9组成没有重复数字的四位偶数的个数为________.
10 解析:根据所组成的没有重复数字的四位偶数的个位是否为0进行分类计数:第一类,个位是0时,满足题意的四位偶数的个数为A=6;第二类,个位是2时,满足题意的四位偶数的个数为CA=4.由分类加法计数原理,得满足题意的四位偶数的个数为6+4=10.
5.从2名女生、4名男生中选3人参加学科竞赛,且至少有1名女生入选,则不同的选法共有________种(用数字作答).
16 解析:(方法一)可分两种情况:第一种情况,只有1名女生入选,不同的选法有CC=12(种);第二种情况,有2名女生入选,不同的选法有CC=4(种).根据分类加法计数原理知,至少有1名女生入选的不同的选法共有12+4=16(种).
(方法二)从6人中任选3人,不同的选法共有C=20(种).从6人中任选3人都是男生,不同的选法有C=4(种).所以,至少有1名女生入选的不同的选法共有20-4=16(种).
考点1 两个原理的应用——基础性
(1)用数字0,1,2,3,4组成没有重复数字且大于3 000的四位数,这样的四位数有( )
A.250个 B.249个
C.48个 D.24个
C 解析:分两类:①当千位上的数字为4时,满足条件的四位数有A=24(个);②当千位上的数字为3时,满足条件的四位数有A=24(个).由分类加法计数原理,得所有满足条件的四位数共有24+24=48(个).故选C.
(2)某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有( )
A.4种 B.10种
C.18种 D.20种
B 解析:分两种情况:①4位朋友中有2个人得到画册,有C=6(种)赠送方法;②4位朋友中只有1个人得到画册,有C=4(种)赠送方法.由分类加法计数原理,得不同的赠送方法共有6+4=10(种).故选B.
(3)(2021·青岛质检)如图,将4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的矩形不同色,则不同的涂法有( )
A.72种 B.48种
C.24种 D.12种
A 解析:(方法一)分四步完成,首先涂A有4种涂法,则涂B有3种涂法,C与A,B相邻,则C有2种涂法,D只与C相邻,则D有3种涂法.由分步乘法计数原理,得不同的涂法有4×3×2×3=72(种).
(方法二)按要求涂色至少需要3种颜色,故分两类:一是4种颜色都用,这时A有4种涂法,B有3种涂法,C有2种涂法,D有1种涂法,共有4×3×2×1=24(种)涂法;二是用3种颜色,这时A,B,C的涂法有4×3×2=24(种),D只要不与C同色即可,故D有2种涂法.所以不同的涂法共有24+24×2=72(种).
两个计数原理的应用
(1)应用两个计数原理的难点在于明确是分类还是分步:分类要做到“不重不漏”,正确把握分类标准是关键;分步要做到“步骤完整”,步步相连才能将事件完成.
(2)较复杂的问题可借助图表来完成.
(3)对于涂色问题:①分清元素的数目以及在不相邻的区域内是否可以使用同类元素;②注意对每个区域逐一进行,分步处理.
1.甲、乙、丙三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回给甲,则不同的传递方式共有( )
A.4种 B.6种
C.10种 D.16种
B 解析:分两类:甲第一次踢给乙时,满足条件的传递方式有3种(如图);同理,甲第一次踢给丙时,满足条件的传递方式也有3种.
由分类加法计数原理可知,共有3+3=6(种)传递方式.
2.如果一个三位正整数如“a1a2a3”满足a1<a2,且a2>a3,则称这样的三位数为凸数(如120,343,275等),那么所有凸数的个数为( )
A.240 B.204
C.729 D.920
A 解析:分两类:①如果这个三位数含0,则0必在末位,共有这样的凸数C个;②如果这个三位数不含0,则这样的凸数共有(CA+C)个.综上所述,所有凸数共有2C+CA=240(个).
3.如图所示的五个区域中,现有四种颜色可供选择,要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
A.24 B.48
C.72 D.96
C 解析:(方法一:以位置为主考虑)分两种情况:
(1)A,C不同色,先涂A有4种,C有3种,E有2种,B,D各有1种,有4×3×2=24(种)涂法.
(2)A,C同色,先涂A有4种,E有3种,C有1种,B,D各有2种,有4×3×2×2=48(种)涂法.
故共有24+48=72(种)涂色方法.
(方法二:以颜色为主考虑)分两类:
(1)取4色:着色方法有2A=48(种).
(2)取3色:着色方法有A=24(种).
所以共有着色方法48+24=72(种).
考点2 排列问题——基础性
(1)(2020·合肥市第二次质量检测)某部队在一次军演中要先后执行A,B,C,D,E,F六项不同的任务,要求:任务A必须排在前三项执行,且执行任务A之后需立即执行任务E,任务B,C不能相邻,则不同的执行方案共有( )
A.36种 B.44种
C.48种 D.54种
B 解析:由题意知任务A,E必须相邻,且只能安排为AE,由此分三类完成:①当AE排第一、二位置时,用○表示其他任务,则顺序为AE○○○○,余下四项任务,先全排D,F两项任务,然后将任务B,C插入D,F两项任务形成的三个空隙中,有AA种方法.②当AE排第二、三位置时,顺序为○AE○○○,余下四项任务又分为两类:①B,C两项任务中一项排第一位置,剩余三项任务排在后三个位置,有AA种方法;②D,F两项任务中一项排第一位置,剩余三项任务排在后三个位置,且任务B,C不相邻,有AA种方法.③当AE排第三、四位置时,顺序为○○AE○○,第一、二位置必须分别排来自B,C和D,F中的一个,余下两项任务排在后两个位置,有CCAA种方法.根据分类加法计数原理知不同的执行方案共有AA+AA+AA+CCAA=44(种).故选B.
(2)(2020·全国卷Ⅱ)4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有________种.
36 解析:因为4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,所以先取2名同学看作一组,选法有C=6(种).现在可看成是3组同学分配到3个小区,分法有A=6(种).根据分步乘法计数原理,可得不同的安排方法共有6×6=36(种).
1.(2020·洛阳市第一次联考)某小区有排成一排的7个车位,现有3辆不同型号的车需要停放.如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为( )
A.16 B.18
C.24 D.32
C 解析:第一步,将3辆不同型号的车进行排列,有A种方法;第二步,把剩余的4个车位看成一个元素,插入3辆车所形成的4个空位中,有C种方法.由分步乘法计数原理可知,不同的停放方法共有A·C=24(种).故选C.
2.(2020·雅礼中学高三模拟)现有10名学生排成一排,其中4名男生,6名女生.若有且只有3名男生相邻排在一起,则不同的排法共有( )
A.AA种 B.AA种
C.AAA种 D.AAA种
D 解析:采用捆绑法和插空法.从4名男生中选择3名,进而将3个相邻的男生捆在一起,看成1个男生,方法数是A,这样与第4个男生看成是2个男生;然后6个女生任意排的方法数是A;最后在6个女生形成的7个空隙中,插入2个男生,方法数是A.综上所述,不同的排法共有AAA种.故选D.
3.(2020·和平区高三一模)国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为( )
A.378 B.306
C.268 D.198
D 解析:分两种情况讨论:
①若选两个国内媒体、一个国外媒体,则有CCA=90(种)不同提问方式;
②若选两个国外媒体、一个国内媒体,则有CCA=108(种)不同提问方式.
所以共有90+108=198(种)提问方式.故选D.
考点3 组合问题——基础性
(1)某单位拟安排6位员工在今年6月9日至11日值班,每天安排2人,每人值班1天.若6位员工中的甲不值9日,乙不值11日,则不同的安排方法共有( )
A.30种 B.36种
C.42种 D.48种
C 解析:若甲在11日值班,则在除乙外的4人中任选1人在11日值班,有C种选法,9日、10日有CC种安排方法,共有CCC=24(种)安排方法;
若甲在10日值班,乙在9日值班,余下的4人有CCC=12(种)安排方法;
若甲、乙都在10日值班,则共有CC=6(种)安排方法.
所以不同的安排方法共有24+12+6=42(种).
(2)现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为( )
A.232 B.252
C.472 D.484
C 解析:分两类:第一类,含有1张红色卡片,不同的取法共有CC=264(种);
第二类,不含有红色卡片,不同的取法共有C-3C=220-12=208(种).
由分类加法计数原理知,不同的取法有264+208=472(种).
组合问题的常见类型与处理方法
(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中选取.
(2)“至少”或“至多”含有几个元素的题型:若直接法分类复杂时,逆向思维,间接求解.
1.如图,∠MON的边OM上有四点A1,A2,A3,A4,ON上有三点B1,B2,B3,则以O,A1,A2,A3,A4,B1,B2,B3中三点为顶点的三角形的个数为( )
A.30 B.42
C.54 D.56
B 解析:间接法:先从这8个点中任取3个点,有C种取法,再减去三点共线的情形即可,即三角形的个数为C-C-C=42.
2.(多选题)(2020·盐城市大丰中学期中)有13名医生,其中女医生6人,现从中抽调5名医生组成医疗小组前往湖北疫区.若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为N,则下列等式能成为N的算式的是( )
A.C-CC
B.CC+CC+CC+C
C.C-CC-C
D.CC
BC 解析:13名医生,其中女医生6人,男医生7人.
利用直接法,2男3女:CC;3男2女:CC;4男1女:CC;5男:C,所以N=CC+CC+CC+C.
利用间接法:13名医生,任取5人,减去抽调4名女医生和5名女医生的情况,即N=C-CC-C.
所以能成为N的算式的是BC.故选BC.
考点4 排列与组合的综合应用——综合性
(1)(2020·滨海新区大港一中高三模拟)从5名学生中选出4名分别参加数学、物理、化学、生物四科竞赛,其中甲不能参加生物竞赛,则不同的参赛方案种数为( )
A.48 B.72
C.90 D.96
D 解析:甲不参加生物竞赛,则安排甲参加另外3场比赛或甲学生不参加任何比赛.
①当甲参加另外3场比赛时,共有C·A=72(种)选择方案;②当甲不参加任何比赛时,共有A=24(种)选择方案.故不同的参赛方案有72+24=96(种).
(2)(2020·临沂市临沭县高三模拟)某旅游公司为了推出新的旅游产品项目,派出五名工作人员前往重庆的三个网红景点——洪崖洞夜景、轻轨穿楼、长江索道进行团队游的可行性调研.若每名工作人员只去一个景点,每个景点至少有一名工作人员前往,其中工作人员甲、乙需要到同一景点调研,则不同的人员分配方案种数为( )
A.18 B.36
C.54 D.72
B 解析:若甲、乙一起(无其他人)有CA=18(种)方案;
若甲、乙与另一人一起(三人一起)有CA=18(种)方案.所以不同的人员分配方案有18+18=36(种).故选B.
(3)有七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两名同学要站在一起,则不同的站法有( )
A.240种 B.192种
C.96种 D.48种
B 解析:当丙和乙在甲的左侧时,共有ACAA=96(种)站法.同理,当丙和乙在甲的右侧时,也有96种站法,所以不同的站法共有192种.
求解排列、组合应用问题的六种主要方法
直接法 | 把符合条件的排列数直接列式计算 |
优先法 | 优先安排特殊元素或特殊位置 |
捆绑法 | 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列 |
插空法 | 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中 |
定序问 题除法处理 | 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列 |
间接法 | 正难则反、等价转化的方法 |
1.(2020·杭州市高三二模)有来自甲、乙、丙三个班级的5名同学站成一排照相,其中甲班2人,乙班2人,丙班1人,则仅有一个班级的同学相邻的站法种数是( )
A.96 B.48
C.36 D.24
B 解析: 由题意知,可以是甲班的2名同学相邻,也可以是乙班的2名同学相邻,相邻的2名同学和丙班的1名同学站队,共有CAA种站法.再将另外一个班级的2名同学进行插空,共有A种站法.由分步乘法计数原理知,仅有一个班级的同学相邻的站法种数是CAAA=48.故选B.
2.(2020·泸州市高三三模)某中学学生会体育部共有5人,现需从体育部选派4人,分别担任拔河比赛的裁判、记录结果、核查人数、维持纪律四项工作,每人只担任其中一项工作,其中甲没有担任裁判工作,则不同的工作安排方式共有
( )
A.120种 B.48种
C.96种 D.60种
C 解析:从5人中选4人担任4项不同工作,有A种方法.若甲担任裁判工作,再从另外4人中选3人担任3项不同工作,有A种方法,则符合题意的工作安排方式共有A-A=96(种).故选C.
3.安排A,B,C,D,E,F 六位义工照顾甲、乙、丙三位老人,每两位义工照顾一位老人,考虑到义工与老人的住址距离问题,不安排义工A照顾老人甲,不安排义工B照顾老人乙,求不同的安排方法种数.
解:(方法一)先按A分类,兼顾考虑B,分类如下.
A照顾乙,B照顾甲,有安排方法CC=12(种);
A照顾乙,B照顾丙,有安排方法CC=12(种);
A照顾丙,B照顾甲,有安排方法CC=12(种);
A照顾丙,B照顾丙,有安排方法C=6(种).
综上分析可得,不同的安排方法共有12+12+12+6=42(种).
(方法二:间接法)六位义工照顾三位老人,每两位义工照顾一位老人,共有安排方法CC=90(种).
其中A照顾老人甲的情况有CC=30(种);
B照顾老人乙的情况有CC=30(种);
A照顾老人甲,同时B照顾老人乙的情况有CC=12(种).
所以符合题意的安排方法有90-30-30+12=42(种).
人教B版高考数学一轮总复习第8章第7节抛物线学案: 这是一份人教B版高考数学一轮总复习第8章第7节抛物线学案,共13页。
人教B版高考数学一轮总复习第8章第6节双曲线学案: 这是一份人教B版高考数学一轮总复习第8章第6节双曲线学案,共14页。
人教B版高考数学一轮总复习第8章第1节直线方程学案: 这是一份人教B版高考数学一轮总复习第8章第1节直线方程学案,共12页。












