北师大版八年级上册第三章 位置与坐标2 平面直角坐标系精品达标测试

这是一份北师大版八年级上册第三章 位置与坐标2 平面直角坐标系精品达标测试，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题3.2 平面直角坐标系（基础篇）（专项练习）
一、单选题
1．如图，方格纸上有M，N两点，若以N为原点建立平面直角坐标系，则点M的坐标为（3，4）；若以M点为原点建立平面直角坐标系，则点N的坐标为（       ）

A．（－3，－4） B．（4，0）
C．（0，－2） D．（2，0）
2．若点P是第二象限内的点，且点P到x轴的距离是2，到y轴的距离是3，则点P的坐标是 （       ）
A．(2，3) B．(2，－3) C．(－3，2) D．(3，－2)
3．在平面直角坐标系中，点所在的象限为（       ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．在平面直角坐标系中，点在第四象限内，则的取值可以是（　　）
A．1 B． C．0 D．2或﹣2
5．下列说法不正确的是（       ）
A．点一定在第二象限 B．点到轴的距离为2
C．若中，则点在轴上 D．若在轴上，则
6．平面直角坐标系中，点，，经过点A的直线轴，点C是直线a上的一个动点，当线段BC的长度最短时，点C的坐标为（       ）．
A． B． C． D．
7．已知点P的坐标为，且P到两坐标轴的距离相等，则点P的坐标为（       ）
A． B． C． D．或
8．已知，则点在第（       ）象限．
A．一 B．二 C．三 D．四
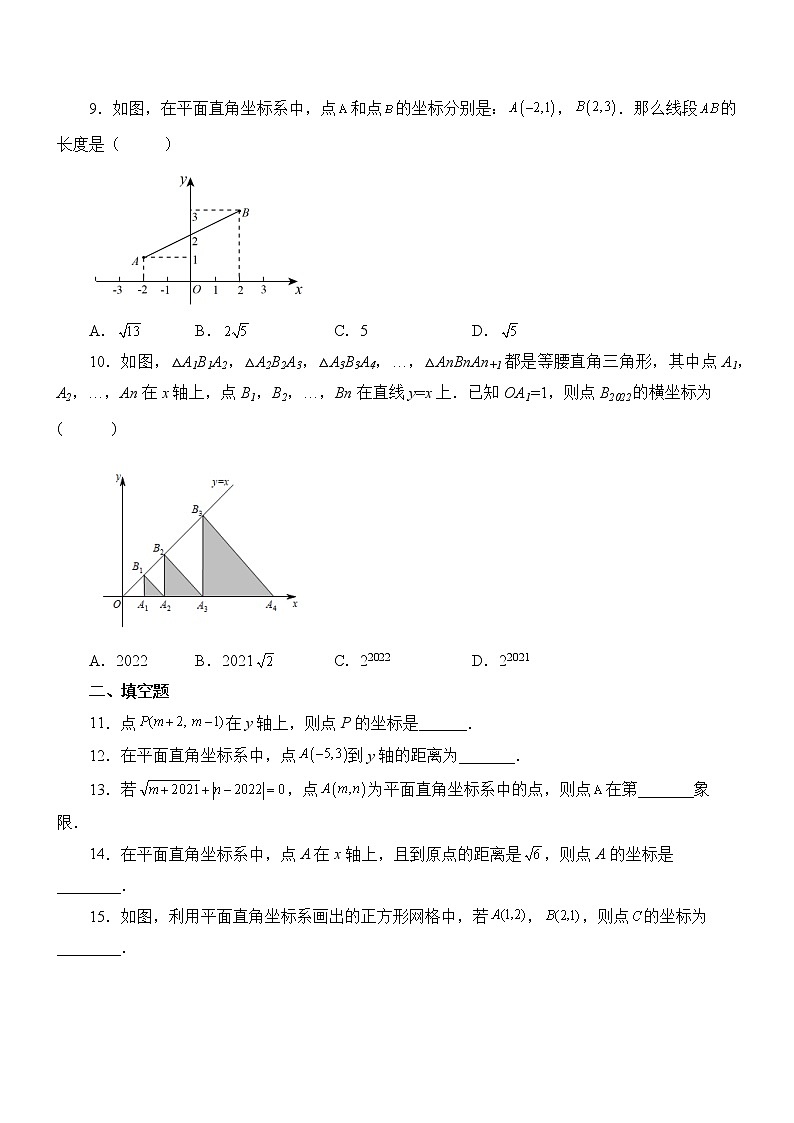
9．如图，在平面直角坐标系中，点和点的坐标分别是：，．那么线段的长度是（       ）

A． B． C．5 D．
10．如图，△A1B1A2，△A2B2A3，△A3B3A4，…，△AnBnAn+1都是等腰直角三角形，其中点A1，A2，…，An在x轴上，点B1，B2，…，Bn在直线y=x上．已知OA1=1，则点B2022的横坐标为(        )

A．2022 B．2021 C．22022 D．22021
二、填空题
11．点在y轴上，则点P的坐标是______．
12．在平面直角坐标系中，点到y轴的距离为_______．
13．若，点为平面直角坐标系中的点，则点在第_______象限．
14．在平面直角坐标系中，点A在x轴上，且到原点的距离是，则点A的坐标是________．
15．如图，利用平面直角坐标系画出的正方形网格中，若，，则点的坐标为________．

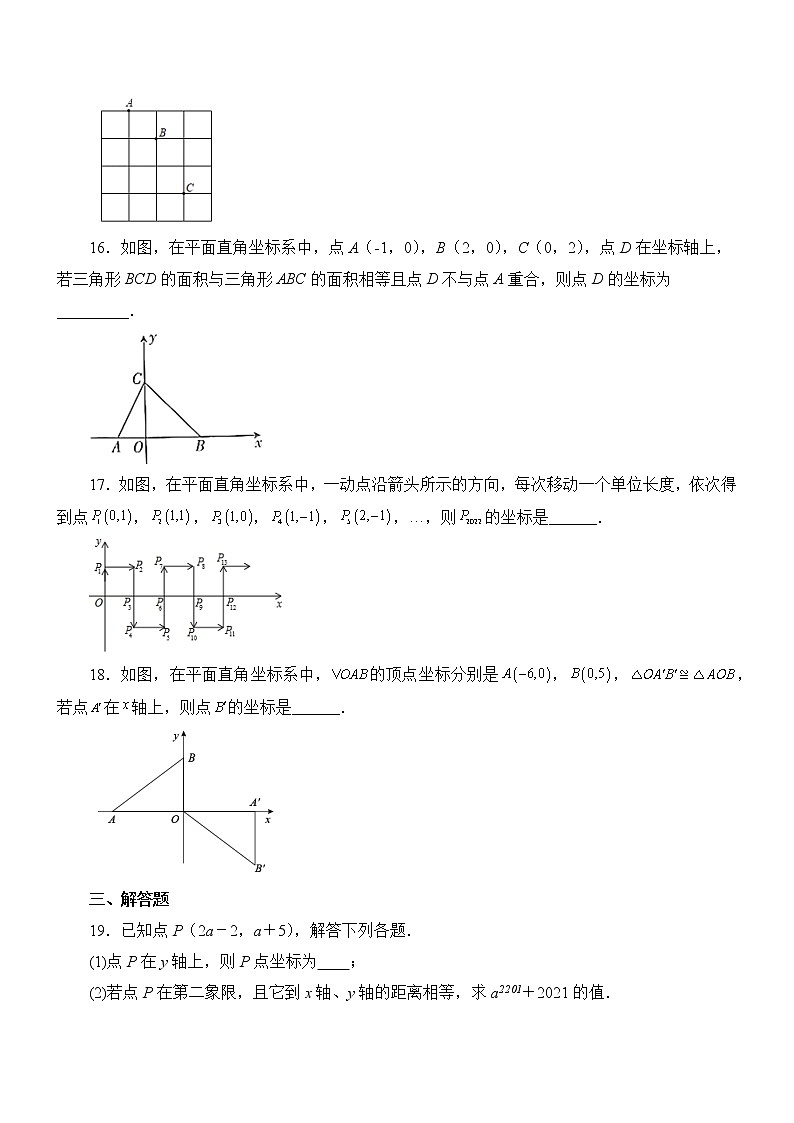
16．如图，在平面直角坐标系中，点A（-1，0），B（2，0），C（0，2），点D在坐标轴上，若三角形BCD的面积与三角形ABC的面积相等且点D不与点A重合，则点D的坐标为_________．

17．如图，在平面直角坐标系中，一动点沿箭头所示的方向，每次移动一个单位长度，依次得到点，，，，，…，则的坐标是______．

18．如图，在平面直角坐标系中，的顶点坐标分别是，，，若点在轴上，则点的坐标是______．

三、解答题
19．已知点P（2a－2，a＋5），解答下列各题．
(1)点P在y轴上，则P点坐标为　　；
(2)若点P在第二象限，且它到x轴、y轴的距离相等，求a2201＋2021的值．






20．已知：在平面直角坐标系中．
(1)若点Р在第三象限的角平分线上，求Р点坐标；
(2)若点Р在第四象限，且到两坐标轴的距离之和为9，求Р点坐标．






21．在平面直角坐标系中，有点A（-2，a+3），B（b，b-3）．
(1)当点A在第二象限的角平分线上时，求a的值；
(2)当点B到x轴的距离是它到y轴的距离2倍时，求点B的坐标．








22．如图，建立平面直角坐标系，使点，的坐标分别为和，写出点，，，，的坐标，并指出它们所在的象限．






23．如图，在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t秒．

(1)直接写出点B和点C的坐标：B　 　，C　 　；
(2)当点P运动时，用含t的式子表示线段AP的长；
(3)若x轴上有一点D（2，0），连接PD，AD．是否存在这样的t值，使得三角形APD的面积是四边形ABOC面积的？若存在，请求出t的值；若不存在，请说明理由．





24．问题背景：（1）如图①，已知中，，，直线m经过点A，直线m，直线m，垂足分别为点D，E，易证：______+______．

（2）拓展延伸：如图②，将（1）中的条件改为：在中，，D，A，E三点都在直线m上，并且有，请求出DE，BD，CE三条线段的数量关系，并证明．
（3）实际应用：如图③，在中，，，点C的坐标为，点A的坐标为，请直接写出B点的坐标．





参考答案
1．A
略
2．C
【分析】
根据第二象限内点的坐标特点及点到坐标轴的距离定义，即可判断出点P的坐标．
解：点P到x轴的距离是2，则点P的纵坐标为±2，
点P到y轴的距离是3，则点P的横坐标为±3，
由于点P在第二象限，故P坐标为（-3，2），
故选：C．
【点拨】本题考查了各象限内点的坐标的符号特征以及点到坐标轴的距离，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
3．C
【分析】
根据第三象限内点的横纵坐标都是负数求解．
解：A（-2，-10）在第三象限，
故选：C．
【点拨】本题考查了点的坐标，数形结合思想是解题的关键．
4．B
【分析】
根据第四象限内点的纵坐标是负数，纵坐标是正数即可判断．
解：∵点是第四象限内的点，
∴a<0，
四个选项中符合题意的数是．
故选：B．
【点拨】本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
5．C
【分析】
A：第二象限的点满足（-，+），B：找出P点坐标即可确定与y轴的距离，C：xy=0，可确定x、y至少有一个为0来确定，D：根据x轴上点的坐标特征即可判定．
解：A：＜0，＞0，本选项说法正确；
B：P点到y轴距离是2，本选项说法正确；
C：xy=0，得到x、y至少有一个为0，P可能在x轴上，也可能在y轴上，本选项说法错误；
D：点P在x轴上，则y=0，本选项说法正确.
故选：C．
【点拨】本题考查坐标上点的特征．确定各个象限的点和坐标轴上点的特征是解决本题的关键．
6．D
【分析】
根据题意画出图形，根据直线a//x轴，得到直线a为直线y= 2，根据垂线段最短即可得出答案．
解：
如图，∵直线a// x轴，
∴直线a为直线y= 2，
当BC⊥a时，线段BC最短，
∴点C的坐标为(2， 2)．
故选： D．
【点拨】本题考查了坐标与图形性质，掌握平行于x轴的坐标的特点，以及垂线段最短是解题的关键．
7．D
【分析】
由点P到两坐标轴的距离相等，建立绝对值方程，再解方程即可得到答案．
解： 点P到两坐标轴的距离相等，
，
或，
当时，
解得：，
；
当时，
解得：，
；
综上分析可知，的坐标为：或，故D正确．
故选：D．
【点拨】本题考查的是平面直角坐标系内点的坐标特点，点到坐标轴的距离与坐标的关系，一元一次方程的解法，掌握以上知识是解题的关键．
8．D
【分析】
先判断横坐标和纵坐标的符号，再根据各象限内点的坐标的符号特征即可得到答案．
解：∵，
∴＞0，
∵，
∴a－2＜0，
∴＜0，
∴点的横坐标是正数，纵坐标是负数，
∴点在第四象限．
故选：D
【点拨】此题考查了平面直角坐标系各象限内点的坐标的符号特征、二次根式的性质和化简等知识，记住各象限内点的坐标的符号特征是解题的关键．
9．B
【分析】
过点B作BC⊥x轴于C，过点A作AD⊥BC于D，由A、B坐标求出AD、BD长，再由勾股定理求解即可．
解：如图，过点B作BC⊥x轴于C，过点A作AD⊥BC于D，

∵A(-2,1)，B(2,3)，
∴AD=[2-（-2）]=4，BD=3-1=2,
由勾股定理，得AB=，
故选：B．
【点拨】本题考查坐标与图形性质，勾股定理，构造直角三角形，利用勾股定理求解是解题的关键．
10．D
【分析】
OA1=1=20，利用y=x，逐次求出A1B1=1，OA2=2=21，OA3=1+1+2=4=22，OA4=8=23，即可求解．
解：OA1=1=20，
则A1B1=1，OA2=2=21，
则A2B2=2，则A2A3=2，则OA3=1+1+2=4=22，
A3B3=OA3=4，则OA4=8=23，
…
则OA2022=22021，
故选：D．
【点拨】本题考查的是一次函数图象上点的坐标特征，通过逐次求出OA2=21、OA3=22、OA4=23…，通过找规律求解即可．
11．
【分析】
根据直角坐标系中坐标的性质，得通过求解方程得到m的值，再代入到坐标中计算，即可得到答案．
解：∵点在y轴上，



∴点P的坐标是
故答案为：
【点拨】本题主要考查了直角坐标系，一元一次方程的知识，解题的关键是熟练掌握直角坐标系中坐标的性质．
12．5
【分析】
根据点到y轴的距离是横坐标的绝对值，可得答案．
解：点A（-5，3）到y轴的距离是：|-5|=5．
故答案为：5．
【点拨】本题考查了点的坐标，正确掌握点的坐标特点是解决的关键．
13．二
【分析】
根据非负数的意义可求出m、n的值，再根据点A坐标的特征判定所在的象限．
解：∵
∴m+2021=0，n-2020=0，
即m=-2021，n=2020，
∴点A（-2021，2020），
∴点A在第二象限．
故答案为：二．
【点拨】本题考查非负数的性质，点的坐标，理解绝对值，算术平方根的性质以及点的坐标的特征是正确解答的关键．
14．（－，0）或（，0）
【分析】
根据x轴上的点的纵坐标为0，分点A在原点的左边与右边两种情况解答．
解：∵点A在x轴上，且到原点的距离为，
∴点A在原点左边时，坐标为（-，0），
在原点右边时，坐标为（，0），
点A的坐标为（-，0）或（，0）；
故答案为：（-，0）或（，0）．
【点拨】本题考查了坐标与图形的性质，熟练掌握平面直角坐标系中的点的坐标特点是解题的关键．
15．
【分析】
根据A、B两点坐标找到原点坐标即可解答；
解：由，，可得平面直角坐标系如下图：

∴C点坐标（3，-1），
【点拨】本题考查了平面直角坐标系，掌握坐标的定义是解题关键．
16．（5，0）或（0，5）或（0，-1）
【分析】
分为点D在x轴上和y轴上两种情况，依据三角形的面积公式求解即可．
解：∵点A（-1，0），B（2，0），C（0，2），
∴OA=1，OB=2，OC=2，
∴S△ABC=AB×OC=3，
当点D在x轴上时，S△BCD=DB•OC=DB=3．
∴D的坐标为（5，0）或（-1，0）；
（-1，0）与点A重合，不合题意，舍去，
当点D在y轴上时，S△BCD=CD•OB=CD=3．
∴点D的坐标为（0，5）或（0，-1）．
综上所述，点D的坐标为（5，0）或（0，5）或（0，-1）．
故答案为：（5，0）或（0，5）或（0，-1）．
【点拨】本题主要考查的是三角形的面积，坐标与图形的性质，分类讨论是解题的关键．
17．（674，0）
【分析】
该点按6次一循环的规律移动，用2022除以6，再确定商和余数即可．
解：由题意该点按“上→右→下→下→右→上”的方向每6次一循环移动的规律移动，且每移动一个循环向右移动2个单位长度可得，
2022÷6=337，
∴点P2022的横坐标为2×336+2=674，点P2022的纵坐标是0，
故答案为：（674，0）．
【点拨】此题考查了点的坐标方面规律问题的解决能力，关键是能准确理解题意确定出点移动的规律．
18．(6,-5)
【分析】
根据全等三角形的性质和点的坐标得出OA=OA′=6，OB=A′B′=5，即可得出答案．
解：∵A（-6，0），B（0，5），△OA′B′≌△OAB，
∴OA=OA′=6，OB=A′B′=5，
∴点B′的坐标是（6，-5），
故答案为：（6，-5）．
【点拨】本题考查了坐标与图形性质，全等三角形的性质的应用，解此题的关键是求出OA=OA′=6，OB=A′B′=5．
19．(1)P（0，6）(2)2020
【分析】
（1）根据y轴上的点的横坐标为0列式求出a的值，然后求出P点纵坐标即可；
（2）根据第二象限内点的坐标特点及点P到x轴、y轴的距离相等列式求出a的值，再代入代数式计算即可．
（1）解：∵点P在y轴上，∴2a－2＝0，∴a＝1，∴a＋5＝6，∴P（0，6）；
（2）∵点P在第二象限，∴2a－2＜0， a＋5＞0，∵点P到x轴、y轴的距离相等，∴，∴－（2a－2）＝ a＋5，解得：a＝－1，∴a2201＋2021＝（－1） 2201＋2021＝2020．
【点拨】本题主要考查了平面直角坐标系，掌握坐标轴上点的坐标特征及各象限内点的坐标特点是解题的关键．
20．(1)(2)P（8，-1）
【分析】
（1）根据第三象限角平分线上的点的特征，可得答案；
（2）根据到两坐标轴的距离之和可得方程，解方程可得答案．
(1)解：由题意，得
4x=x-3，
解得x=-1
∴．
(2)解：由题意，得
4x+[-（x-3）]=9，
则3x=6，
解得x=2，
此时点P的坐标为（8，-1）．
【点拨】本题考查了点的坐标以及一元一次方程的应用，理解题意得出方程是解题关键．
21．(1)a=-1；(2)点B的坐标为（-3，-6）或（1，-2）．
【分析】
（1）根据第二象限角平分线上的点的横坐标与纵坐标互为相反数列方程求解即可；
（2）根据题意列出绝对值方程，求出b的值，再求出点B的坐标．
(1)解：由题意，得a+3=2，
解得a=-1；
(2)解：由题意，得|b-3|=2|b|，
解得b=-3或b=1，
当b=-3时，点B（-3，-6）在第三象限，
当b=1时，点B（1，-2）在第四象限．
综上，点B的坐标为（-3，-6）或（1，-2）．
【点拨】本题考查了点的坐标，主要利用了第二象限角平分线上点的坐标特征以及点到坐标轴的距离的表示．
22．见分析．
【分析】
以点B为坐标原点建立直角坐标系，然后写出各点的坐标即可．
解：平面直角坐标系如图所示．，，，，．点在第二象限，其余各点都在第一象限．

【点拨】本题考查坐标与图形的性质，是基础考点，掌握相关知识是解题关键．
23．(1)（0，6）；（8，0）(2)AP=8-2t（0≤t＜4）或AP=2t-8（4≤t≤7）．
(3)存在，t的值为3或5
【分析】
（1）根据题意即可得到结论；
（2）当点P在线段BA上时，根据A（8，6），B（0，6），C（8，0），得到AB=8，AC=6当点P在线段AC上时，于是得到结论；
（3）当点P在线段BA上时，当点P在线段AC上时，根据三角形的面积公式即可得到结论．
(1)解：∵AB⊥y轴于B，AC⊥x轴于C，点A（8，6），
∴∠ABO=∠BOC=∠ACO=90°，
∴四边形ABOC是长方形，
∴AB=8，AC=6，
∴B（0，6），C（8，0），
故答案为：（0，6），（8，0）；
(2)解：当点P在线段BA上时，
由A（8，6），B（0，6），C（8，0）可得：AB=8，AC=6
∵AP=AB-BP，BP=2t，
∴AP=8-2t（0≤t＜4）；
当点P在线段AC上时，
∴AP=2t-8（4≤t≤7）．
(3)解：存在；
由题意，四边形ABOC的面积=AB•AC=8×6=48．
当点P在线段BA上时，

∵三角形APD的面积=AP•AC，
∴×（82t）×6=×48，
解得：t=3；
当点P在线段AC上时，

∵三角形APD的面积=AP•CD，CD=82=6，
∴×（2t8）×6=×48，
解得：t=5．
综上所述：当t的值为3或5时，三角形APD的面积是四边形ABOC面积的．
【点拨】本题考查了坐标与图形性质，长方形的性质，三角形面积的计算，正确的作出图形是解题的关键．
24．（1）BD；CE；证明见详解；（2）DE=BD+CE；证明见详解；（3）点B的坐标为．
【分析】
（1）根据全等三角形的判定和性质得到，，结合图形解答即可；
（2）根据三角形内角和定理、平角的定义证明，证明，根据全等三角形的性质得到，，结合图形解答即可；
（3）根据，得到，，根据坐标与图形性质解答即可．
（1）证明：∵，，
∴，
∵，
∴，
∵，
∴，
在和中
，
∴，
∴，，
∴，
即：，
故答案为：BD；CE；
（2）解：数量关系： ，
证明：在中，，
∵，，
∴，
在和中，

∴，
∴，，
∴；
（3）解：如图，作轴于E，轴于F，

由（1）可知，，
∴，，
∴，
∴点B的坐标为．
【点拨】本题考查的是全等三角形的判定和性质、坐标与图形性质，掌握全等三角形的判定定理和性质定理是解题的关键．