数学八年级上册12.2 三角形全等的判定同步练习题

这是一份数学八年级上册12.2 三角形全等的判定同步练习题，文件包含第10课直角三角形全等判定教师版docx、第10课直角三角形全等判定学生版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

第10课 直角三角形全等判定

知识精讲
知识点01 判定直角三角形全等的一般方法
由三角形全等的条件可知，对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，这两个直角三角形就全等了.这里用到的是“AAS”，“ASA”或“SAS”判定定理.

知识点02 判定直角三角形全等的特殊方法——斜边，直角边定理

在两个直角三角形中，有斜边和一条直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”）.这个判定方法是直角三角形所独有的，一般三角形不具备.
要点诠释：
（1）“HL”从顺序上讲是“边边角”对应相等，由于其中含有直角这个特殊条件，所以三角形的形状和大小就确定了.
（2）判定两个直角三角形全等的方法共有5种：SAS、ASA、AAS、SSS、HL.证明两个直角三角形全等，首先考虑用斜边、直角边定理，再考虑用一般三角形全等的证明方法.
（3）应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件，书写时必须在两个三角形前加上“Rt”.

能力拓展

考法01 直角三角形全等的判定——“HL”

【典例1】判断满足下列条件的两个直角三角形是否全等，不全等的画“×”，全等的注明理由：
（1）一个锐角和这个角的对边对应相等；（ ）
（2）一个锐角和斜边对应相等； （ ）
（3）两直角边对应相等； （ ）
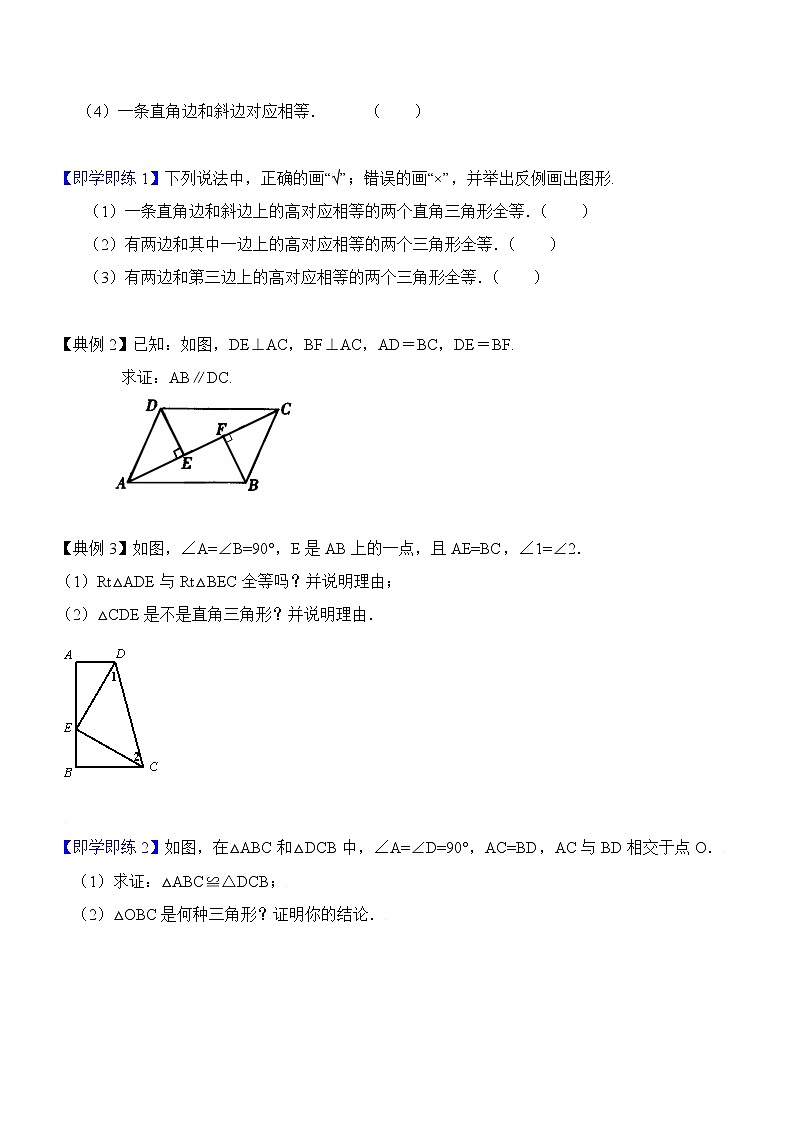
（4）一条直角边和斜边对应相等． （ ）
【答案】（1）全等，“AAS”；（2）全等，“AAS”；（3）全等，“SAS”；（4）全等，“HL”.
【解析】理解题意，画出图形，根据全等三角形的判定来判断.
【总结升华】直角三角形全等可用的判定方法有5种：SAS、ASA、AAS、SSS、HL.

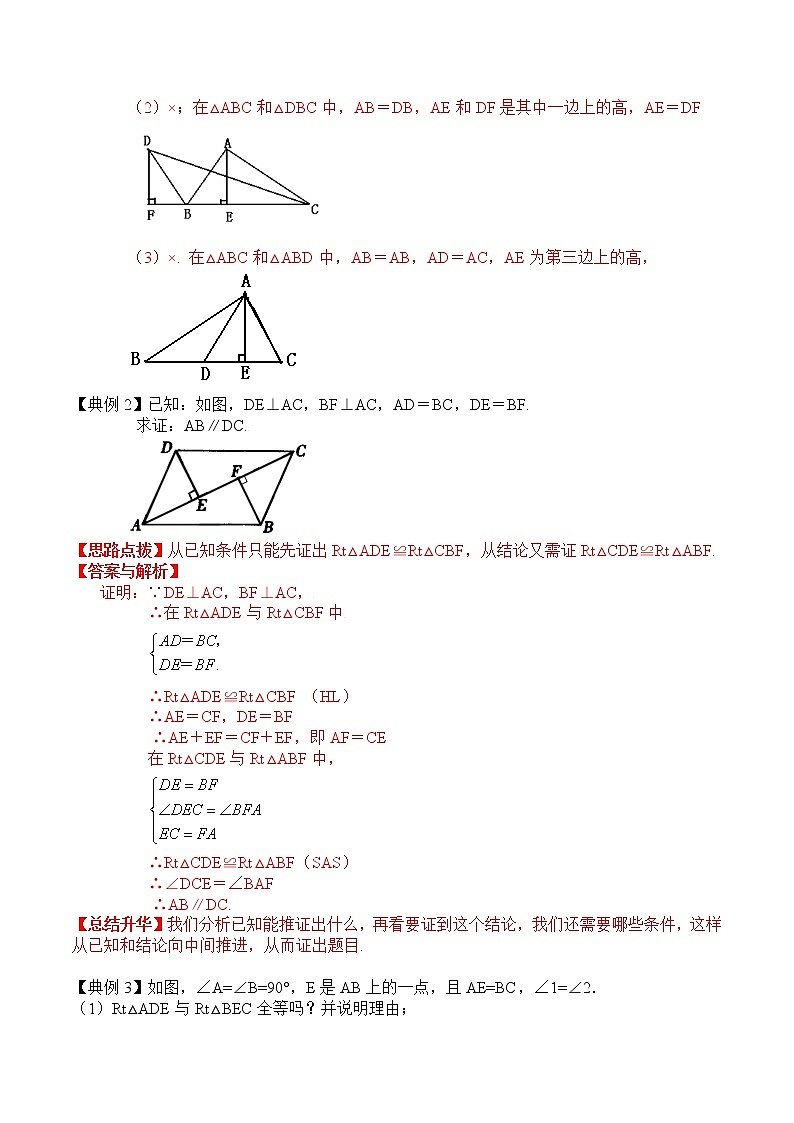
【即学即练1】下列说法中，正确的画“√”；错误的画“×”，并举出反例画出图形.
（1）一条直角边和斜边上的高对应相等的两个直角三角形全等．（ ）
（2）有两边和其中一边上的高对应相等的两个三角形全等．（ ）
（3）有两边和第三边上的高对应相等的两个三角形全等．（ ）
【答案】（1）√；
（2）×；在△ABC和△DBC中，AB＝DB，AE和DF是其中一边上的高，AE＝DF

（3）×. 在△ABC和△ABD中，AB＝AB，AD＝AC，AE为第三边上的高，

【典例2】已知：如图，DE⊥AC，BF⊥AC，AD＝BC，DE＝BF.
求证：AB∥DC.

【思路点拨】从已知条件只能先证出Rt△ADE≌Rt△CBF，从结论又需证Rt△CDE≌Rt△ABF.
【答案与解析】
证明：∵DE⊥AC，BF⊥AC，
∴在Rt△ADE与Rt△CBF中

∴Rt△ADE≌Rt△CBF （HL）
∴AE＝CF，DE＝BF
∴AE＋EF＝CF＋EF，即AF＝CE
在Rt△CDE与Rt△ABF中，

∴Rt△CDE≌Rt△ABF（SAS）
∴∠DCE＝∠BAF
∴AB∥DC.
【总结升华】我们分析已知能推证出什么，再看要证到这个结论，我们还需要哪些条件，这样从已知和结论向中间推进，从而证出题目.

【典例3】如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．
（1）Rt△ADE与Rt△BEC全等吗？并说明理由；
（2）△CDE是不是直角三角形？并说明理由．

【思路点拨】（1）根据∠1=∠2，得DE=CE，利用“HL”可证明Rt△ADE≌Rt△BEC；
（2）是直角三角形，由Rt△ADE≌Rt△BEC得，∠3=∠4，从而得出∠4+∠5=90°，则△CDE是直角三角形．
【答案与解析】
解：（1）全等，理由是：
∵∠1=∠2，
∴DE=CE，
∵∠A=∠B=90°，AE=BC，
∴Rt△ADE≌Rt△BEC(HL)；
（2）是直角三角形，理由是：
∵Rt△ADE≌Rt△BEC，
∴∠3=∠4，
∵∠3+∠5=90°，
∴∠4+∠5=90°，
∴∠DEC=90°，
∴△CDE是直角三角形．
【总结升华】考查了直角三角形的判定，全等三角形的性质，做题时要结合图形，在图形上找条件．

【即学即练2】如图，在△ABC和△DCB中，∠A=∠D=90°，AC=BD，AC与BD相交于点O．
（1）求证：△ABC≌△DCB；
（2）△OBC是何种三角形？证明你的结论．

【答案】证明：（1）因为∠A=∠D=90°，所以△ABC和△DCB都是直角三角形，
在Rt△ABC和Rt△DCB中，

∴Rt△ABC≌Rt△DCB（HL）；
（2）△OBC是等腰三角形. 理由如下：
∵Rt△ABC≌Rt△DCB，
∴∠ACB=∠DCB，
∴OB=OC
∴△OBC是等腰三角形.
【典例4】如图，△ABC中，∠ACB＝90°，AC＝BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D.
（1）求证：AE＝CD；
（2）若AC＝12，求BD的长.

【答案与解析】
（1）证明：∵DB⊥BC，CF⊥AE，
∴∠DCB＋∠D＝∠DCB＋∠AEC＝90°．
∴∠D＝∠AEC．
又∵∠DBC＝∠ECA＝90°，
且BC＝CA，
∴△DBC≌△ECA（AAS）．
∴AE＝CD．
（2）解：由（1）得AE＝CD，AC＝BC，
∴△CDB≌△AEC（HL）
∴BD＝EC＝BC＝AC，且AC＝12．
∴BD＝6．
【总结升华】三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件.


分层提分


题组A 基础过关练
1．下列语句中不正确的是（ ）
A．斜边和一锐角对应相等的两个直角三角形全等
B．有两边对应相等的两个直角三角形全等
C．有两个锐角相等的两个直角三角形全等
D．有一直角边和一锐角对应相等的两个直角三角形全等
【答案】C
【分析】
根据直角三角形的判定条件直接进行解答即可．
【详解】
A、由斜边和一锐角对应相等，结合直角相等，故可判定这两个直角三角形全等，故不符合题意；
B、如果这两个直角三角形的两边是斜边与直角边对应相等，则根据“HL”可判定，如果是这两个直角三角形的两条直角边对应相等，则可根据“SAS”判定全等，故不符合题意；
C、有两个锐角相等的两个直角三角形是不能判定全等，因为没有边的对应关系，故符合题意；
D、有一直角边和一锐角对应相等的两个直角三角形可根据“ASA”或“AAS”判定，故不符合题意；
故选C．
【点睛】
本题主要考查直角三角形的判定，熟练掌握直角三角形的判定条件是解题的关键．
2．不能使两个直角三角形全等的条件是（ ）
A．斜边、直角边对应相等
B．两直角边对应相等
C．一锐角和斜边对应相等
D．两锐角对应相等
【答案】D
【解析】根据各选项提供的已知条件，结合直角三角形全等的判定方法，对选项逐一验证，选项D只有两个锐角对应相等是不符合直角三角形判定方法的，所以不能判定三角形全等．
解：A、符合AAS，正确；
B、符合HL，正确；
C、符合ASA，正确；
D、因为判定三角形全等必须有边的参与，错误．
故选D．
3．在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列条件不能判定Rt△ABC≌Rt△DEF的是（　　）
A．AC＝DF，∠B＝∠E B．∠A＝∠D，∠B＝∠E
C．AB＝DE，AC＝DF D．AB＝DE，∠A＝∠D
【答案】B
【分析】
本题主要考查两个三角形全等的条件：两边夹一角(SAS)，两角夹一边(ASA)，两角对一边(AAS)，三条边(SSS)，HL.且要明确满足下列条件之一的两个三角形是全等的：
(1)有两边和第三边上的中线对应相等；
(2)有两边和第三边上的高对应相等；
(3)有两边和第三边上的角平分线对应相等；
【详解】
解：A、∵在Rt△ABC和Rt△DEF中

∴Rt△ABC≌Rt△DEF（AAS），故本选项不符合题意；
B、在Rt△ABC和Rt△DEF中，根据∠A＝∠D、∠C＝∠F\、∠B＝∠E不能推出两三角形全等，故本选项符合题意；
C、∵在Rt△ABC和Rt△DEF中

∴Rt△ABC≌Rt△DEF（HL），故本选项不符合题意；
D、∵在Rt△ABC和Rt△DEF中

∴Rt△ABC≌Rt△DEF（AAS），故本选项不符合题意；
故选：B．
【点睛】
此题考查直角三角形全等的判定，解题关键在于掌握判定定理.
4．如图，∠B=∠D=90°，BC=CD，∠1=40°，则∠2=（　　）

A．40° B．50° C．60° D．75°
【答案】B
【解析】
【分析】
由∠B=∠D=90°，可知△ABC和△ADC是直角三角形，这样在两三角形中，利用“HL”可判定△ABC≌△ADC；根据全等三角形的性质可得∠DAC的度数，结合直角三角形两锐角互余,即可求出∠2的度数.
【详解】
∵∠B=∠D=90°，
∴△ABC和△ADC是直角三角形.
在Rt△ABC和Rt△ADC中，BC=DC，AC=AC，
∴△ABC≌△ADC，
∴∠DAC=∠1=40°，
∴∠2=50°.
故选:B.
【点睛】
考查全等三角形的判定与性质，掌握全等三角形的判定定理是解题的关键.
5．在两个直角三角形中,若有一组对角对应相等,一组对边对应相等,则这两个直角三角形( )
A．一定全等 B．一定不全等 C．可能全等 D．以上都不是
【答案】C
【解析】
【分析】
解：根据两个直角三角形中,若有一组对角（非直角）对应相等,一组对边对应相等,则这两个直角三角形全等可得.
【详解】
当两个直角三角形中,若有一组对角（非直角）对应相等,一组对边对应相等,又两直角对应相等，则这两个直角三角形全等（AAS）；
当两个直角三角形中,若有一组对角（直角）对应相等,一组对边对应相等；只有一组角，一组边对应相等，则不能判定两三角形是否全等.
故选：C
【点睛】
本题考查两直角三角形全等的判定方法，注意条件当中对对应角的限定条件.
6．下列命题中不正确的是（ ）
A．斜边对应相等的两个等腰直角三角形全等
B．有两条直角边对应相等的两个直角三角形全等
C．有一条边相等的两个等腰三角形全等
D．有一条直角边和斜边上的中线对应相等的两个直角三角形全等
【答案】C
【分析】
根据全等三角形的判定方法容易得出A、B、D是真命题，C是假命题，即可得出结论．
【详解】
解：A．斜边对应相等的两个等腰直角三角形，根据两三角形全等的判定定理“AAS”得出两个三角形全等；故本选项是真命题；
B．有两条直角边对应相等的两个直角三角形全等，则其根据为“SAS”可以得出两个三角形全等，故本选项是真命题；
C．有一条边相等的两个等腰三角形全等不一定全等；故本选项是假命题；
D．有一条直角边和斜边上的中线对应相等的两个直角三角形全等根据两三角形全等的判定定理“HL”得出两个三角形全等；故本选项是真命题；      
故选：C．
【点睛】
此题主要考查了命题与定理以及全等三角形的判定方法，熟练掌握全等三角形的判定定理是解决问题的关键．
7．如图，在△ABC中AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是（ ）

A．1 B．2 C．3 D．4
【答案】A
【解析】
试题分析：本题可先根据AAS判定△AEH≌△CEB，可得出AE=CE，从而得出CH=CE﹣EH=4﹣3=1．
解：在△ABC中，AD⊥BC，CE⊥AB，
∴∠AEH=∠ADB=90°；
∵∠EAH+∠AHE=90°，∠DHC+∠BCH=90°，
∵∠EHA=∠DHC（对顶角相等），
∴∠EAH=∠DCH（等量代换）；
∵在△BCE和△HAE中
，
∴△AEH≌△CEB（AAS）；
∴AE=CE；
∵EH=EB=3，AE=4，
∴CH=CE﹣EH=AE﹣EH=4﹣3=1．
故选A．
【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA，AAS、HL，要熟练掌握并灵活应用这些方法．
8．如图所示，∠C＝∠D＝90°，添加下列条件①AC＝AD；②∠ABC＝∠ABD；③∠BAC＝∠BAD；④BC＝BD，能判定Rt△ABC与Rt△ABD 全等的条件的个数是（ ）

A．1 B．2 C．3 D．4
【答案】D
【分析】
根据已知条件与全等三角形的判定定理即可分别判断求解．
【详解】
∵∠C＝∠D＝90°，AB=AB，
∴①AC＝AD，可用HL判定Rt△ABC与Rt△ABD全等；
②∠ABC＝∠ABD，可用AAS判定Rt△ABC与Rt△ABD全等；
③∠BAC＝∠BAD，可用AAS判定Rt△ABC与Rt△ABD全等；
④BC＝BD，可用HL判定Rt△ABC与Rt△ABD全等；
故选：D．
【点睛】
此题主要考查全等三角形的判定，解题的关键是熟知全等三角形的判定定理．

题组B 能力提升练
1．如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是__________．

【答案】AC=DE
【解析】
用“HL”判定△ABC≌△DBE，已知BC=BE，再添加斜边DE=AC即可.
2．如图，已知AD是△ABC的高，E为AC上一点，BE交AD于F，且BF＝AC，FD＝CD．则∠BAD＝_______.

【答案】45°；
【分析】
由题中条件可得Rt△BDF≌Rt△ADC，推出BD=AD，推出△ABD是等腰直角三角形，由此即可解决问题．
【详解】
证明：∵AD⊥BC，
∴∠BDF=∠ADC=90°，
在Rt△BDF和Rt△ADC中，

∴Rt△BDF≌Rt△ADC（HL）
∴BD=AD，∵∠ADB=90°，
∴∠BAD=45°．
故答案为:45°.
【点睛】
本题考查了全等三角形的判定及性质，能够灵活运用其性质是解题的关键．
3．如图，E、B、F、C在同一条直线上，若∠D＝∠A＝90°，EB＝FC，AB＝DF．则ΔABC≌_____，全等的根据是_____．

【答案】△DFE HL
【分析】
先得出BE=FC，由HL可得△ABC≌△DFE，进而可得出结论．
【详解】
证明：∵BE=FC，
∴BE+BF=FC+BF，即EF=BC，
∵∠A=∠D=90°，
在RT△ABC和RT△DFE中，
，
∴△ABC≌△DFE（HL），故答案为(1). △DFE (2). HL.
【点睛】
本题考查了全等三角形的判定，熟练掌握全等三角形的判定是解题的关键．
4．判定两直角三角形全等的各种条件：（1）一锐角和一边对应相等（2）两边对应相等（3）两锐角对应相等．其中能得到两个直角三角形全等的条件是________ .
【答案】（1）和（2）
【解析】
试题分析：根据全等三角形的判定定理：AAS、SAS、ASA、SSS；直角三角形的判定地理HL对①②③逐个分析，然后即可得出答案．
解：∵（1）一锐角与一边对应相等，
可利用AAS或ASA判定两直角三角形全等，
（2）两边对应相等，可利用HL或ASA判定两直角三角形全等；
（3）两锐角对应相等，缺少对应边相等这一条件，
所以不能判定两直角三角形全等．
故（1）和（2）．
点评：此题主要考查学生对直角三角形全等的判定的理解和掌握，解答此题的关键是熟练掌握全等三角形的判定定理：AAS、SAS、ASA、SSS；直角三角形的判定定理HL，此题难度不大，是一道基础题．
5．在如图所示的4×4正方形网格中，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝_______．


【答案】315°
【解析】
试题分析：根据题意可得：∠1+∠7=∠2+∠6=∠3+∠5=90°，∠4=45°，则∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7=90°×3+45°=315°.
考点：角度的计算
6．如图,AD∥BC，AB⊥BC，CD⊥DE，CD=ED，AD=2，BC=3，则△ADE的面积为___.

【答案】1
【分析】
过点D作BC的垂线交BC于点G，过E作AD的垂线交AD的延长线于F，证得Rt△EDF≌Rt△CDG，求出GC的长，即为EF的长，然后利用三角形面积公式得解.
【详解】

如图，过点D作BC的垂线交BC于点G，过E作AD的垂线交AD的延长线于F，
∵∠EDF+∠FDC=90°
∠GDC+∠FDC=90°
∴∠EDF=∠GDC
在Rt△EDF和Rt△CDG中

∴Rt△EDF≌Rt△CDG
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1
∴
故答案为1
【点睛】
本题主要考查三角形全等的判定及性质，熟练掌握相关性质定理为解题关键.

题组C 培优拔尖练
1．如图所示，已知AB=AC，AE=AF，AE⊥EC，AF⊥BF，垂足分别是点E、F．求证：∠1=∠2．

【答案】证明见解析.
【分析】
根据HL证明Rt△AEC与Rt△AFB全等，再利用等式的性质解答即可.
【详解】
证明：∵AE⊥EC，AF⊥BF，
∴△AEC是Rt△，△AFB是Rt△，
在Rt△AEC与Rt△AFB中，
，
∴Rt△AEC≌Rt△AFB（HL），
∴∠EAC=∠FAB，
∴∠EAC﹣∠BAC=∠FAB﹣∠BAC，
即∠1=∠2．
【点睛】
本题主要考查了全等三角形的判定和性质，解题的关键是根据HL证明Rt△AEC与Rt△AFB全等.
2．如图，有一直角三角形ABC，∠C=90°，AC=10cm，BC=5cm，一条线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等．

【答案】当点P与点C重合时，△ABC才能和△APQ全等
【详解】
试题分析：本题要分情况讨论：①Rt△APQ≌Rt△CBA，此时AP=BC=5cm，可据此求出P点的位置．
②Rt△QAP≌Rt△BCA，此时AP=AC，P、C重合．
解：根据三角形全等的判定方法HL可知：
①当P运动到AP=BC时，
∵∠C=∠QAP=90°，
在Rt△ABC与Rt△QPA中，

∴Rt△ABC≌Rt△QPA（HL），
即AP=BC=5cm；
②当P运动到与C点重合时，AP=AC，
在Rt△ABC与Rt△QPA中，
，
∴Rt△QAP≌Rt△BCA（HL），
即AP=AC=10cm，
∴当点P与点C重合时，△ABC才能和△APQ全等．
点评：本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．由于本题没有说明全等三角形的对应边和对应角，因此要分类讨论，以免漏解．
3．如图，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC，若AB＝CD，试证明BD平分EF．

【答案】详见解析.
【分析】
根据已知条件证明AB=CD,AF=CF，证明 Rt△ABF≌Rt△CDE（HL）,得BF＝DE,进而证明△BFG≌△DEG（AAS），即可证明.
【详解】
证明∵DE⊥AC，BF⊥AC，
∴∠DEG＝∠BFE＝90°,
∵AE＝CF，AE＋EF＝CF＋EF,即AF＝CE． 
在Rt△ABF和Rt△CDE中，AB=CD,AF=CF，
∴Rt△ABF≌Rt△CDE（HL），
∴BF＝DE．
在△BFG和△DEG中，∠BFG=∠DEG,∠BGF=∠DGE，BF=DE
∴△BFG≌△DEG（AAS），
∴FG＝EG，即BD平分EF
【点睛】
本题考查了三角形全等的判定与性质,中等难度,将中点问题转化成证明全等问题是解题关键.