人教A版高考数学一轮总复习第7章第4节直线、平面垂直的判定与性质课时学案

这是一份人教A版高考数学一轮总复习第7章第4节直线、平面垂直的判定与性质课时学案，共15页。学案主要包含了教材概念·结论·性质重现，基本技能·思想·活动体验等内容，欢迎下载使用。

第四节　直线、平面垂直的判定与性质

一、教材概念·结论·性质重现
1．直线与平面垂直
(1)定义：一般地，如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直，记作l⊥α.直线l叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足．
(2)判定定理与性质定理

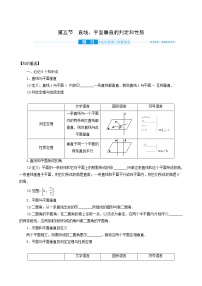
文字语言
图形语言
符号语言
判定
定理
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直

⇒l⊥α
性质
定理
垂直于同一个平面的两条直线平行

⇒a∥b


(1)线面垂直的判定定理的推论：如果在两条平行直线中，有一条直线垂直于一个平面，那么另一条直线也垂直于这个平面．
(2)直线和平面垂直的常用性质：
①若直线垂直于平面，则该直线垂直于平面内的任意直线．
②垂直于同一条直线的两个平面平行．
2．平面与平面垂直
(1)定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．
(2)判定定理与性质定理

文字语言
图形语言
符号语言
判定
定理
如果一个平面过另一个平面的垂线，那么这两个平面垂直

⇒α⊥β
性质
定理
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直

⇒l⊥α


面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可．
3．线面角与二面角
(1)直线与平面所成的角(线面角)
平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角．若一条直线垂直于平面，它们所成的角是90°.若一条直线和平面平行，或在平面内，它们所成的角是0°.直线与平面所成的角θ的取值范围是0°≤θ≤90°.
(2)二面角
①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．
②二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角．

(1)线面角的取值范围是[0°，90°]，二面角的取值范围是[0°，180°]．
(2)当线面角为90°时，线面垂直；当二面角为90°时，面面垂直．
4．常用结论
(1)若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线．
(2)若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．
(3)垂直于同一条直线的两个平面平行．
(4)一条直线垂直于两平行平面中的一个，则这一条直线与另一个平面也垂直．
(5)两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．
二、基本技能·思想·活动体验
1．判断下列说法的正误，对的打“√”，错的打“×”．
(1)若直线l与平面α内的无数条直线都垂直，则l⊥α． (×)
(2)若直线a⊥平面α，直线b∥α，则直线a与b垂直． (√)
(3)若直线a⊥α，b⊥α，则a∥b． (√)
(4)若α⊥β，a⊥β，则a∥α． (×)
(5)a⊥α，a⊂β⇒α⊥β． (√)
2．下列命题中不正确的是(　　)
A．如果平面α⊥平面β，且直线l∥平面α，则直线l⊥平面β
B．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β
C．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β
D．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥γ
A　解析：A错误，l与β可能平行或相交，或在平面β内，其余选项均正确．
3．如图，已知PA⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．

4　解析：因为PA⊥平面ABC，
所以PA⊥AB，PA⊥AC，PA⊥BC，
则△PAB，△PAC为直角三角形．
由BC⊥AC，且AC∩PA＝A，
所以BC⊥平面PAC，
从而BC⊥PC．
因此△ABC，△PBC也是直角三角形．
故图中共有4个直角三角形．
4．在三棱锥P-ABC中，点P在平面ABC中的射影为点O.
(1)若PA＝PB＝PC，则点O是△ABC的______心；
(2)若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的______心．

(1)外　(2)垂　解析：(1)如图，因为PO⊥平面ABC，连接OA，OB，OC．
在Rt△POA中，OA2＝PA2－PO2，
同理OB2＝PB2－PO2，
OC2＝PC2－PO2.
又PA＝PB＝PC，
故OA＝OB＝OC，所以O是△ABC的外心．
(2)由PA⊥PB，PA⊥PC可知PA⊥平面PBC，
所以PA⊥BC．
又PO⊥BC，
所以BC⊥平面PAO，
所以AO⊥BC，
同理BO⊥AC，CO⊥AB.
故O是△ABC的垂心．
5．已知PD垂直于正方形ABCD所在的平面，连接PB，PC，PA，AC，BD，则一定互相垂直的平面有________对．
7　解析：如图，由于PD⊥平面ABCD，故平面PAD⊥平面ABCD，平面PDB⊥平面ABCD，平面PDC⊥平面ABCD，平面PDA⊥平面PDC，平面PAC⊥平面PDB，平面PAB⊥平面PAD，平面PBC⊥平面PDC，共7对．



考点1　垂直关系的基本问题——基础性

1．已知平面α和直线a，b，若a∥α，则“b⊥a”是“b⊥α”的(　　)
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
B　解析：根据空间中直线与平面之间的位置关系，由a∥α，b⊥α，可得b⊥a.反之不成立，可能b与α相交或平行．所以“b⊥a”是“b⊥α”的必要不充分条件．
2．(多选题)已知a，b表示两条不同的直线，α，β表示两个不同的平面，下列说法正确的是(　　)
A．若a⊥α，b⊥β，α∥β，则a∥b
B．若a⊥α，b⊥β，a⊥b，则α⊥β
C．若a⊥α，a⊥b，α∥β，则b∥β
D．若α∩β＝a，a∥b，则b∥α或b∥β
ABD　解析：对于A，若a⊥α，α∥β，则a⊥β，又b⊥β，所以a∥b，故A正确；
对于B，若a⊥α，a⊥b，则b⊂α或b∥α，所以存在直线m⊂α，使得m∥b，又b⊥β，所以m⊥β，所以α⊥β.故B正确；
对于C，若a⊥α，a⊥b，则b⊂α或b∥α，又α∥β，所以b⊂β或b∥β，故C错误；
对于D，若α∩β＝a，a∥b，则b∥α或b∥β，故D正确．
3．在三棱锥S-ABC中，∠SBA＝∠SCA＝90°，△ABC是斜边AB＝a的等腰直角三角形，则以下结论：

①异面直线SB与AC所成的角为90°；
②直线SB⊥平面ABC；
③平面SBC⊥平面SAC；
④点C到平面SAB的距离是a.
其中正确的是________．(填序号)
①②③④　解析：由题意知AC⊥平面SBC，故AC⊥SB，故①正确；再根据SB⊥AC，SB⊥AB，可得SB⊥平面ABC，平面SBC⊥平面SAC，故②③正确；取AB的中点E，连接CE，可证得CE⊥平面SAB，故CE的长度即为点C到平面SAB的距离，为a，故④正确．

与线面垂直关系有关命题真假的判断方法
(1)借助几何图形来说明线面关系要做到作图快、准，甚至无须作图通过空间想象来判断．
(2)寻找反例，只要存在反例，结论就不正确．
(3)反复验证所有可能的情况，必要时要运用判定或性质定理进行简单说明．

考点2　空间角及其应用——综合性

(1)如图，在长方体ABCD-A1B1C1D1中．若AB＝AD＝2，CC1＝，则二面角C1-BD-C的大小为________．

30°　解析：如图，连接AC交BD于点O，连接C1O.

因为C1D＝C1B，O为BD的中点，所以C1O⊥BD．
因为AC⊥BD，所以∠C1OC是二面角C1-BD-C的平面角．
在Rt△C1CO中，C1C＝，CO＝AC＝，
则C1O＝2，所以sin∠C1OC＝＝.
由图可知，二面角C1­BD­C为锐二面角，
所以∠C1OC＝30°.
(2)(2020·全国卷Ⅱ)如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于点E，交AC于点F.
①证明：AA1∥MN，且平面A1AMN⊥平面EB1C1F；
②设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO＝AB，求直线B1E与平面A1AMN所成角的正弦值．

解：①因为M，N分别为BC，B1C1的中点，
所以MN∥BB1.
又AA1∥BB1，所以MN∥AA1.
在△ABC中，M为BC中点，则BC⊥AM.
又因为侧面BB1C1C为矩形，所以BC⊥BB1.
因为MN∥BB1，MN⊥BC．MN∩AM＝M，MN，AM⊂平面A1AMN，
所以BC⊥平面A1AMN.
又因为B1C1∥BC，且B1C1平面ABC，BC⊂平面ABC，所以B1C1∥平面ABC．
又因为B1C1⊂平面EB1C1F，且平面EB1C1F∩平面ABC＝EF.
所以B1C1∥EF，所以EF∥BC．
又因为BC⊥平面A1AMN，
所以EF⊥平面A1AMN.
因为EF⊂平面EB1C1F，
所以平面EB1C1F⊥平面A1AMN.
②连接NP，因为AO∥平面EB1C1F，平面AONP∩平面EB1C1F＝NP，所以AO∥NP.
根据三棱柱上下底面平行，
平面A1NMA∩平面ABC＝AM，平面A1NMA∩平面A1B1C1＝A1N，

所以ON∥AP，故四边形ONPA是平行四边形．设△ABC边长是6m(m>0)，可得ON＝AP，NP＝AO＝AB＝6m.
因为O为△A1B1C1的中心，且△A1B1C1边长为6m，
所以ON＝×6m×sin 60°＝m，故ON＝AP＝m.
因为EF∥BC，所以＝，
所以＝，解得EP＝m.
在B1C1截取B1Q＝EP＝m，故QN＝2m.
因为B1Q＝EP且B1Q∥EP，所以四边形B1QPE是平行四边形，所以B1E∥PQ.
由①知B1C1⊥平面A1AMN，故∠QPN为B1E与平面A1AMN所成角，
在Rt△QPN中，根据勾股定理可得PQ＝＝＝2m，
所以sin∠QPN＝＝＝.所以直线B1E与平面A1AMN所成角的正弦值为.

求线面角、二面角的常用方法
(1)线面角的求法：找出斜线在平面上的射影，关键是作垂线、找垂足，要把线面角转化到一个三角形中求解．
(2)二面角的大小求法：二面角的大小用它的平面角来度量．平面角的作法常见的有①定义法，②垂面法．注意利用等腰三角形和等边三角形的性质．

1．(2020·山东卷)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为(B)

A．20° B．40° C．50° D．90°
2．在四棱锥V-ABCD中，底面ABCD是边长为2的正方形，其他四个侧面都是侧棱长为的等腰三角形，则二面角V-AB-C的大小为________．
60°　解析：如图，作VO⊥平面ABCD，垂足为O，则VO⊥AB.取AB的中点H，连接VH，OH，则VH⊥AB.

因为VH∩VO＝V，所以AB⊥平面VHO，所以AB⊥OH，所以∠VHO为二面角V-AB-C的平面角．
易求VH2＝VA2－AH2＝4，所以VH＝2.
而OH＝BC＝1，所以∠VHO＝60°.
故二面角V-AB-C的大小是60°.
3．如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一动点．
(1)证明：△PBC是直角三角形；
(2)若PA＝AB＝2，当直线PC与平面ABC所成角的正切值为时，求直线AB与平面PBC所成角的正弦值．

(1)证明：因为AB是⊙O的直径，C是圆周上不同于A，B的一动点，所以BC⊥AC．
又PA⊥平面ABC，BC⊂平面ABC，
所以PA⊥BC．
因为PA∩AC＝A，PA，AC⊂平面PAC，
所以BC⊥平面PAC．
因为PC⊂平面PAC，所以BC⊥PC，
所以△PBC是直角三角形．
(2)解：如图，过点A作AH⊥PC于点H，连接BH.

因为BC⊥平面PAC，AH⊂平面PAC，
所以BC⊥AH.
又PC∩BC＝C，PC，BC⊂平面PBC，
所以AH⊥平面PBC．
因为BH⊂平面PBC，所以AH⊥BH，
所以∠ABH是直线AB与平面PBC所成的角．
因为PA⊥平面ABC，
所以∠PCA即是PC与平面ABC所成的角．
因为tan∠PCA＝＝，PA＝2，所以AC＝.
所以在Rt△PAC中，AH＝＝，
所以在Rt△ABH中，sin∠ABH＝＝＝，
即直线AB与平面PBC所成角的正弦值为.

考点3　线面垂直、面面垂直的判定与性质——应用性

考向1　线面垂直的判定与性质
如图，在四棱锥A-BCDE中，△ADE是边长为2的等边三角形，平面ADE⊥平面BCDE，底面BCDE是等腰梯形，DE∥BC，DE＝BC，BE＝DC＝2，BD＝2，M是边DE的中点，点N在BC上，且BN＝3.
(1)证明：BD⊥平面AMN；
(2)设BD∩MN＝G，求三棱锥A-BGN的体积．

(1)证明：因为△ADE是等边三角形，M是DE的中点，所以AM⊥DE.
又平面ADE⊥平面BCDE，平面ADE∩平面BCDE＝DE，所以AM⊥平面BCDE.
因为BD⊂平面BCDE，所以AM⊥BD．
因为MD＝ME＝1，BN＝3，DE∥BC，DE＝BC，
所以MDCN，所以四边形MNCD是平行四边形，所以MN∥CD．
因为BD＝2，BC＝4，CD＝2，所以BD2＋CD2＝BC2，所以BD⊥CD，所以BD⊥MN.
又AM∩MN＝M，所以BD⊥平面AMN.
(2)解：由(1)知AM⊥平面BCDE，
所以AM为三棱锥A-BGN的高．
因为△ADE是边长为2的等边三角形，所以AM＝.
易知GN＝CD＝.
又由(1)知BD⊥MN，所以BG＝＝.
所以S△BGN＝BG·NG＝××＝.
所以VA-BGN＝S△BGN·AM＝××＝.

解决线面垂直问题的关键点
(1)证明直线和平面垂直的常用方法．
①判定定理．
②平行直线的传递性(a∥b，a⊥α⇒b⊥α)．
③面面平行的性质(a⊥α，α∥β⇒a⊥β)．
④面面垂直的性质(α⊥β，α∩β＝a，l⊥a，l⊂β⇒l⊥α)．
(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．
考向2　面面垂直的判定与性质
(2021·衡水中学模拟)如图，四棱锥P-ABCD的底面ABCD为直角梯形，AB∥DC，∠ABC＝90°，∠PAB＝120°，DC＝PC＝2.PA＝AB＝BC＝1.
(1)证明：平面PAB⊥平面PBC；
(2)求四棱锥P-ABCD的体积．

(1)证明：在△PAB中，由PA＝AB＝1，∠PAB＝120°，得PB＝.
因为PC＝2，BC＝1，PB＝，
所以PB2＋BC2＝PC2，即BC⊥PB.
因为∠ABC＝90°，所以BC⊥AB，
又PB∩AB＝B，所以BC⊥平面PAB，
又BC⊂平面PBC，所以平面PAB⊥平面PBC．
(2)在平面PAB内，过点P作PE⊥AB，交BA的延长线于点E，如图所示．

由(1)知BC⊥平面PAB.
因为BC⊂平面ABCD，
所以平面PAB⊥平面ABCD．
又平面PAB∩平面ABCD＝AB，PE⊥AB，
所以PE⊥平面ABCD．
因为在Rt△PEA中，PA＝1，∠PAE＝60°，
所以PE＝.因为底面ABCD是直角梯形，所以四棱锥P-ABCD的体积为VP-ABCD＝××(1＋2)×1×＝.

解决面面垂直问题的关键点
(1)证明平面和平面垂直的方法．
①面面垂直的定义．
②面面垂直的判定定理．
(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．

1．(2021·石家庄模拟)如图，PA垂直于矩形ABCD所在的平面，则图中与平面PCD垂直的平面是(　　)

A．平面ABCD
B．平面PBC
C．平面PAD
D．平面PAB
C　解析：因为PA⊥平面ABCD，所以PA⊥CD．
因为四边形ABCD为矩形，所以CD⊥AD，
所以CD⊥平面PAD，所以平面PCD⊥平面PAD．
2．如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ABD沿对角线BD折起，记折起后点A的位置为点P，且使平面PBD⊥平面BCD．

求证：(1)CD⊥平面PBD；
(2)平面PBC⊥平面PCD．
证明：(1)因为AD＝AB，∠BAD＝90°，
所以∠ABD＝∠ADB＝45°.
又因为AD∥BC，所以∠DBC＝45°.
又∠DCB＝45°，所以∠BDC＝90°，即BD⊥CD．
因为平面PBD⊥平面BCD，平面PBD∩平面BCD＝BD，
所以CD⊥平面PBD．
(2)由CD⊥平面PBD，得CD⊥BP.
又BP⊥PD，PD∩CD＝D，所以BP⊥平面PDC．
又BP⊂平面PBC，所以平面PBC⊥平面PDC．
3．(2020·银川一模)如图，在三棱锥V-ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC，且AC＝BC＝，O，M分别为AB，VA的中点．
(1)求证：平面MOC⊥平面VAB；
(2)求三棱锥B-VAC的高．

(1)证明：因为AC＝BC，O为AB的中点，
所以OC⊥AB.
因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，OC⊂平面ABC，
所以OC⊥平面VAB.
因为OC⊂平面MOC,
所以平面MOC⊥平面VAB.
(2)解：在等腰直角三角形ACB中，AC＝BC＝，
所以AB＝2，OC＝1，
所以等边三角形VAB的面积为S△VAB＝×22×sin 60°＝，
又因为OC⊥平面VAB，所以OC⊥OM.
在△AMC中，AM＝1，AC＝，MC＝，
所以S△AMC＝×1×＝，
所以S△VAC＝2S△MAC＝.
由三棱锥B-VAC的体积与三棱锥C-VAB的体积相等，
即S△VAC·h＝S△VAB·OC,
所以h＝＝，
即三棱锥B-VAC的高为.