人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式背景图ppt课件

这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式背景图ppt课件，共54页。PPT课件主要包含了自主阅读·新知预习，合作探究·深化提能，随堂检测·内化素养，课时作业·分层自检等内容，欢迎下载使用。
知识点1　一元二次不等式[巧梳理]1．一元二次不等式的概念
2.一元二次函数的零点一般地，对于二次函数y＝ax2＋bx＋c，我们把使ax2＋bx＋c＝0的实数x叫做二次函数y＝ax2＋bx＋c的__________，一元二次方程的根是相应一元二次函数的__________
[微体验]1．下面哪些不等式是一元二次不等式(其中a，b，c，m为常数)?(1)x2>0；(2)－x－x2≤5；(3)x3＋5x－6>0；(4)mx2－5y0.解：(1)(2)符合一元二次不等式的定义，所以(1)(2)是一元二次不等式．(3)不是，因为x的最高次数为3，不符合一元一次不等式的定义．(4)不是，因为当m＝0时，它为一元一次不等式；当m≠0时，它含有二元．(5)不确定，因为当a＝0时，不符合一元二次不等式的定义．
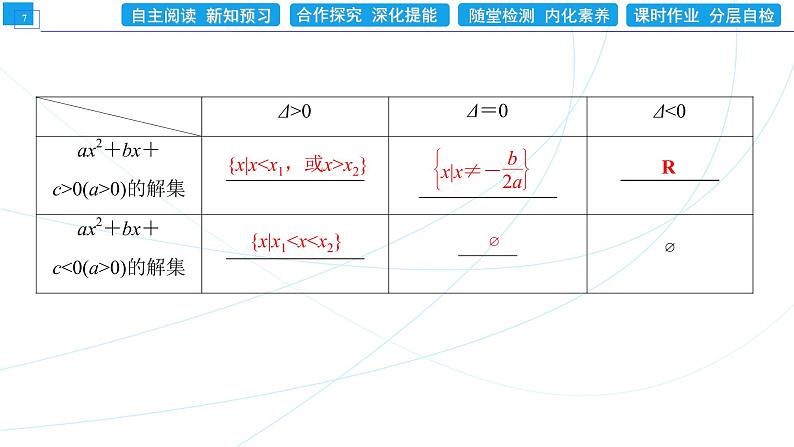
知识点2　二次函数与一元二次方程、不等式的解的关系[巧梳理]
{x|xx2}
{x|x10的解集即二次函数图象在x轴上方部分的自变量的取值范围．
一元二次不等式的解法(1)当所给的一元二次不等式是非标准形式的不等式时，应当化为标准形式．(2)一般地，当a>0时，解形如ax2＋bx＋c>0(≥0)或ax2＋bx＋c