人教A版 (2019)选择性必修 第二册第五章 一元函数的导数及其应用5.3 导数在研究函数中的应用课堂教学ppt课件

这是一份人教A版 (2019)选择性必修 第二册第五章 一元函数的导数及其应用5.3 导数在研究函数中的应用课堂教学ppt课件，共47页。PPT课件主要包含了自学导引，fx3，最大值和最小值，区间端点处，课堂互动，素养训练等内容，欢迎下载使用。

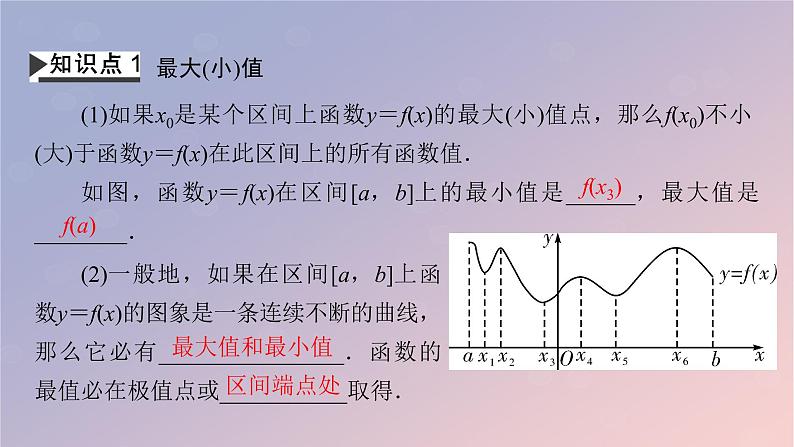
(1)如果x0是某个区间上函数y＝f(x)的最大(小)值点，那么f(x0)不小(大)于函数y＝f(x)在此区间上的所有函数值．如图，函数y＝f(x)在区间[a，b]上的最小值是______，最大值是________．
(2)一般地，如果在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，那么它必有________________．函数的最值必在极值点或___________取得．
【预习自测】1．函数的极值与最值的区别与联系？解：(1)极值是对某一点附近(局部)而言，最值是对函数的整个定义区间[a，b]而言；(2)在函数的定义区间[a，b]内，极大(小)值可能有多个(或者没有)，但最大(小)值只有一个；(3)函数f(x)的极值点不能是区间的端点，而最值点可以是区间的端点；(4)对于在闭区间上图象连续不断的函数，函数的最大(小)值必在极大(小)值点或区间端点处取得．
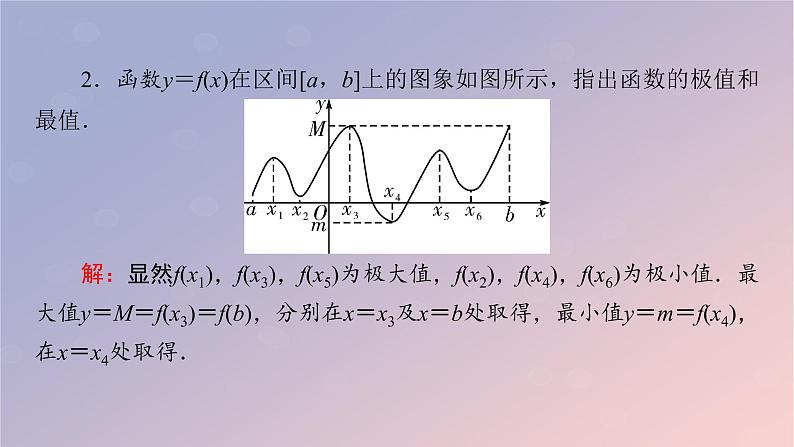
2．函数y＝f(x)在区间[a，b]上的图象如图所示，指出函数的极值和最值．解：显然f(x1)，f(x3)，f(x5)为极大值，f(x2)，f(x4)，f(x6)为极小值．最大值y＝M＝f(x3)＝f(b)，分别在x＝x3及x＝b处取得，最小值y＝m＝f(x4)，在x＝x4处取得．
(1)求函数y＝f(x)在(a，b)上的____________；(2)将函数y＝f(x)的各极值与_______________________比较，其中__________的一个是最大值，__________的一个是最小值．
求函数y＝f(x)在[a，b]上的最大值与最小值的步骤
端点处的函数值f(a)，f(b)
2．(2021年哈尔滨期末)函数f(x)＝x3－3x2＋m在区间[－1，1]上的最大值是2，则常数m＝(　　)A．－2B．0C．2D．4【答案】C【解析】f′(x)＝3x(x－2)，令f′(x)>0，解得x>2或x<0；令f′(x)<0，解得03．(2022年南通期末)函数y＝ln x－x在x∈(0，e]上的最大值为(　　)A．eB．1C．－eD．－1【答案】D
(2)f′(x)＝－4x3＋4x，由f′(x)＝－4x(x＋1)(x－1)＝0，得x＝－1或x＝0或x＝1，当x变化时，f′(x)，f(x)的变化情况如下表，
所以当x＝－3时，f(x)有最小值－60；当x＝－1或x＝1时，f(x)有最大值4.【解题探究】先求函数在(a，b)上的极值，然后与端点处函数值进行比较．
极值与最值是不一样的概念，在求闭区间上的最值时，切勿忘记端点的函数值．
题型2　利用最值求参数
解：f′(x)＝3x2－3ax＝3x(x－a)，由f′(x)＝0得x＝0或x＝a，当x变化时，f′(x)，f(x)的变化情况列表如下．
【解题探究】含有参数的函数最值求法与一般函数求法相同．
已知函数最值求参数的步骤(1)求出函数在给定区间上的极值及函数在区间端点处的函数值；(2)通过比较它们的大小，判断出哪个是最大值，哪个是最小值；(3)结合已知求出参数，进而使问题得以解决．
2．已知函数f(x)＝ax3－6ax2＋b在区间[－1，2]上的最大值是3，最小值是－29，求a，b的值．解：f′(x)＝3ax2－12ax＝3ax(x－4)，在区间[－1，2]上，令f′(x)＝0，得x＝0.由题知a≠0.当a＞0时，函数f(x)在x＝0处取得极大值，
又因为f(0)＝b，f(－1)＝－7a＋b，f(2)＝－16a＋b，故f(0)＞f(－1)＞f(2)，所以f(0)＝3，f(2)＝－29，解得a＝2，b＝3.当a＜0时，函数f(x)在x＝0处取得极小值且f(0)＜f(－1)＜f(2)，所以f(0)＝－29，f(2)＝3，解得a＝－2，b＝－29.
题型3　与最值有关的综合问题
∴f(x)∈[0，2e2]．又∵f(x)>m恒成立，∴f(x)min＞m，∴m<0.故m的取值范围为(－∞，0)．【解题探究】(1)解f′(x)＞0，f′(x)＜0即可；(2)首先求出f(x)在区间[－2，2]内的值域，再令f(x)min＞m即可．
在求解与最值有关的函数综合问题时，要发挥导数的解题功能，同时也要注意对字母的分类讨论；而有关恒成立问题，一般是转化为求函数的最值问题．
3．已知f(x)＝x3－x2－x＋3，x∈[－1，2]，f(x)－m<0恒成立，求实数m的取值范围．
题型4　用导数证明不等式
证明不等式f(x)＞g(x)，x∈(a，b)的步骤(1)将要证明的不等式f(x)＞g(x)移项可以转化为证明f(x)－g(x)＞0；(2)构造函数F(x)＝f(x)－g(x)，研究F(x)的单调性；(3)若[f(x)－g(x)]′＞0，说明函数F(x)＝f(x)－g(x)在(a，b)上单调递增，只需保证F(a)＞0；(4)若[f(x)－g(x)]′＜0，说明函数F(x)＝f(x)－g(x)在(a，b)上单调递减，只需保证F(b)＞0.
求函数f(x)＝4x3＋3x2－36x＋5在区间[－2，2]上的最大值和最小值．【错解】因为f(－2)＝57，f(2)＝－23，所以最大值为57，最小值为－23.【错因】一定注意不要只求区间端点处的函数值，这是较易出现错误的地方．
【警示】最值是指函数在自变量指定的取值范围内或隐含定义域内的最大值和最小值，要求出极值和区间端点处的函数值再比较．
1．函数的最值是一个整体性概念，最大值(最小值)必须是整个区间内所有函数值中的最大值(最小值)．函数在闭区间上若存在最大值或最小值，则最大值或最小值只能各有一个，具有唯一性；而极大值和极小值可能有多个，也可能没有．2．极值只能在函数区间的内部取得，而最值可以在区间的端点取得，有极值的不一定有最值，有最值的不一定有极值，极值有可能是最值，最值只要不在端点处则一定是极值．
3．如果函数f(x)在闭区间[a，b]上恰好单调，那么函数的最值恰好在两个端点处取到．当f(x)在闭区间[a，b]上单调递增时，f(a)是最小值，f(b)是最大值；当f(x)在闭区间[a，b]上单调递减时，f(a)是最大值，f(b)是最小值．
4．(题型2，4)(2021年北京期末)已知函数f(x)＝ex＋a－ax(a>0)的定义域为(1，＋∞)，若f(x)>0在(1，＋∞)上恒成立，则a的取值范围为__________．【答案】(0，e2)