数学选择性必修 第一册2.1 直线的倾斜角与斜率说课课件ppt

这是一份数学选择性必修 第一册2.1 直线的倾斜角与斜率说课课件ppt，共42页。PPT课件主要包含了k1＝k2，微思考，预习自测，k1·k2＝－1，l1⊥l2，答案D等内容，欢迎下载使用。

| 自 学 导 引 |
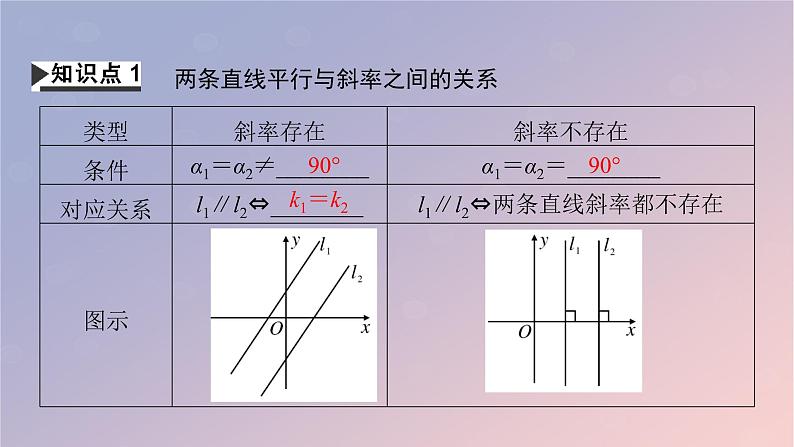
　　　　两条直线平行与斜率之间的关系
已知两条直线l1与l2平行，请根据两条直线平行的条件思考下列问题：(1)直线l1的倾斜角α1与直线l2的倾斜角α2有何关系？(2)这两条直线的斜率一定相等吗？【答案】(1)提示：直线l1，l2满足l1∥l2，即两条直线向上方向与x轴正向夹角相等，故直线l1，l2的倾斜角相等，即α1＝α2．(2)提示：不一定．只有在两条直线的斜率都存在的情况下，斜率才相等．
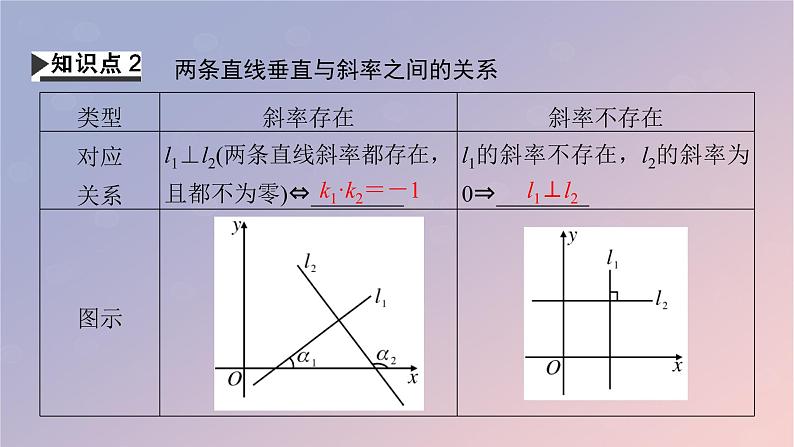
　　　　两条直线垂直与斜率之间的关系
【预习自测】若两条直线的斜率都不存在，那么这两条直线都与x轴(　　)A．垂直　B．重合　C．平行　D．位置不确定【答案】A　【解析】当两条直线的斜率都不存在时，这两条直线都垂直于x轴．
如果两条直线垂直，那么它们的斜率的积一定等于－1吗？【答案】提示：不一定．若两条直线的斜率都存在，它们垂直时斜率之积是－1，但若两条直线垂直时还可能它们的斜率一个是0，另一个不存在．
| 课 堂 互 动 |
提醒：若已知直线上点的坐标，判断直线是否平行时，要考虑直线重合的情况．
1．已知两平行直线的斜率是方程2x2－4x＋m－1＝0的两实数根，则m的值为(　　)A．1B．－1C．3D．－3【答案】C　【解析】由题意知方程2x2－4x＋m－1＝0的两实数根相等，所以Δ＝(－4)2－4×2×(m－1)＝0，解得m＝3．
2．直线l1的斜率为2，l1∥l2，直线l2过点(－1,1)且与y轴交于点P，则点P的坐标为(　　)A．(3,0)B．(－3,0)C．(0，－3)D．(0,3)【答案】D　
题型2　两条直线垂直的判定与应用　　　　(1)l1经过点A(3,2)，B(3，－1)，l2经过点M(1,1)，N(2,1)，判断l1与l2是否垂直；(2)已知直线l1经过点A(3，a)，B(a－2,3)，直线l2经过点C(2,3)，D(－1，a－2)，若l1⊥l2，求a的值．解：(1)直线l1的斜率不存在，直线l2的斜率为0，所以l1⊥l2．(2)由题意，知l2的斜率k2一定存在，l1的斜率可能不存在．当l1的斜率不存在时，3＝a－2，即a＝5，此时k2＝0，则l1⊥l2，满足题意．
使用斜率公式判定两直线垂直的步骤(1)一看：就是看所给两点的横坐标是否相等，若相等，则直线的斜率不存在，若不相等，则进行第二步．(2)二代：就是将点的坐标代入斜率公式．(3)三求值：计算斜率的值，进行判断．尤其是点的坐标中含有参数时，应用斜率公式对参数进行讨论．提醒：若已知点的坐标含有参数，利用两条直线的垂直关系求参数值时，要注意讨论斜率是否存在．
3．已知△ABC的顶点B(2,1)，C(－6,3)，其垂心为H(－3,2)，则其顶点A的坐标为________．【答案】(－19，－62)　
题型3　平行与垂直的综合应用　　　　如图，一个矩形花园里需要铺两条笔直的小路，已知矩形花园长AD＝5 m，宽AB＝3 m，其中一条小路定为AC，另一条小路过点D，问如何在BC上找到一点M，使得两条小路AC与DM相互垂直？
利用坐标法解决实际问题的三个步骤(1)建立恰当的平面直角坐标系．(2)将“形”转化为“数”进行运算．(3)将计算结果转化为实际问题所求解的问题．提醒：利用平行、垂直关系式的关键在于正确求解斜率，特别是含参数的问题，必须要分类讨论；其次要注意的是斜率不存在并不意味着问题无解．
4．(同类练)本例条件不变．若再在花园里设计一条过点M且与AC平行的小路，怎样设计？
5．(变式练)已知A(1，－1)，B(2,2)，C(3,0)三点，求点D，使直线CD⊥AB，且CB∥AD．
6．(拓展练)已知点A(0,3)，B(－1,0)，C(3,0)，求D点的坐标，使四边形ABCD为直角梯形(A，B，C，D按逆时针方向排列)．
解：设所求点D的坐标为(x，y)，如图，由于kAB＝3，kBC＝0，所以kAB·kBC＝0≠－1，即AB与BC不垂直．故AB，BC都不可作为直角梯形的直角腰．
规范解答　由两条直线平行、垂直的条件求参数的值　　　　已知直线l1经过点A(3，m)，B(m－1,2)，直线l2经过点C(1,2)，D(－2，m＋2)．(1)若l1∥l2，求m的值；(2)若l1⊥l2，求m的值．
【题后悟道】1．两条直线平行时关注是否重合由于斜率相等的两条直线可能平行，也可能重合，所以由两条直线平行得斜率相等，求参数的值后要注意检验，如本例中m＝1或m＝6时，经检验l1与l2不重合．
| 素 养 达 成 |
1．对两条直线平行的判定条件的理解l1∥l2⇔k1＝k2成立的前提条件有两个：①两条直线的斜率都存在；②这两条直线不重合．
2．两条直线垂直的判定必须注意的三个问题(1)利用l1⊥l2⇔k1·k2＝－1判断两条直线垂直的前提是这两条直线的斜率都存在，且都不为0．(2)若k1·k2≠－1，则两条直线一定不会垂直．(3)若两条直线中，一条直线斜率不存在，同时另一条直线的斜率等于零，则两条直线垂直．这样，两条直线垂直的判定的条件就可叙述为：l1⊥l2⇔k1·k2＝－1或一条直线斜率不存在，同时另一条直线的斜率等于零．
1．(题型1)过点A(2,5)和点B(－4,5)的直线与直线y＝3的位置关系是(　　)A．相交B．平行C．重合D．以上都不对【答案】B　【解析】由斜率公式计算得，过点A(2,5)和点B(－4,5)的直线的斜率为0，且直线AB不与y＝3重合．
3．(题型2)直线l1，l2满足l1⊥l2，若直线l1的倾斜角为30°，则直线l2的斜率为________．
4．(题型2)l1过点A(m,1)，B(－3,4)，l2过点C(0,2)，D(1,1)，且l1∥l2，则m＝________．【答案】0　
5．(题型3)已知直线l的倾斜角为30°，点P(2,1)在直线l上，直线l绕点P(2,1)按逆时针方向旋转30°后到达直线l1的位置，此时直线l1与l2平行，且l2是线段AB的垂直平分线，其中A(1，m－1)，B(m,2)，试求实数m的值．