

江西省高安二中2022年中考数学仿真试卷含解析
展开
这是一份江西省高安二中2022年中考数学仿真试卷含解析,共17页。试卷主要包含了计算3÷2的结果是等内容,欢迎下载使用。
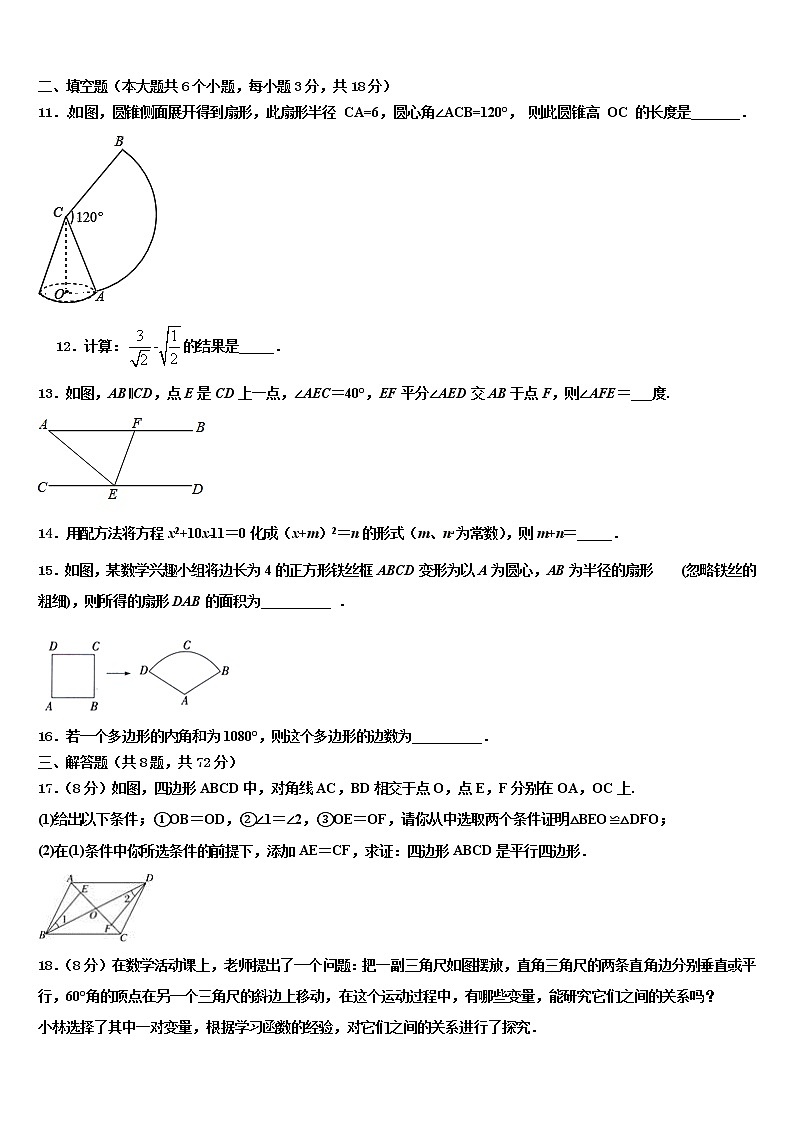
2021-2022中考数学模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(共10小题,每小题3分,共30分)1.如果与互补,与互余,则与的关系是( )A. B.C. D.以上都不对2.如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )A. B.C. D.3.有一圆形苗圃如图1所示,中间有两条交叉过道AB,CD,它们为苗圃的直径,且AB⊥CD.入口K 位于中点,园丁在苗圃圆周或两条交叉过道上匀速行进.设该园丁行进的时间为x,与入口K的距离为y,表示y与x的函数关系的图象大致如图2所示,则该园丁行进的路线可能是( )A.A→O→D B.C→A→O→ B C.D→O→C D.O→D→B→C4.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )A.五丈 B.四丈五尺 C.一丈 D.五尺5.如图,在△ABC中,EF∥BC,,S四边形BCFE=8,则S△ABC=( )A.9 B.10 C.12 D.136.人的大脑每天能记录大约8 600万条信息,数据8 600用科学记数法表示为( )A.0.86×104 B.8.6×102 C.8.6×103 D.86×1027.已知a+b=4,c﹣d=﹣3,则(b+c)﹣(d﹣a)的值为( )A.7 B.﹣7 C.1 D.﹣18.计算(-ab2)3÷(-ab)2的结果是( )A.ab4 B.-ab4 C.ab3 D.-ab39.如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形,转动这个四边形,使它形状改变,当,时,等于( )A. B. C. D.10.如图,AB为⊙O的直径,C、D为⊙O上的点,若AC=CD=DB,则cos∠CAD =( )A. B. C. D.二、填空题(本大题共6个小题,每小题3分,共18分)11..如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°, 则此圆锥高 OC 的长度是_______.12.计算:的结果是_____.13.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE=___度.14.用配方法将方程x2+10x﹣11=0化成(x+m)2=n的形式(m、n为常数),则m+n=_____.15.如图,某数学兴趣小组将边长为4的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形 (忽略铁丝的粗细),则所得的扇形DAB的面积为__________ .16.若一个多边形的内角和为1080°,则这个多边形的边数为__________.三、解答题(共8题,共72分)17.(8分)如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上.(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.18.(8分)在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.下面是小林的探究过程,请补充完整:(1)画出几何图形,明确条件和探究对象;如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.(2)通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm0123456y/cm6.95.34.03.3 4.56(说明:补全表格时相关数据保留一位小数)(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.19.(8分)我们知道中,如果,,那么当时,的面积最大为6;(1)若四边形中,,且,直接写出满足什么位置关系时四边形面积最大?并直接写出最大面积.(2)已知四边形中,,求为多少时,四边形面积最大?并求出最大面积是多少?20.(8分)如图,水渠边有一棵大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°.求C处到树干DO的距离CO.(结果精确到1米)(参考数据:,)21.(8分)问题提出(1).如图 1,在四边形 ABCD 中,AB=BC,AD=CD=3, ∠BAD=∠BCD=90°,∠ADC=60°,则四边形 ABCD 的面积为 _;问题探究(2).如图 2,在四边形 ABCD 中,∠BAD=∠BCD=90°,∠ABC=135°,AB=2 2,BC=3,在 AD、CD 上分别找一点 E、F, 使得△BEF 的周长最小,作出图像即可. 22.(10分) “大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:请根据图中提供的信息,解答下列问题:(1)求被调查的学生总人数;(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.23.(12分)某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.24.计算:2cos30°+--()-2
参考答案 一、选择题(共10小题,每小题3分,共30分)1、C【解析】
根据∠1与∠2互补,∠2与∠1互余,先把∠1、∠1都用∠2来表示,再进行运算.【详解】∵∠1+∠2=180°∴∠1=180°-∠2又∵∠2+∠1=90°∴∠1=90°-∠2∴∠1-∠1=90°,即∠1=90°+∠1.故选C.【点睛】此题主要记住互为余角的两个角的和为90°,互为补角的两个角的和为180度.2、A【解析】
由图形可以知道,由大正方形的面积-小正方形的面积=矩形的面积,进而可以证明平方差公式.【详解】解:大正方形的面积-小正方形的面积=,
矩形的面积=,
故,
故选:A.【点睛】本题主要考查平方差公式的几何意义,用两种方法表示阴影部分的面积是解题的关键.3、B【解析】【分析】观察图象可知园丁与入口K的距离先减小,然后再增大,但是没有到过入口的位置,据此逐项进行分析即可得.【详解】A. A→O→D,园丁与入口的距离逐渐增大,逐渐减小,不符合;B. C→A→O→ B,园丁与入口的距离逐渐减小,然后又逐渐增大,符合;C. D→O→C,园丁与入口的距离逐渐增大,不符合;D. O→D→B→C,园丁与入口的距离先逐渐变小,然后再逐渐变大,再逐渐变小,不符合,故选B.【点睛】本题考查了动点问题的函数图象,看懂图形,认真分析是解题的关键.4、B【解析】【分析】根据同一时刻物高与影长成正比可得出结论.【详解】设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴,解得x=45(尺),故选B.【点睛】本题考查了相似三角形的应用举例,熟知同一时刻物髙与影长成正比是解答此题的关键.5、A【解析】
由在△ABC中,EF∥BC,即可判定△AEF∽△ABC,然后由相似三角形面积比等于相似比的平方,即可求得答案.【详解】∵,∴.又∵EF∥BC,∴△AEF∽△ABC.∴.∴1S△AEF=S△ABC.又∵S四边形BCFE=8,∴1(S△ABC﹣8)=S△ABC,解得:S△ABC=1.故选A.6、C【解析】
科学记数法就是将一个数字表示成a×10的n次幂的形式,其中1≤|a|<10,n表示整数.n为整数位数减1,即从左边第一位开始,在首位非零的后面加上小数点,再乘以10的n次幂.【详解】数据8 600用科学记数法表示为8.6×103故选C.【点睛】用科学记数法表示一个数的方法是(1)确定a:a是只有一位整数的数;(2)确定n:当原数的绝对值≥10时,n为正整数,n等于原数的整数位数减1;当原数的绝对值<1时,n为负整数,n的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零).7、C【解析】试题分析:原式去括号可得b-c+d+a=(a+b)-(c-d)=4-(-3)=1.故选A.考点:代数式的求值;整体思想.8、B【解析】根据积的乘方的运算法则,先分别计算积的乘方,然后再根据单项式除法法则进行计算即可得,(-ab2)3÷(-ab)2=-a3b6÷a2b2=-ab4,故选B.9、B【解析】
首先连接AC,由将四根长度相等的细木条首尾相连,用钉子钉成四边形ABCD,AB=1,,易得△ABC是等边三角形,即可得到答案.【详解】连接AC,
∵将四根长度相等的细木条首尾相连,用钉子钉成四边形ABCD,
∴AB=BC,
∵,
∴△ABC是等边三角形,
∴AC=AB=1.
故选:B.【点睛】本题考点:菱形的性质.10、D【解析】
根据圆心角,弧,弦的关系定理可以得出===,根据圆心角和圆周角的关键即可求出的度数,进而求出它的余弦值.【详解】解:===,故选D.【点睛】本题考查圆心角,弧,弦,圆周角的关系,熟记特殊角的三角函数值是解题的关键. 二、填空题(本大题共6个小题,每小题3分,共18分)11、4【解析】
先根据圆锥的侧面展开图,扇形的弧长等于该圆锥的底面圆的周长,求出 OA,最后用勾股定理即可得出结论.【详解】设圆锥底面圆的半径为 r,∵AC=6,∠ACB=120°,∴=2πr, ∴r=2,即:OA=2,在 Rt△AOC 中,OA=2,AC=6,根据勾股定理得,OC==4, 故答案为4.【点睛】本题考查了扇形的弧长公式,圆锥的侧面展开图,勾股定理,求出 OA的长是解本题的关键.12、【解析】试题分析:先进行二次根式的化简,然后合并同类二次根式即可,考点:二次根式的加减13、70°.【解析】
由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.【详解】∵∠AEC=40°,∴∠AED=180°﹣∠AEC=140°,∵EF平分∠AED,∴,又∵AB∥CD,∴∠AFE=∠DEF=70°.故答案为:70【点睛】本题考查的是平行线的性质以及角平分线的定义.熟练掌握平行线的性质,求出∠DEF的度数是解决问题的关键.14、1【解析】
方程常数项移到右边,两边加上25配方得到结果,求出m与n的值即可.【详解】解:∵x2+10x-11=0,∴x2+10x=11,则x2+10x+25=11+25,即(x+5)2=36,∴m=5、n=36,∴m+n=1,故答案为1.【点睛】此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.15、【解析】
设扇形的圆心角为n°,则根据扇形的弧长公式有: ,解得 所以16、1【解析】
根据多边形内角和定理:(n﹣2)•110 (n≥3)可得方程110(x﹣2)=1010,再解方程即可.【详解】解:设多边形边数有x条,由题意得:110(x﹣2)=1010,解得:x=1,故答案为:1.【点睛】此题主要考查了多边形内角和定理,关键是熟练掌握计算公式:(n﹣2)•110 (n≥3). 三、解答题(共8题,共72分)17、(1)见解析;(2)见解析.【解析】试题分析:(1)选取①②,利用ASA判定△BEO≌△DFO;也可选取②③,利用AAS判定△BEO≌△DFO;还可选取①③,利用SAS判定△BEO≌△DFO;(2)根据△BEO≌△DFO可得EO=FO,BO=DO,再根据等式的性质可得AO=CO,根据两条对角线互相平分的四边形是平行四边形可得结论.试题解析:证明:(1)选取①②,∵在△BEO和△DFO中,∴△BEO≌△DFO(ASA);(2)由(1)得:△BEO≌△DFO,∴EO=FO,BO=DO,∵AE=CF,∴AO=CO,∴四边形ABCD是平行四边形.点睛:此题主要考查了平行四边形的判定,以及全等三角形的判定,关键是掌握两条对角线互相平分的四边形是平行四边形.18、(1)见解析;(1)3.5;(3)见解析; (4)3.1【解析】
根据题意作图测量即可.【详解】(1)取点、画图、测量,得到数据为3.5故答案为:3.5(3)由数据得(4)当△DEF为等边三角形是,EF=DE,由∠B=45°,射线DE⊥BC于点E,则BE=EF.即y=x所以,当(1)中图象与直线y=x相交时,交点横坐标即为BE的长,由作图、测量可知x约为3.1.【点睛】本题为动点问题的函数图象探究题,解得关键是按照题意画图测量,并将条件转化成函数图象研究.19、 (1)当,时有最大值1;(2)当时,面积有最大值32.【解析】
(1)由题意当AD∥BC,BD⊥AD时,四边形ABCD的面积最大,由此即可解决问题.
(2)设BD=x,由题意:当AD∥BC,BD⊥AD时,四边形ABCD的面积最大,构建二次函数,利用二次函数的性质即可解决问题.【详解】(1) 由题意当AD∥BC,BD⊥AD时,四边形ABCD的面积最大,
最大面积为×6×(16-6)=1.故当,时有最大值1;(2)当,时有最大值,设, 由题意:当AD∥BC,BD⊥AD时,四边形ABCD的面积最大,∴抛物线开口向下∴当 时,面积有最大值32.【点睛】本题考查三角形的面积,二次函数的应用等知识,解题的关键是学会利用参数构建二次函数解决问题.20、解:设OC=x,在Rt△AOC中,∵∠ACO=45°,∴OA=OC=x.在Rt△BOC中,∵∠BCO=30°,∴.∵AB=OA﹣OB=,解得.∴OC=5米.答:C处到树干DO的距离CO为5米.【解析】解直角三角形的应用(仰角俯角问题),锐角三角函数定义,特殊角的三角函数值.【分析】设OC=x,在Rt△AOC中,由于∠ACO=45°,故OA=x,在Rt△BOC中,由于∠BCO=30°,故,再根据AB=OA-OB=2即可得出结论.21、(1)3 ,(2)见解析【解析】
(1)易证△ABD≌△CBD,再利用含30°的直角三角形求出AB、BD的长,即可求出面积.(2)作点B关于AD的对称点B’,点B关于CD的对应点B’’,连接B’B’’,与AD、CD交于EF,△AEF即为所求.【详解】(1)∵AB=BC,AD=CD=3, ∠BAD=∠BCD=90°,∴△ABD≌△CBD(HL)∴∠ADB=∠CDB=∠ADC=30°,∴AB=∴S△ABD==∴四边形ABCD的面积为2S△ABD=(2)作点B关于AD的对称点B’,点B关于CD的对应点B’’,连接B’B’’,与AD、CD交于EF,△BEF的周长为BE+EF+BF=B’E+EF+B’’F=B’B’’为最短.故此时△BEF的周长最小.【点睛】此题主要考查含30°的直角三角形与对称性的应用,解题的关键是根据题意作出相应的图形进行求解.22、(1)40;(2)72;(3)1.【解析】
(1)用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数;(2)先计算出最想去D景点的人数,再补全条形统计图,然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数;(3)用800乘以样本中最想去A景点的人数所占的百分比即可.【详解】(1)被调查的学生总人数为8÷20%=40(人);(2)最想去D景点的人数为40﹣8﹣14﹣4﹣6=8(人),补全条形统计图为:扇形统计图中表示“最想去景点D”的扇形圆心角的度数为×360°=72°;(3)800×=1,所以估计“最想去景点B“的学生人数为1人.23、(1)不可能;(2).【解析】
(1)利用确定事件和随机事件的定义进行判断;(2)画树状图展示所有12种等可能的结果数,再找出其中某顾客该天早餐刚好得到菜包和油条的结果数,然后根据概率公式计算.【详解】(1)某顾客在该天早餐得到两个鸡蛋”是不可能事件;故答案为不可能;(2)画树状图:共有12种等可能的结果数,其中某顾客该天早餐刚好得到菜包和油条的结果数为2,所以某顾客该天早餐刚好得到菜包和油条的概率=.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.24、5【解析】
根据实数的计算,先把各数化简,再进行合并即可.【详解】原式==5【点睛】此题主要考查实数的计算,解题的关键是熟知特殊三角函数的化简与二次根式的运算.
相关试卷
这是一份2023年江西省宜春市高安市中考数学二模试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份江西省宜春市高安市高安中学2022年中考数学五模试卷含解析,共24页。试卷主要包含了一、单选题等内容,欢迎下载使用。
这是一份2022年江西省高安中学中考考前最后一卷数学试卷含解析,共27页。试卷主要包含了的值是,如图,已知直线l1等内容,欢迎下载使用。









