江西省高安市重点名校2022年中考四模数学试题含解析

这是一份江西省高安市重点名校2022年中考四模数学试题含解析，共22页。试卷主要包含了运用乘法公式计算等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．估计-1的值在（ ）
A．0到1之间 B．1到2之间 C．2到3之间 D．3至4之间
2．下列调查中，最适合采用普查方式的是（　　）
A．对太原市民知晓“中国梦”内涵情况的调查
B．对全班同学1分钟仰卧起坐成绩的调查
C．对2018年央视春节联欢晚会收视率的调查
D．对2017年全国快递包裹产生的包装垃圾数量的调查
3．如图是某个几何体的展开图，该几何体是（ ）

A．三棱柱 B．圆锥 C．四棱柱 D．圆柱
4．如图，要使□ABCD成为矩形，需添加的条件是（）

A．AB=BC B．∠ABC=90° C．AC⊥BD D．∠1=∠2
5．运用乘法公式计算（4+x）（4﹣x）的结果是（　　）
A．x2﹣16 B．16﹣x2 C．16﹣8x+x2 D．8﹣x2
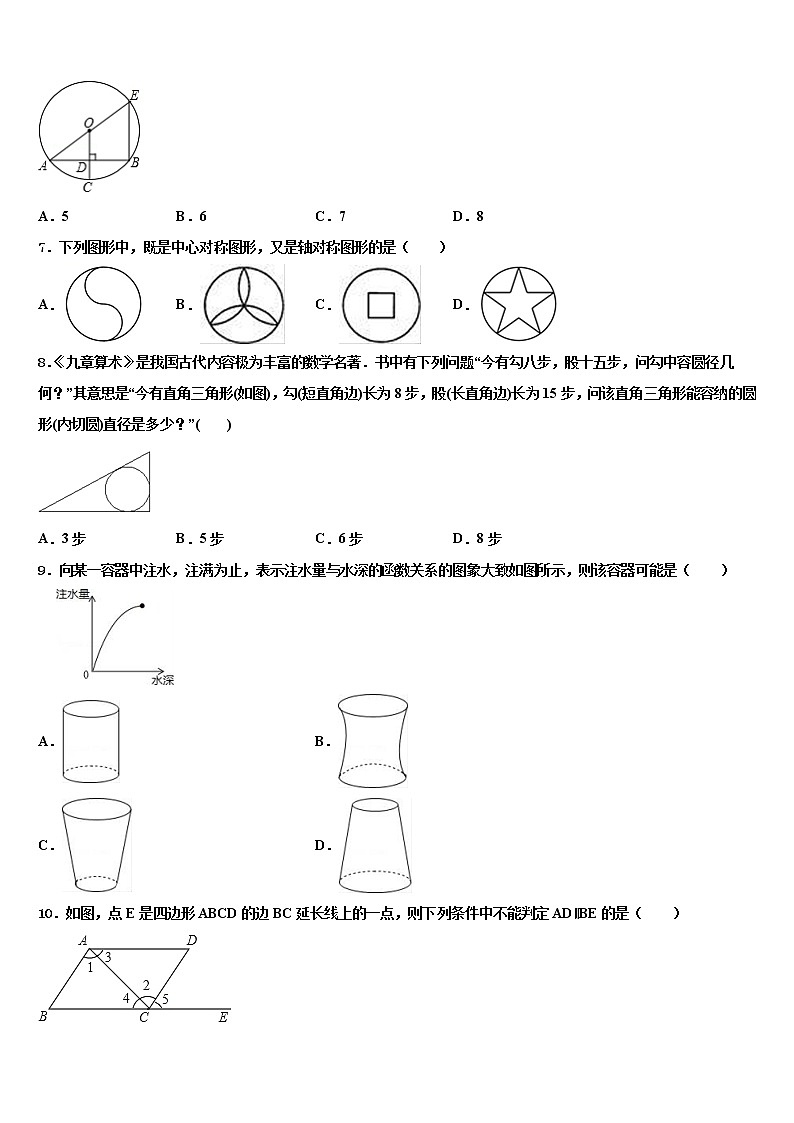
6．如图，在⊙O中，AE是直径，半径OC垂直于弦AB于D，连接BE，若AB=2，CD=1，则BE的长是　　

A．5 B．6 C．7 D．8
7．下列图形中，既是中心对称图形，又是轴对称图形的是（ ）
A． B． C． D．
8．《九章算术》是我国古代内容极为丰富的数学名著．书中有下列问题“今有勾八步，股十五步，问勾中容圆径几何？”其意思是“今有直角三角形(如图)，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形能容纳的圆形(内切圆)直径是多少？”(　　)

A．3步 B．5步 C．6步 D．8步
9．向某一容器中注水，注满为止，表示注水量与水深的函数关系的图象大致如图所示，则该容器可能是（　　）

A． B．
C． D．
10．如图，点E是四边形ABCD的边BC延长线上的一点，则下列条件中不能判定AD∥BE的是（　　）

A． B． C． D．
11．据相关报道，开展精准扶贫工作五年以来，我国约有55000000人摆脱贫困，将55000000用科学记数法表示是（ ）
A．55×106 B．0.55×108 C．5.5×106 D．5.5×107
12．下面计算中，正确的是（　　）
A．（a+b）2=a2+b2 B．3a+4a=7a2
C．（ab）3=ab3 D．a2•a5=a7
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如图，在矩形ABCD中，DE⊥AC，垂足为E，且tan∠ADE＝，AC＝5，则AB的长____．

14．如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，则大厅两层之间的高度为____米．（结果保留两个有效数字）（参考数据；sin31°=0.515，cos31°=0.857，tan31°=0.601）

15．如图，菱形ABCD中，AB=4，∠C=60°，菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过6次这样的操作菱形中心（对角线的交点）O所经过的路径总长为_____．

16．如果点、是二次函数是常数图象上的两点，那么______填“”、“”或“”
17．如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y=的图象上，则k的值为________.

18．如图，△ABC与△DEF位似，点O为位似中心，若AC＝3DF，则OE：EB＝_____．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）如图，有四张背面相同的卡片A、B、C、D，卡片的正面分别印有正三角形、平行四边形、圆、正五边形（这些卡片除图案不同外，其余均相同）．把这四张卡片背面向上洗匀后，进行下列操作：若任意抽取其中一张卡片，抽到的卡片既是中心对称图形又是轴对称图形的概率是　 　；若任意抽出一张不放回，然后再从余下的抽出一张．请用树状图或列表表示摸出的两张卡片所有可能的结果，求抽出的两张卡片的图形是中心对称图形的概率．

20．（6分）如图，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），B（4，0）与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线1，交抛物线与点Q．求抛物线的解析式；当点P在线段OB上运动时，直线1交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；在点P运动的过程中，坐标平面内是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

21．（6分）如图1，AB为半圆O的直径，半径的长为4cm，点C为半圆上一动点，过点C作CE⊥AB，垂足为点E，点D为弧AC的中点，连接DE，如果DE=2OE，求线段AE的长．
小何根据学习函数的经验，将此问题转化为函数问题解决．
小华假设AE的长度为xcm，线段DE的长度为ycm．
（当点C与点A重合时，AE的长度为0cm），对函数y随自变量x的变化而变化的规律进行探究．
下面是小何的探究过程，请补充完整：（说明：相关数据保留一位小数）．
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm
0
1
2
3
4
5
6
7
8
y/cm
0
1.6
2.5
3.3
4.0
4.7
　 　
5.8
5.7
当x=6cm时，请你在图中帮助小何完成作图，并使用刻度尺度量此时线段DE的长度，填写在表格空白处：
（2）在图2中建立平面直角坐标系，描出补全后的表中各组对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象解决问题，当DE=2OE时，AE的长度约为　 　cm．

22．（8分）如图，在Rt△ABC中，∠C＝90°，AC，tanB，半径为2的⊙C分别交AC，BC于点D、E，得到DE弧．求证：AB为⊙C的切线．求图中阴影部分的面积．

23．（8分）先化简，再求值：（m+2﹣）•，其中m=﹣．
24．（10分）如图，以AD为直径的⊙O交AB于C点，BD的延长线交⊙O于E点，连CE交AD于F点，若AC＝BC．
（1）求证：；
（2）若，求tan∠CED的值．

25．（10分）如图，AB∥CD，E、F分别为AB、CD上的点，且EC∥BF，连接AD，分别与EC、BF相交与点G、H，若AB＝CD，求证：AG＝DH．

26．（12分）如图，在规格为8×8的边长为1个单位的正方形网格中（每个小正方形的边长为1），△ABC的三个顶点都在格点上，且直线m、n互相垂直．
（1）画出△ABC关于直线n的对称图形△A′B′C′；
（2）直线m上存在一点P，使△APB的周长最小；
①在直线m上作出该点P；（保留画图痕迹）
②△APB的周长的最小值为　 　．（直接写出结果）

27．（12分）“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
请结合图表完成下列各题：
（1）①表中a的值为 ，中位数在第 组；
②频数分布直方图补充完整；
（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．
组别
成绩x分
频数（人数）
第1组
50≤x＜60
6
第2组
60≤x＜70
8
第3组
70≤x＜80
14
第4组
80≤x＜90
a
第5组
90≤x＜100
10




参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
试题分析：∵2＜＜3，
∴1＜-1＜2，
即-1在1到2之间，
故选B．
考点：估算无理数的大小．
2、B
【解析】分析：由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
详解：A、调查范围广适合抽样调查，故A不符合题意；
B、适合普查，故B符合题意；
C、调查范围广适合抽样调查，故C不符合题意；
D、调查范围广适合抽样调查，故D不符合题意；
故选：B．
点睛：本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
3、A
【解析】
侧面为三个长方形，底边为三角形，故原几何体为三棱柱．
【详解】
解：观察图形可知，这个几何体是三棱柱．
故选A．
【点睛】
本题考查的是三棱柱的展开图，对三棱柱有充分的理解是解题的关键．．
4、B
【解析】
根据一个角是90度的平行四边形是矩形进行选择即可．
【详解】
解：A、是邻边相等，可判定平行四边形ABCD是菱形；
B、是一内角等于90°，可判断平行四边形ABCD成为矩形；
C、是对角线互相垂直，可判定平行四边形ABCD是菱形；
D、是对角线平分对角，可判断平行四边形ABCD成为菱形；
故选：B．
【点睛】
本题主要应用的知识点为：矩形的判定． ①对角线相等且相互平分的四边形为矩形．②一个角是90度的平行四边形是矩形．
5、B
【解析】
根据平方差公式计算即可得解．
【详解】
，
故选：B．
【点睛】
本题主要考查了整式的乘法公式，熟练掌握平方差公式的运算是解决本题的关键.
6、B
【解析】
根据垂径定理求出AD,根据勾股定理列式求出半径 ，根据三角形中位线定理计算即可．
【详解】
解：∵半径OC垂直于弦AB，
∴AD=DB= AB=
在Rt△AOD中，OA2=(OC-CD)2+AD2,即OA2=(OA-1)2+( )2，
解得，OA=4
∴OD=OC-CD=3，
∵AO=OE,AD=DB,
∴BE=2OD=6
故选B
【点睛】
本题考查的是垂径定理、勾股定理，掌握垂直于弦的直径平分这条弦是解题的关键
7、C
【解析】
根据中心对称图形和轴对称图形对各选项分析判断即可得解．
【详解】
A、不是轴对称图形，是中心对称图形，故本选项错误；
B、不是中心对称图形，是轴对称图形，故本选项错误；
C、既是中心对称图形，又是轴对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选C．
【点睛】
本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
8、C
【解析】
试题解析：根据勾股定理得：斜边为
则该直角三角形能容纳的圆形(内切圆)半径 (步)，即直径为6步，
故选C
9、D
【解析】
根据函数的图象和所给出的图形分别对每一项进行判断即可.
【详解】
由函数图象知: 随高度h的增加, y也增加,但随h变大, 每单位高度的增加, 注水量h的增加量变小, 图象上升趋势变缓, 其原因只能是水瓶平行于底面的截面的半径由底到顶逐渐变小, 故D项正确.
故选: D.
【点睛】
本题主要考查函数模型及其应用.
10、A
【解析】
利用平行线的判定方法判断即可得到结果．
【详解】
∵∠1=∠2，
∴AB∥CD，选项A符合题意；
∵∠3=∠4，
∴AD∥BC，选项B不合题意；
∵∠D=∠5，
∴AD∥BC，选项C不合题意；
∵∠B+∠BAD=180°，
∴AD∥BC，选项D不合题意，
故选A．
【点睛】
此题考查了平行线的判定，熟练掌握平行线的判定方法是解本题的关键．
11、D
【解析】
试题解析：55000000=5.5×107，
故选D．
考点：科学记数法—表示较大的数
12、D
【解析】
直接利用完全平方公式以及合并同类项法则、积的乘方运算法则分别化简得出答案．
【详解】
A. (a+b)2=a2+b2+2ab，故此选项错误；
B. 3a+4a=7a，故此选项错误；
C. (ab)3=a3b3，故此选项错误；
D. a2×a5=a7，正确。
故选：D.
【点睛】
本题考查了幂的乘方与积的乘方，合并同类项，同底数幂的乘法，完全平方公式，解题的关键是掌握它们的概念进行求解.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、3.
【解析】
先根据同角的余角相等证明∠ADE＝∠ACD，在△ADC根据锐角三角函数表示用含有k的代数式表示出AD=4k和DC=3k，从而根据勾股定理得出AC=5k，又AC=5，从而求出DC的值即为AB.
【详解】
∵四边形ABCD是矩形，
∴∠ADC＝90°，AB＝CD，
∵DE⊥AC，
∴∠AED＝90°，
∴∠ADE+∠DAE＝90°，∠DAE+∠ACD＝90°，
∴∠ADE＝∠ACD，
∴tan∠ACD＝tan∠ADE＝＝，
设AD＝4k，CD＝3k，则AC＝5k，
∴5k＝5，
∴k＝1，
∴CD＝AB＝3，
故答案为3.
【点睛】
本题考查矩形的性质和利用锐角三角函数解直角三角形，解决此类问题时需要将已知角的三角函数、已知边、未知边，转换到同一直角三角形中，然后解决问题.
14、6.2
【解析】
根据题意和锐角三角函数可以求得BC的长，从而可以解答本题.
【详解】
解：在Rt△ABC中，
∵∠ACB=90°，
∴BC=AB•sin∠BAC=12×0.515≈6.2（米），
答：大厅两层之间的距离BC的长约为6.2米．
故答案为：6.2.
【点睛】
本题考查解直角三角形的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用锐角三角函数和数形结合的思想解答.
15、
【解析】
第一次旋转是以点A为圆心，那么菱形中心旋转的半径就是OA，解直角三角形可求出OA的长，圆心角是60°．第二次还是以点A为圆心，那么菱形中心旋转的半径就是OA，圆心角是60°．第三次就是以点B为旋转中心，OB为半径，旋转的圆心角为60度．旋转到此菱形就又回到了原图．故这样旋转6次，就是2个这样的弧长的总长，进而得出经过6次这样的操作菱形中心O所经过的路径总长．
【详解】
解：∵菱形ABCD中，AB=4，∠C=60°，
∴△ABD是等边三角形， BO=DO=2，
AO==,
第一次旋转的弧长=，
∵第一、二次旋转的弧长和=+=，
第三次旋转的弧长为：，
故经过6次这样的操作菱形中心O所经过的路径总长为：2×（+）=．
故答案为：．

【点睛】
本题考查菱形的性质，翻转的性质以及解直角三角形的知识．
16、
【解析】
根据二次函数解析式可知函数图象对称轴是x=0，且开口向上，分析可知两点均在对称轴左侧的图象上；接下来，结合二次函数的性质可判断对称轴左侧图象的增减性，
【详解】
解：二次函数的函数图象对称轴是x=0，且开口向上，
∴在对称轴的左侧y随x的增大而减小，
∵-3＞-4，∴＞.
故答案为＞.
【点睛】
本题考查了二次函数的图像和数形结合的数学思想.
17、-6
【解析】
因为四边形OABC是菱形,所以对角线互相垂直平分,则点A和点C关于y轴对称,点C在反比例函数上,设点C的坐标为(x,),则点A的坐标为(－x,),点B的坐标为(0,),因此AC=－2x,OB=,根据菱形的面积等于对角线乘积的一半得:
,解得
18、1:2
【解析】
△ABC与△DEF是位似三角形，则DF∥AC，EF∥BC，先证明△OAC∽△ODF，利用相似比求得AC＝3DF，所以可求OE：OB＝DF：AC＝1：3，据此可得答案．
【详解】
解：∵△ABC与△DEF是位似三角形，
∴DF∥AC，EF∥BC
∴△OAC∽△ODF，OE：OB＝OF：OC
∴OF：OC＝DF：AC
∵AC＝3DF
∴OE：OB＝DF：AC＝1：3，
则OE：EB＝1：2
故答案为：1：2
【点睛】
本题考查了位似的相关知识，位似是相似的特殊形式，位似比等于相似比，位似图形的对应顶点的连线平行或共线．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）；（2）.
【解析】
（1）既是中心对称图形又是轴对称图形只有圆一个图形，然后根据概率的意义解答即可；
（2）画出树状图，然后根据概率公式列式计算即可得解．
【详解】
（1）∵正三角形、平行四边形、圆、正五边形中只有圆既是中心对称图形又是轴对称图形，
∴抽到的卡片既是中心对称图形又是轴对称图形的概率是；
（2）根据题意画出树状图如下：

一共有12种情况，抽出的两张卡片的图形是中心对称图形的是B、C共有2种情况，
所以，P（抽出的两张卡片的图形是中心对称图形）．
【点睛】
本题考查了列表法和树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
20、 (1) ;(2) 当m＝2时，四边形CQMD为平行四边形;(3) Q1（8，18）、Q2（﹣1，0）、Q3（3，﹣2）
【解析】
（1）直接将A（-1，0），B（4，0）代入抛物线y=x2+bx+c方程即可；
（2）由（1）中的解析式得出点C的坐标C（0，-2），从而得出点D（0，2），求出直线BD：y＝−x+2，设点M(m，−m+2)，Q(m，m2−m−2)，可得MQ=−m2+m+4，根据平行四边形的性质可得QM=CD=4，即−m2+m+4＝4可解得m=2；
（3）由Q是以BD为直角边的直角三角形，所以分两种情况讨论，①当∠BDQ=90°时，则BD2+DQ2=BQ2，列出方程可以求出Q1（8，18），Q2（-1，0），②当∠DBQ=90°时，则BD2+BQ2=DQ2，列出方程可以求出Q3（3，-2）．
【详解】
（1）由题意知，
∵点A（﹣1，0），B（4，0）在抛物线y＝x2+bx+c上，
∴解得：
∴所求抛物线的解析式为
（2）由（1）知抛物线的解析式为，令x＝0，得y＝﹣2
∴点C的坐标为C（0，﹣2）
∵点D与点C关于x轴对称
∴点D的坐标为D（0，2）
设直线BD的解析式为：y＝kx+2且B（4，0）
∴0＝4k+2，解得：
∴直线BD的解析式为：
∵点P的坐标为（m，0），过点P作x轴的垂线1，交BD于点M，交抛物线与点Q
∴可设点M，Q
∴MQ＝
∵四边形CQMD是平行四边形
∴QM＝CD＝4，即=4
解得：m1＝2，m2＝0（舍去）
∴当m＝2时，四边形CQMD为平行四边形
（3）由题意，可设点Q且B（4，0）、D（0，2）
∴BQ2＝
DQ2＝
BD2＝20
①当∠BDQ＝90°时，则BD2+DQ2＝BQ2，
∴
解得：m1＝8，m2＝﹣1，此时Q1（8，18），Q2（﹣1，0）
②当∠DBQ＝90°时，则BD2+BQ2＝DQ2，
∴
解得：m3＝3，m4＝4，（舍去）此时Q3（3，﹣2）
∴满足条件的点Q的坐标有三个，分别为：Q1（8，18）、Q2（﹣1，0）、Q3（3，﹣2）．
【点睛】
此题考查了待定系数法求解析式，还考查了平行四边形及直角三角形的定义，要注意第3问分两种情形求解．
21、（1）5.3（2）见解析（3）2.5或6.9
【解析】
（1）（2）按照题意取点、画图、测量即可．（3）中需要将DE=2OE转换为y与x的函数关系，注意DE为非负数，函数为分段函数．
【详解】
（1）根据题意取点、画图、测量的x=6时，y=5.3
故答案为5.3
（2）根据数据表格画图象得

（3）当DE=2OE时，问题可以转化为折线y= 与（2）中图象的交点
经测量得x=2.5或6.9时DE=2OE．
故答案为2.5或6.9
【点睛】
动点问题的函数图象探究题，考查了函数图象的画法，应用了数形结合思想和转化的数学思想．
22、 (1)证明见解析；(2)1-π.
【解析】
（1）解直角三角形求出BC，根据勾股定理求出AB，根据三角形面积公式求出CF，根据切线的判定得出即可；
（2）分别求出△ACB的面积和扇形DCE的面积，即可得出答案．
【详解】
（1）过C作CF⊥AB于F．
∵在Rt△ABC中，∠C＝90°，AC，tanB，∴BC＝2，由勾股定理得：AB1．
∵△ACB的面积S，∴CF2，∴CF为⊙C的半径．
∵CF⊥AB，∴AB为⊙C的切线；

（2）图中阴影部分的面积＝S△ACB﹣S扇形DCE1﹣π．
【点睛】
本题考查了勾股定理，扇形的面积，解直角三角形，切线的性质和判定等知识点，能求出CF的长是解答此题的关键．
23、-2（m+3），-1．
【解析】
此题的运算顺序：先括号里，经过通分，再约分化为最简，最后代值计算．
【详解】
解：（m+2-）•，
=，
=-，
=-2（m+3）．
把m=-代入，得，
原式=-2×（-+3）=-1．
24、（1）见解析；（2）tan∠CED＝
【解析】
（1）欲证明，只要证明即可；
（2）由，可得，设FO＝2a，OC＝3a，则DF＝a，DE＝1.5a，AD＝DB＝6a，由，可得BD•BE＝BC•BA，设AC＝BC＝x，则有，由此求出AC、CD即可解决问题.
【详解】
（1）证明：如下图，连接AE，
∵AD是直径，
∴，
∴DC⊥AB，
∵AC＝CB，
∴DA＝DB，
∴∠CDA＝∠CDB，
∵，，
∴∠BDC＝∠EAC，
∵∠AEC＝∠ADC，
∴∠EAC＝∠AEC，
∴；
（2）解：如下图，连接OC，
∵AO＝OD，AC＝CB，
∴OC∥BD，
∴，
∴，
设FO＝2a，OC＝3a，则DF＝a，DE＝1.5a，AD＝DB＝6a，
∵∠BAD＝∠BEC，∠B＝∠B，
∴，
∴BD•BE＝BC•BA，设AC＝BC＝x，
则有，
∴，
∴，
∴，
∴.

【点睛】
本题属于圆的综合题，涉及到三角形的相似，解直角三角形等相关考点，熟练掌握三角形相似的判定及解直角三角形等相关内容是解决本题的关键.
25、证明见解析.
【解析】
【分析】利用AAS先证明∆ABH≌∆DCG，根据全等三角形的性质可得AH=DG，再根据AH＝AG＋GH，DG＝DH＋GH即可证得AG＝HD.
【详解】∵AB∥CD，∴∠A＝∠D，
∵CE∥BF，∴∠AHB＝∠DGC，
在∆ABH和∆DCG中，
，
∴∆ABH≌∆DCG(AAS)，∴AH＝DG，
∵AH＝AG＋GH，DG＝DH＋GH，∴AG＝HD.
【点睛】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键.
26、（1）详见解析；（2）①详见解析；②.
【解析】
（1）根据轴对称的性质，可作出△ABC关于直线n的对称图形△A′B′C′；
（2）①作点B关于直线m的对称点B''，连接B''A与x轴的交点为点P；
②由△ABP的周长=AB+AP+BP=AB+AP+B''P，则当AP与PB''共线时，△APB的周长有最小值．
【详解】
解：（1）如图△A′B′C′为所求图形．

（2）①如图：点P为所求点．
②∵△ABP的周长=AB+AP+BP=AB+AP+B''P
∴当AP与PB''共线时，△APB的周长有最小值．
∴△APB的周长的最小值AB+AB''=+3
故答案为 +3
【点睛】
本题考查轴对称变换，勾股定理，最短路径问题，解题关键是熟练掌握轴对称的性质．
27、（1）①12，3. ②详见解析.（2）.
【解析】
分析：（1）①根据题意和表中的数据可以求得a的值；②由表格中的数据可以将频数分布表补充完整；
（2）根据表格中的数据和测试成绩不低于80分为优秀，可以求得优秀率；
（3）根据题意可以求得所有的可能性，从而可以得到小明与小强两名男同学能分在同一组的概率．
详解：（1）①a=50﹣（6+8+14+10）=12，
中位数为第25、26个数的平均数，而第25、26个数均落在第3组内，
所以中位数落在第3组，
故答案为12，3；
②如图，

（2）×100%=44%，
答：本次测试的优秀率是44%；
（3）设小明和小强分别为A、B，另外两名学生为：C、D，
则所有的可能性为：（AB﹣CD）、（AC﹣BD）、（AD﹣BC）.
所以小明和小强分在一起的概率为：．
点睛：本题考查列举法求概率、频数分布表、频数分布直方图、中位数，解题的关键是明确题意，找出所求问题需要的条件，可以将所有的可能性都写出来，求出相应的概率．