高中人教A版 (2019)5.3 导数在研究函数中的应用图文课件ppt

这是一份高中人教A版 (2019)5.3 导数在研究函数中的应用图文课件ppt，共35页。PPT课件主要包含了f′x0，极大值，极小值等内容，欢迎下载使用。
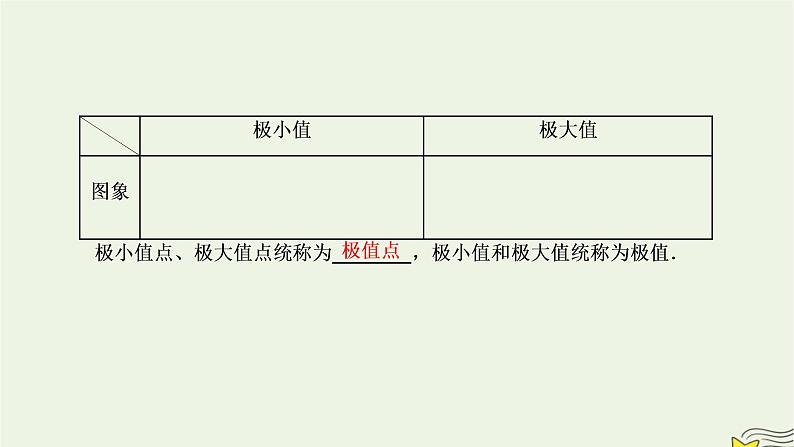
(一)教材梳理填空1．极小值、极大值的概念
[微提醒](1)极值是一个局部概念，极值只是某个点的函数值，与它附近点的函数值比较它是最大值或最小值，但并不意味着它在函数的整个定义域内是最大值或最小值．(2)一个函数在某区间上或定义域内的极大值或极小值可以不止一个．(3)函数的极大值与极小值之间无确定的大小关系．(4)函数的极值点一定出现在区间的内部，区间的端点不能成为极值点．(5)单调函数一定没有极值．
2．求函数y＝f(x)极值的方法一般地，求函数y＝f(x)的极值的方法是：解方程f′(x)＝0，当f′(x0)＝0时：(1)如果在x0附近的左侧f′(x)＞0，右侧f′(x)＜0，那么f(x0)是 ；(2)如果在x0附近的左侧f′(x)＜0，右侧f′(x)＞0，那么f(x0)是 ．
[微提醒]一般来说，“f′(x0)＝0”是“函数y＝f(x)在点x0处取得极值”的必要不充分条件．若可导函数y＝f(x)在点x0处可导，且在点x0处取得极值，那么f′(x0)＝0；反之，若f′(x0)＝0，则点x0不一定是函数y＝f(x)的极值点．
答案：(1)√　(2)√　(3)×
2．[多选]下列四个函数，在x＝0处取得极小值的是(　　)A．y＝x3 B．y＝x2＋1C．y＝|x| D．y＝2x答案：BC
题型一　极值的图象特征 [学透用活][典例1]　已知函数y＝f(x)，其导函数y＝f′(x)的图象如图所示，则y＝f(x)(　　)A．在(－∞，0)上为减函数B．在x＝0处取极小值C．在(4，＋∞)上为减函数D．在x＝2处取极大值
[解析]　由导函数的图象可知：x∈(－∞，0)∪(2,4)时，f′(x)>0；x∈(0,2)∪(4，＋∞)时，f′(x)0，于是f′(x)>0，故函数f(x)在区间(1，＋∞)上是增函数，A正确；当x∈(－1,0)时，xf′(x)>0，于是f′(x)