

辽宁省锦州市凌海市市级名校2021-2022学年中考猜题数学试卷含解析
展开2021-2022中考数学模拟试卷
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1.剪纸是我国传统的民间艺术,下列剪纸作品中既不是轴对称图形,也不是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A.a2·a3﹦a6 B.a3+ a3﹦a6 C.|-a2|﹦a2 D.(-a2)3﹦a6
3.姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图像经过第一象限;乙:函数图像经过第三象限;丙:在每一个象限内,y值随x值的增大而减小.根据他们的描述,姜老师给出的这个函数表达式可能是()
A. B. C. D.
4.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为( )
A.零上3℃ B.零下3℃ C.零上7℃ D.零下7℃
5.下列运算中,正确的是 ( )
A.x2+5x2=6x4 B.x3 C. D.
6.- 的绝对值是( )
A.-4 B. C.4 D.0.4
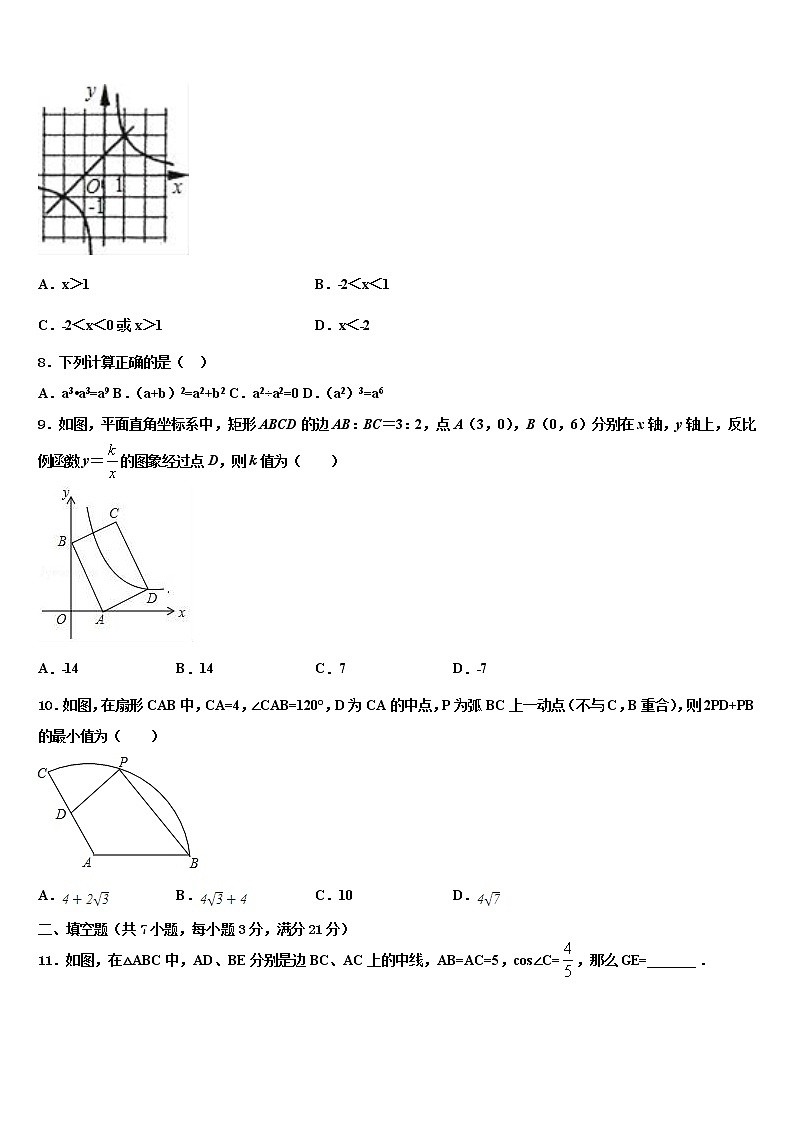
7.如图,是一次函数y=kx+b与反比例函数y=的图象,则关于x的不等式kx+b>的解集为
A.x>1 B.﹣2<x<1
C.﹣2<x<0或x>1 D.x<﹣2
8.下列计算正确的是( )
A.a3•a3=a9 B.(a+b)2=a2+b2 C.a2÷a2=0 D.(a2)3=a6
9.如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=的图象经过点D,则k值为( )
A.﹣14 B.14 C.7 D.﹣7
10.如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为弧BC上一动点(不与C,B重合),则2PD+PB的最小值为( )
A. B. C.10 D.
二、填空题(共7小题,每小题3分,满分21分)
11.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=,那么GE=_______.
12.若代数式x2﹣6x+b可化为(x+a)2﹣5,则a+b的值为____.
13.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是_____cm.
14.小华到商场购买贺卡,他身上带的钱恰好能买5张3D立体贺卡或20张普通贺卡若小华先买了3张3D立体贺卡,则剩下的钱恰好还能买______张普通贺卡.
15.如图,点M、N分别在∠AOB的边OA、OB上,将∠AOB沿直线MN翻折,设点O落在点P处,如果当OM=4,ON=3时,点O、P的距离为4,那么折痕MN的长为______.
16.已知图中Rt△ABC,∠B=90°,AB=BC,斜边AC上的一点D,满足AD=AB,将线段AC绕点A逆时针旋转α (0°<α <360°),得到线段AC’,连接DC’,当DC’//BC时,旋转角度α 的值为_________,
17.半径为2的圆中,60°的圆心角所对的弧的弧长为_____.
三、解答题(共7小题,满分69分)
18.(10分)如图,二次函数的图象与x轴的一个交点为,另一个交点为A,且与y轴相交于C点
求m的值及C点坐标;
在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由
为抛物线上一点,它关于直线BC的对称点为Q
当四边形PBQC为菱形时,求点P的坐标;
点P的横坐标为,当t为何值时,四边形PBQC的面积最大,请说明理由.
19.(5分)新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4 000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:降价8%,另外每套房赠送a元装修基金;降价10%,没有其他赠送.请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数表达式;老王要购买第十六层的一套房,若他一次性付清所有房款,请帮他计算哪种优惠方案更加合算.
20.(8分)每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
21.(10分)已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求:坡顶A到地面PO的距离;古塔BC的高度(结果精确到1米).
22.(10分)如图,对称轴为直线的抛物线与x轴相交于A、B两点,其中A点的坐标为(-3,0).
(1)求点B的坐标;
(2)已知,C为抛物线与y轴的交点.
①若点P在抛物线上,且,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
23.(12分)现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.求y与x之间的函数关系式;设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
24.(14分)某数学教师为了解所教班级学生完成数学课前预习的具体情况,对该班部分学生进行了一学期的跟踪调查,将调查结果分为四类并给出相应分数,A:很好,95分;B:较好75分;C:一般,60分;D:较差,30分.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(Ⅰ)该教师调查的总人数为 ,图②中的m值为 ;
(Ⅱ)求样本中分数值的平均数、众数和中位数.
参考答案
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1、C
【解析】
【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.
【详解】A、不是中心对称图形,是轴对称图形,故本选项错误;
B、不是中心对称图形,是轴对称图形,故本选项错误;
C、既不是中心对称图形,也不是轴对称图形,故本选项正确;
D、是中心对称图形,不是轴对称图形,故本选项错误,
故选C.
【点睛】本题主要考查轴对称图形和中心对称图形,在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;在平面内,如果把一个图形绕某个点旋转180°后,能与原图形重合,那么就说这个图形是中心对称图形.
2、C
【解析】
根据同底数幂相乘,底数不变指数相加;合并同类项,只把系数相加减,字母与字母的次数不变;同底数幂相除,底数不变指数相减,对各选项计算后利用排除法求解.
【详解】
a2·a3﹦a5,故A项错误;a3+ a3﹦2a3,故B项错误;a3+ a3﹦- a6,故D项错误,选C.
【点睛】
本题考查同底数幂加减乘除及乘方,解题的关键是清楚运算法则.
3、B
【解析】
y=3x的图象经过一三象限过原点的直线,y随x的增大而增大,故选项A错误;
y=的图象在一、三象限,在每个象限内y随x的增大而减小,故选项B正确;
y=−的图象在二、四象限,故选项C错误;
y=x²的图象是顶点在原点开口向上的抛物线,在一、二象限,故选项D错误;
故选B.
4、B
【解析】
试题分析:由题意知,“-”代表零下,因此-3℃表示气温为零下3℃.
故选B.
考点:负数的意义
5、C
【解析】
分析:直接利用积的乘方运算法则及合并同类项和同底数幂的乘除运算法则分别分析得出结果.
详解:A. x2+5x2= ,本项错误;B. ,本项错误;C. ,正确;
D.,本项错误.故选C.
点睛:本题主要考查了积的乘方运算及合并同类项和同底数幂的乘除运算,解答本题的关键是正确掌握运算法则.
6、B
【解析】
直接用绝对值的意义求解.
【详解】
−的绝对值是.
故选B.
【点睛】
此题是绝对值题,掌握绝对值的意义是解本题的关键.
7、C
【解析】
根据反比例函数与一次函数在同一坐标系内的图象可直接解答.
【详解】
观察图象,两函数图象的交点坐标为(1,2),(-2,-1),kx+b>的解就是一次函数y=kx+b图象在反比例函数y=的图象的上方的时候x的取值范围,
由图象可得:-2<x<0或x>1,
故选C.
【点睛】
本题考查的是反比例涵数与一次函数图象在同一坐标系中二者的图象之间的关系.一般这种类型的题不要计算反比计算表达式,解不等式,直接从从图象上直接解答.
8、D.
【解析】
试题分析:A、原式=a6,不符合题意;B、原式=a2+2ab+b2,不符合题意;
C、原式=1,不符合题意;D、原式=a6,符合题意,
故选D
考点:整式的混合运算
9、B
【解析】
过点D作DF⊥x轴于点F,则∠AOB=∠DFA=90°,∴∠OAB+∠ABO=90°,
∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC,∴∠OAB+∠DAF=90°,∴∠ABO=∠DAF,
∴△AOB∽△DFA,∴OA:DF=OB:AF=AB:AD,
∵AB:BC=3:2,点A(3,0),B(0,6),∴AB:AD=3:2,OA=3,OB=6,∴DF=2,AF=4,∴OF=OA+AF=7,∴点D的坐标为:(7,2),∴k,故选B.
10、D
【解析】
如图,作∥∠PAP′=120°,则AP′=2AB=8,连接PP′,BP′,则∠1=∠2,推出△APD∽△ABP′,得到BP′=2PD,于是得到2PD+PB=BP′+PB≥PP′,根据勾股定理得到PP′=,求得2PD+PB≥4,于是得到结论.
【详解】
如图,作∥∠PAP′=120°,则AP′=2AB=8,连接PP′,BP′,
则∠1=∠2,
∵=2,
∴△APD∽△ABP′,
∴BP′=2PD,
∴2PD+PB=BP′+PB≥PP′,
∴PP′=,
∴2PD+PB≥4,
∴2PD+PB的最小值为4,
故选D.
【点睛】
本题考查了轴对称-最短距离问题,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
二、填空题(共7小题,每小题3分,满分21分)
11、
【解析】
过点E作EF⊥BC交BC于点F,分别求得AD=3,BD=CD=4,EF=,DF=2,BF=6,再结合△BGD∽△BEF即可.
【详解】
过点E作EF⊥BC交BC于点F.
∵AB=AC, AD为BC的中线 ∴AD⊥BC ∴EF为△ADC的中位线.
又∵cos∠C=,AB=AC=5,∴AD=3,BD=CD=4,EF=,DF=2
∴BF=6
∴在Rt△BEF中BE==,
又∵△BGD∽△BEF
∴,即BG=.
GE=BE-BG=
故答案为.
【点睛】
本题考查的知识点是三角形的相似,解题的关键是熟练的掌握三角形的相似.
12、1
【解析】
根据题意找到等量关系x2﹣6x+b=(x+a)2﹣5,根据系数相等求出a,b,即可解题.
【详解】
解:由题可知x2﹣6x+b=(x+a)2﹣5,
整理得:x2﹣6x+b= x2+2ax+a2-5,
即-6=2a,b= a2-5,
解得:a=-3,b=4,
∴a+b=1.
【点睛】
本题考查了配方法的实际应用,属于简单题,找到等量关系求出a,b是解题关键.
13、40cm
【解析】
首先根据圆锥的底面直径求得圆锥的底面周长,然后根据底面周长等于展开扇形的弧长求得铁皮的半径即可.
【详解】
∵圆锥的底面直径为60cm,
∴圆锥的底面周长为60πcm,
∴扇形的弧长为60πcm,
设扇形的半径为r,
则=60π,
解得:r=40cm,
故答案为:40cm.
【点睛】
本题考查了圆锥的计算,解题的关键是首先求得圆锥的底面周长,利用圆锥的底面周长等于扇形的弧长求解.
14、1
【解析】
根据已知他身上带的钱恰好能买5张3D立体贺卡或20张普通贺卡得:1张3D立体贺卡的单价是1张普通贺卡单价的4倍,所以设1张3D立体贺卡x元,剩下的钱恰好还能买y张普通贺卡,根据3张3D立体贺卡张普通贺卡张3D立体贺卡,可得结论.
【详解】
解:设1张3D立体贺卡x元,剩下的钱恰好还能买y张普通贺卡.
则1张普通贺卡为:元,
由题意得:,
,
答:剩下的钱恰好还能买1张普通贺卡.
故答案为:1.
【点睛】
本题考查了一元一次方程的应用以及列代数式,解题的关键是:根据总价单价数量列式计算.
15、
【解析】
由折叠的性质可得MN⊥OP,EO=EP=2,由勾股定理可求ME,NE的长,即可求MN的长.
【详解】
设MN与OP交于点E,
∵点O、P的距离为4,
∴OP=4
∵折叠
∴MN⊥OP,EO=EP=2,
在Rt△OME中,ME=
在Rt△ONE中,NE=
∴MN=ME-NE=2-
故答案为2-
【点睛】
本题考查了翻折变换,勾股定理,利用勾股定理求线段的长度是本题的关键.
16、15或255°
【解析】
如下图,设直线DC′与AB相交于点E,
∵Rt△ABC中,∠B=90°,AB=BC,DC′//BC,
∴∠AED=∠ABC=90°,∠ADE=∠ACB=∠BAC=45°,AB=AC,
∴AE=AD,
又∵AD=AB,AC′=AC,
∴AE=AB=AC=AC′,
∴∠C′=30°,
∴∠EAC′=60°,
∴∠CAC′=60°-45°=15°, 即当DC′∥BC时,旋转角=15°;
同理,当DC′′∥BC时,旋转角=180°-45°-60°=255°;
综上所述,当旋转角=15°或255°时,DC′//BC.
故答案为:15°或255°.
17、
【解析】
根据弧长公式可得:=,
故答案为.
三、解答题(共7小题,满分69分)
18、,;存在,;或;当时,.
【解析】
(1)用待定系数法求出抛物线解析式;
(2)先判断出面积最大时,平移直线BC的直线和抛物线只有一个交点,从而求出点M坐标;
(3)①先判断出四边形PBQC时菱形时,点P是线段BC的垂直平分线,利用该特殊性建立方程求解;
②先求出四边形PBCQ的面积与t的函数关系式,从而确定出它的最大值.
【详解】
解:(1)将B(4,0)代入,解得,m=4,
∴二次函数解析式为,令x=0,得y=4,
∴C(0,4);
(2)存在,理由:∵B(4,0),C(0,4),
∴直线BC解析式为y=﹣x+4,当直线BC向上平移b单位后和抛物线只有一个公共点时,△MBC面积最大,
∴,
∴,
∴△=1﹣4b=0,∴b=4,
∴,∴M(2,6);
(3)①如图,∵点P在抛物线上,
∴设P(m,),当四边形PBQC是菱形时,点P在线段BC的垂直平分线上,∵B(4,0),C(0,4),
∴线段BC的垂直平分线的解析式为y=x,
∴m=,
∴m=,
∴P(,)或P(,);
②如图,设点P(t,),过点P作y轴的平行线l,过点C作l的垂线,
∵点D在直线BC上,∴D(t,﹣t+4),
∵PD=﹣(﹣t+4)=,BE+CF=4,
∴S四边形PBQC=2S△PDC=2(S△PCD+S△BD)=2(PD×CF+PD×BE)=4PD=
∵0<t<4,
∴当t=2时,S四边形PBQC最大=1.
考点:二次函数综合题;二次函数的最值;最值问题;分类讨论;压轴题.
19、(1) ;(2)当每套房赠送的装修基金多于10 560元时,选择方案一合算;当每套房赠送的装修基金等于10 560元时,两种方案一样;当每套房赠送的装修基金少于10 560元时,选择方案二合算.
【解析】
解:(1)当1≤x≤8时,每平方米的售价应为:
y=4000﹣(8﹣x)×30="30x+3760" (元/平方米)
当9≤x≤23时,每平方米的售价应为:
y=4000+(x﹣8)×50=50x+3600(元/平方米).
∴
(2)第十六层楼房的每平方米的价格为:50×16+3600=4400(元/平方米),
按照方案一所交房款为:W1=4400×120×(1﹣8%)﹣a=485760﹣a(元),
按照方案二所交房款为:W2=4400×120×(1﹣10%)=475200(元),
当W1>W2时,即485760﹣a>475200,
解得:0<a<10560,
当W1<W2时,即485760﹣a<475200,
解得:a>10560,
∴当0<a<10560时,方案二合算;当a>10560时,方案一合算.
【点睛】
本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.
20、(1)2000;(2)28.8°;(3)补图见解析;(4)36万人.
【解析】
分析:(1)将A选项人数除以总人数即可得;
(2)用360°乘以E选项人数所占比例可得;
(3)用总人数乘以D选项人数所占百分比求得其人数,据此补全图形即可得;
(4)用总人数乘以样本中C选项人数所占百分比可得.
详解:(1)本次接受调查的市民人数为300÷15%=2000人,
(2)扇形统计图中,扇形E的圆心角度数是360°×=28.8°,
(3)D选项的人数为2000×25%=500,
补全条形图如下:
(4)估计赞同“选育无絮杨品种,并推广种植”的人数为90×40%=36(万人).
点睛:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21、 (1)坡顶到地面的距离为米;移动信号发射塔的高度约为米.
【解析】
延长BC交OP于H.在Rt△APD中解直角三角形求出AD=10.PD=24.由题意BH=PH.设BC=x.则x+10=24+DH.推出AC=DH=x﹣14.在Rt△ABC中.根据tan76°=,构建方程求出x即可.
【详解】
延长BC交OP于H.
∵斜坡AP的坡度为1:2.4,
∴,
设AD=5k,则PD=12k,由勾股定理,得AP=13k,
∴13k=26,
解得k=2,
∴AD=10,
∵BC⊥AC,AC∥PO,
∴BH⊥PO,
∴四边形ADHC是矩形,CH=AD=10,AC=DH,
∵∠BPD=45°,
∴PH=BH,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=,即≈4.1.
解得:x≈18.7,
经检验x≈18.7是原方程的解.
答:古塔BC的高度约为18.7米.
【点睛】
本题主要考查了解直角三角形,用到的知识点是勾股定理,锐角三角函数,坡角与坡角等,解决本题的关键是作出辅助线,构造直角三角形.
22、(1)点B的坐标为(1,0).
(2)①点P的坐标为(4,21)或(-4,5).
②线段QD长度的最大值为.
【解析】
(1)由抛物线的对称性直接得点B的坐标.
(2)①用待定系数法求出抛物线的解析式,从而可得点C的坐标,得到,设出点P 的坐标,根据列式求解即可求得点P的坐标.
②用待定系数法求出直线AC的解析式,由点Q在线段AC上,可设点Q的坐标为(q,-q-3),从而由QD⊥x轴交抛物线于点D,得点D的坐标为(q,q2+2q-3),从而线段QD等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解.
【详解】
解:(1)∵A、B两点关于对称轴对称 ,且A点的坐标为(-3,0),
∴点B的坐标为(1,0).
(2)①∵抛物线,对称轴为,经过点A(-3,0),
∴,解得.
∴抛物线的解析式为.
∴B点的坐标为(0,-3).∴OB=1,OC=3.∴.
设点P的坐标为(p,p2+2p-3),则.
∵,∴,解得.
当时;当时,,
∴点P的坐标为(4,21)或(-4,5).
②设直线AC的解析式为,将点A,C的坐标代入,得:
,解得:.
∴直线AC的解析式为.
∵点Q在线段AC上,∴设点Q的坐标为(q,-q-3).
又∵QD⊥x轴交抛物线于点D,∴点D的坐标为(q,q2+2q-3).
∴.
∵,
∴线段QD长度的最大值为.
23、(1);(2)①;②
【解析】
(1)先求出种植C种树苗的人数,根据现种植A、B、C三种树苗一共480棵,可以列出等量关系,解出y与x之间的关系;
(2)①分别求出种植A,B,C三种树苗的成本,然后相加即可;
②求出种植C种树苗工人的人数,然后用种植C种树苗工人的人数÷总人数即可求出概率.
【详解】
解:(1)设种植A种树苗的工人为x名,种植B种树苗的工人为y名,则种植C种树苗的人数为(80-x-y)人,
根据题意,得:8x+6y+5(80-x-y)=480,
整理,得:y=-3x+80;
(2)①w=15×8x+12×6y+8×5(80-x-y)=80x+32y+3200,
把y=-3x+80代入,得:w=-16x+5760,
②种植的总成本为5600元时,w=-16x+5760=5600,
解得x=10,y=-3×10+80=50,
即种植A种树苗的工人为10名,种植B种树苗的工人为50名,种植B种树苗的工人为:80-10-50=20名.
采访到种植C种树苗工人的概率为:=.
【点睛】
本题主要考查了一次函数的实际问题,以及概率的求法,能够将实际问题转化成数学模型是解答此题的关键.
24、(Ⅰ)25、40;(Ⅱ)平均数为68.2分,众数为75分,中位数为75分.
【解析】
(1)由直方图可知A的总人数为5,再依据其所占比例20%可求解总人数;由直方图中B的人数为10及总人数可知m的值;
(2)根据平均数、众数和中位数的定义求解即可.
【详解】
(Ⅰ)该教师调查的总人数为(2+3)÷20%=25(人),
m%=×100%=40%,即m=40,
故答案为:25、40;
(Ⅱ)由条形图知95分的有5人、75分的有10人、60分的有6人、30分的有4人,
则样本分知的平均数为(分),
众数为75分,中位数为第13个数据,即75分.
【点睛】
理解两幅统计图中各数据的含义及其对应关系是解题关键.
浙江省江北区市级名校2021-2022学年中考猜题数学试卷含解析: 这是一份浙江省江北区市级名校2021-2022学年中考猜题数学试卷含解析,共19页。
陕西省三原县市级名校2021-2022学年中考猜题数学试卷含解析: 这是一份陕西省三原县市级名校2021-2022学年中考猜题数学试卷含解析,共22页。试卷主要包含了考生要认真填写考场号和座位序号,已知,则的值为,下列命题正确的是等内容,欢迎下载使用。
辽宁省鞍山市市级名校2021-2022学年中考数学猜题卷含解析: 这是一份辽宁省鞍山市市级名校2021-2022学年中考数学猜题卷含解析,共24页。试卷主要包含了考生要认真填写考场号和座位序号,下列计算正确的是等内容,欢迎下载使用。












