三门峡实验中学2022年中考猜题数学试卷含解析

2021-2022中考数学模拟试卷

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1．若分式有意义，则a的取值范围为(   )

A．a≠4 B．a＞4 C．a＜4 D．a＝4

2．一、单选题

如图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（　　）

A．点A B．点B C．点C D．点D

3．下列博物院的标识中不是轴对称图形的是（    ）

A． B．

C． D．

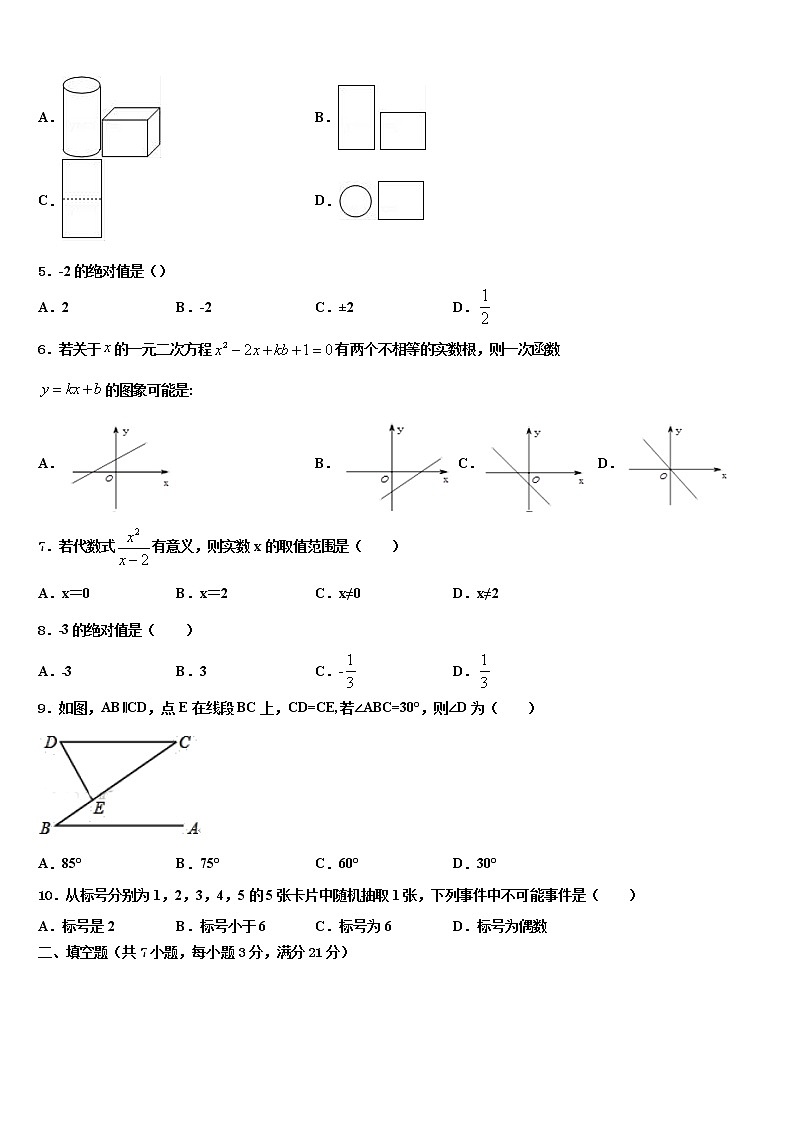
4．如图，水平的讲台上放置的圆柱体笔筒和正方体粉笔盒，其左视图是（　　）

A． B．

C． D．

5．-2的绝对值是（）

A．2 B．-2 C．±2 D．

6．若关于的一元二次方程有两个不相等的实数根，则一次函数

的图象可能是:

A． B． C． D．

7．若代数式有意义，则实数x的取值范围是（    ）

A．x＝0 B．x＝2 C．x≠0 D．x≠2

8．﹣3的绝对值是（　　）

A．﹣3 B．3 C．- D．

9．如图，AB∥CD，点E在线段BC上，CD=CE,若∠ABC=30°，则∠D为（　　）

A．85° B．75° C．60° D．30°

10．从标号分别为1，2，3，4，5的5张卡片中随机抽取1张，下列事件中不可能事件是（　　）

A．标号是2 B．标号小于6 C．标号为6 D．标号为偶数

二、填空题（共7小题，每小题3分，满分21分）

11．如图，若∠1+∠2=180°，∠3=110°，则∠4=           ．

12．在△ABC中，MN∥BC 分别交AB，AC于点M，N；若AM=1，MB=2，BC=3，则MN的长为_____．

13．如图，二次函数y=a（x﹣2）2+k（a＞0）的图象过原点，与x轴正半轴交于点A，矩形OABC的顶点C的坐标为（0，﹣2），点P为x轴上任意一点，连结PB、PC．则△PBC的面积为_____．

14．如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点，将Rt△ABC沿CD折叠，使点B落在AC边上的B′处，则∠ADB′等于_____．

15．在中，,，点分别是边的中点，则的周长是__________．

16．如图，垂直于x轴的直线AB分别与抛物线C1：y＝x2（x≥0）和抛物线C2：y＝（x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C、D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E、F，则 的值为_____．

17．计算：﹣22÷（﹣）=_____．

三、解答题（共7小题，满分69分）

18．（10分）如图，在平面直角坐标系中，A为y轴正半轴上一点，过点A作x轴的平行线，交函数的图象于B点，交函数的图象于C，过C作y轴和平行线交BO的延长线于D．

（1）如果点A的坐标为（0，2），求线段AB与线段CA的长度之比；

（2）如果点A的坐标为（0，a），求线段AB与线段CA的长度之比；

（3）在（1）条件下，四边形AODC的面积为多少？

19．（5分）（1）（﹣2）2+2sin 45°﹣

（2）解不等式组，并将其解集在如图所示的数轴上表示出来．

20．（8分）    某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．

(1)请你用直尺和圆规作出这个输水管道的圆形截面的圆心(保留作图痕迹)；

(2)若这个输水管道有水部分的水面宽AB＝8 cm，水面最深地方的高度为2 cm，求这个圆形截面的半径．

21．（10分）如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC交于点D，过点D作∠ABD=∠ADE，交AC于点E．

(1)求证：DE为⊙O的切线．

(2)若⊙O的半径为，AD=，求CE的长．

22．（10分）如图，在中，,以边为直径作⊙交边于点,过点作于点，、的延长线交于点.

求证：是⊙的切线；若,且,求⊙的半径与线段的长.

23．（12分）如图，分别延长▱ABCD的边到，使，连接EF，分别交于，连结求证：．

24．（14分）新定义：如图1（图2，图3），在△ABC中，把AB边绕点A顺时针旋转，把AC边绕点A逆时针旋转，得到△AB′C′，若∠BAC+∠B′AC′=180°，我们称△ABC是△AB′C′的“旋补三角形”，△AB'C′的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”

（特例感知）（1）①若△ABC是等边三角形（如图2），BC=1，则AD=　   　；

②若∠BAC=90°（如图3），BC=6，AD=　   　；

（猜想论证）（2）在图1中，当△ABC是任意三角形时，猜想AD与BC的数量关系，并证明你的猜想；

（拓展应用）（3）如图1．点A，B，C，D都在半径为5的圆上，且AB与CD不平行，AD=6，点P是四边形ABCD内一点，且△APD是△BPC的“旋补三角形”，点P是“旋补中心”，请确定点P的位置（要求尺规作图，不写作法，保留作图痕迹），并求BC的长．

参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）

1、A

【解析】
分式有意义时，分母a-4≠0

【详解】

依题意得：a−4≠0，

解得a≠4.

故选：A

【点睛】

此题考查分式有意义的条件，难度不大

2、D

【解析】
根据全等三角形的性质和已知图形得出即可．

【详解】

解：∵△MNP≌△MEQ，

∴点Q应是图中的D点，如图，

故选：D．

【点睛】

本题考查了全等三角形的性质，能熟记全等三角形的性质的内容是解此题的关键，注意：全等三角形的对应角相等，对应边相等．

3、A

【解析】
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,对题中选项进行分析即可.

【详解】

A、不是轴对称图形，符合题意；

B、是轴对称图形，不合题意；

C、是轴对称图形，不合题意；

D、是轴对称图形，不合题意；

故选：A．

【点睛】

此题考查轴对称图形的概念，解题的关键在于利用轴对称图形的概念判断选项正误

4、C

【解析】
根据左视图是从物体的左面看得到的视图解答即可．

【详解】

解：水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒，其左视图是一个含虚线的

长方形，

故选C．

【点睛】

本题考查的是几何体的三视图，左视图是从物体的左面看得到的视图．

5、A

【解析】
根据绝对值的性质进行解答即可

【详解】

解：﹣1的绝对值是：1．

故选：A．

【点睛】

此题考查绝对值，难度不大

6、B

【解析】
由方程有两个不相等的实数根,

可得，

解得，即异号，

当时，一次函数的图象过一三四象限，

当时，一次函数的图象过一二四象限，故答案选B.

7、D

【解析】
根据分式的分母不等于0即可解题.

【详解】

解：∵代数式有意义，

∴x-2≠0,即x≠2,

故选D.

【点睛】

本题考查了分式有意义的条件,属于简单题,熟悉分式有意义的条件是解题关键.

8、B

【解析】
根据负数的绝对值是它的相反数，可得出答案.

【详解】

根据绝对值的性质得：|-1|=1．

故选B．

【点睛】

本题考查绝对值的性质，需要掌握非负数的绝对值是它本身，负数的绝对值是它的相反数.

9、B

【解析】

分析：先由AB∥CD，得∠C=∠ABC=30°，CD=CE，得∠D=∠CED，再根据三角形内角和定理得，∠C+∠D+∠CED=180°，即30°+2∠D=180°，从而求出∠D．

详解：∵AB∥CD，

∴∠C=∠ABC=30°，

又∵CD=CE，

∴∠D=∠CED，

∵∠C+∠D+∠CED=180°，即30°+2∠D=180°，

∴∠D=75°．

故选B．

点睛：此题考查的是平行线的性质及三角形内角和定理，解题的关键是先根据平行线的性质求出∠C，再由CD=CE得出∠D=∠CED，由三角形内角和定理求出∠D．

10、C

【解析】
利用随机事件以及必然事件和不可能事件的定义依次分析即可解答．

【详解】

选项A、标号是2是随机事件；

选项B、该卡标号小于6是必然事件；

选项C、标号为6是不可能事件；

选项D、该卡标号是偶数是随机事件；

故选C．

【点睛】

本题考查了随机事件以及必然事件和不可能事件的定义，正确把握相关定义是解题关键．

二、填空题（共7小题，每小题3分，满分21分）

11、110°．

【解析】
解：∵∠1+∠2=180°，

∴a∥b，∴∠3=∠4，

又∵∠3=110°，∴∠4=110°．

故答案为110°．

12、1

【解析】
∵MN∥BC，

∴△AMN∽△ABC，

∴，即，

∴MN=1.

故答案为1.

13、4

【解析】
根据二次函数的对称性求出点A的坐标，从而得出BC的长度，根据点C的坐标得出三角形的高线，从而得出答案．

【详解】

∵二次函数的对称轴为直线x=2， ∴点A的坐标为(4，0)，∵点C的坐标为(0，－2)，

∴点B的坐标为(4，－2)， ∴BC=4，则．

【点睛】

本题主要考查的是二次函数的对称性，属于基础题型．理解二次函数的轴对称性是解决这个问题的关键．

14、40°．

【解析】
∵将Rt△ABC沿CD折叠，使点B落在AC边上的B′处，

∴∠ACD=∠BCD，∠CDB=∠CDB′，

∵∠ACB=90°，∠A=25°，

∴∠ACD=∠BCD=45°，∠B=90°﹣25°=65°，

∴∠BDC=∠B′DC=180°﹣45°﹣65°=70°，

∴∠ADB′=180°﹣70°﹣70°=40°．

故答案为40°．

15、

【解析】
首先利用勾股定理求得斜边长，然后利用三角形中位线定理求得答案即可．

【详解】

解：∵Rt△ABC中，∠C=90°，AC=3，BC=4，

∴AB===5，

∵点D、E、F分别是边AB、AC、BC的中点，

∴DE=BC，DF=AC，EF=AB，

∴C△DEF=DE+DF+EF=BC +AC +AB = (BC+AC+AB)=(4+3+5)=6.

故答案为：6.

【点睛】

本题考查了勾股定理和三角形中位线定理.

16、

【解析】
根据二次函数的图象和性质结合三角形面积公式求解.

【详解】

解：设点横坐标为，则点纵坐标为，点B的纵坐标为 ，

∵BE∥x轴，

∴点F纵坐标为，

∵点F是抛物线上的点，

∴点F横坐标为，

∵轴，

∴点D纵坐标为，

∵点D是抛物线上的点，

∴点D横坐标为，

，

故答案为．

【点睛】

此题重点考查学生对二次函数的图象和性质的应用能力，熟练掌握二次函数的图象和性质是解题的关键.

17、1

【解析】

解：原式==1．故答案为1．

三、解答题（共7小题，满分69分）

18、（1）线段AB与线段CA的长度之比为；（2）线段AB与线段CA的长度之比为；（3）1．

【解析】

试题分析：

（1）由题意把y=2代入两个反比例函数的解析式即可求得点B、C的横坐标，从而得到AB、AC的长，即可得到线段AB与AC的比值；

（2）由题意把y=a代入两个反比例函数的解析式即可求得用“a”表示的点B、C的横坐标，从而可得到AB、AC的长，即可得到线段AB与AC的比值；

（3）由（1）可知，AB:AC=1:3，由此可得AB:BC=1:4，利用OA=2和平行线分线段成比例定理即可求得CD的长，从而可由梯形的面积公式求出四边形AODC的面积.

试题解析：

（1）∵A（0，2），BC∥x轴，

∴B（﹣1，2），C（3，2），

∴AB=1，CA=3，

∴线段AB与线段CA的长度之比为；

（2）∵B是函数y=﹣（x＜0）的一点，C是函数y=（x＞0）的一点，

∴B（﹣，a），C（，a），

∴AB=，CA=，

∴线段AB与线段CA的长度之比为；

（3）∵=，

∴=，

又∵OA=a，CD∥y轴，

∴，

∴CD=4a，

∴四边形AODC的面积为=（a+4a）×=1． 

19、（1）4﹣5；﹣＜x≤2，在数轴上表示见解析

【解析】
（1）此题涉及乘方、特殊角的三角函数、负整数指数幂和二次根式的化简，首先针对各知识点进行计算，再计算实数的加减即可；

（2）首先解出两个不等式的解集，再根据大小小大中间找确定不等式组的解集．

【详解】

解：（1）原式=4+2×﹣2×3=4+﹣6=4﹣5；

（2），

解①得：x＞﹣，

解②得：x≤2，

不等式组的解集为：﹣＜x≤2，

在数轴上表示为：

．

【点睛】

此题主要考查了解一元一次不等式组，以实数的运算，关键是正确确定两个不等式的解集，掌握特殊角的三角函数值．

20、（1）详见解析；（2）这个圆形截面的半径是5 cm.

【解析】
（1）根据尺规作图的步骤和方法做出图即可；

（2）先过圆心作半径，交于点，设半径为，得出、的长，在中，根据勾股定理求出这个圆形截面的半径.

【详解】

(1)如图，作线段AB的垂直平分线l，与弧AB交于点C，作线段AC的垂直平分线l′与直线l交于点O，点O即为所求作的圆心．

(2)如图，过圆心O作半径CO⊥AB，交AB于点D，

设半径为r，则AD＝AB＝4，OD＝r－2，

在Rt△AOD中，r2＝42＋(r－2)2，解得r＝5，

答：这个圆形截面的半径是5 cm.

【点睛】

此题考查了垂径定理和勾股定理，关键是根据题意画出图形，再根据勾股定理进行求解.

21、 (1)证明见解析；(2)CE=1．

【解析】
（1）求出∠ADO+∠ADE=90°，推DE⊥OD，根据切线的判定推出即可；

（2）求出CD，AC的长，证△CDE∽△CAD，得出比例式，求出结果即可．

【详解】

(1)连接OD，

∵AB是直径，

∴∠ADB=90°，

∴∠ADO+∠BDO=90°，

∵OB=OD，

∴∠BDO=∠ABD，

∵∠ABD=∠ADE，

∴∠ADO+∠ADE=90°，

即，OD⊥DE，

∵OD为半径，

∴DE为⊙O的切线；

(2)∵⊙O的半径为，

∴AB=2OA==AC，

∵∠ADB=90°，

∴∠ADC=90°，

在Rt△ADC中，由勾股定理得：DC===5，

∵∠ODE=∠ADC=90°，∠ODB=∠ABD=∠ADE，

∴∠EDC=∠ADO，

∵OA=OD，

∴∠ADO=∠OAD，

∵AB=AC，AD⊥BC，

∴∠OAD=∠CAD，

∴∠EDC=∠CAD，

∵∠C=∠C，

∴△CDE∽△CAD，

∴=，

∴=，

解得：CE=1．

【点睛】

本题考查了等腰三角形的性质与切线的判定，解题的关键是熟练的掌握等腰三角形的性质与切线的判定.

22、（1）证明参见解析；（2）半径长为，=.

【解析】
（1）已知点D在圆上，要连半径证垂直，连结，则，所以，∵，∴.∴，∴∥.由得出，于是得出结论；（2）由得到，设，则.，，，由，解得值，进而求出圆的半径及AE长.

【详解】

解：（1）已知点D在圆上，要连半径证垂直，如图2所示，连结，∵，∴.∵，∴.∴，∴∥.∵，∴.∴是⊙的切线；（2）在和中，∵，∴. 设，则.∴，.∵，∴.∴，解得=，则3x=,AE=6×-=6,∴⊙的半径长为，=.

【点睛】

1.圆的切线的判定；2.锐角三角函数的应用.

23、证明见解析

【解析】

分析：根据平行四边形的性质以及已知的条件得出△EGD和△FHB全等，从而得出DG=BH，从而说明AG和CH平行且相等，得出四边形AHCG为平行四边形，从而得出答案．

详解：证明：在▱ABCD中，，

，又 ，≌，

，，又，

四边形AGCH为平行四边形， ．

点睛：本题主要考查的是平行四边形的性质以及判定定理，属于基础题型．解决这个问题的关键就是根据平行四边形的性质得出四边形AHCG为平行四边形．

24、（1）①2；②3；（2）AD=BC；（3）作图见解析；BC=4；

【解析】
（1）①根据等边三角形的性质可得出AB=AC=1、∠BAC=60，结合“旋补三角形”的定义可得出AB′=AC′=1、∠B′AC′=120°，利用等腰三角形的三线合一可得出∠ADC′=90°，通过解直角三角形可求出AD的长度；
②由“旋补三角形”的定义可得出∠B′AC′=90°=∠BAC、AB=AB′、AC=AC′，进而可得出△ABC≌△AB′C′（SAS），根据全等三角形的性质可得出B′C′=BC=6，再利用直角三角形斜边上的中线等于斜边的一半即可求出AD的长度；（2）AD=BC，过点B′作B′E∥AC′，且B′E=AC′，连接C′E、DE，则四边形ACC′B′为平行四边形，根据平行四边形的性质结合“旋补三角形”的定义可得出∠BAC=∠AB′E、BA=AB′、CA=EB′，进而可证出△BAC≌△AB′E（SAS），根据全等三角形的性质可得出BC=AE，由平行四边形的对角线互相平分即可证出AD=BC；（3）作AB、CD的垂直平分线，交于点P，则点P为四边形ABCD的外角圆圆心，过点P作PF⊥BC于点F，由（2）的结论可求出PF的长度，在Rt△BPF中，利用勾股定理可求出BF的长度，进而可求出BC的长度．

【详解】

（1）①∵△ABC是等边三角形，BC=1，

∴AB=AC=1，∠BAC=60，

∴AB′=AC′=1，∠B′AC′=120°．

∵AD为等腰△AB′C′的中线，

∴AD⊥B′C′，∠C′=30°，

∴∠ADC′=90°．

在Rt△ADC′中，∠ADC′=90°，AC′=1，∠C′=30°，

∴AD=AC′=2．

②∵∠BAC=90°，

∴∠B′AC′=90°．

在△ABC和△AB′C′中，，

∴△ABC≌△AB′C′（SAS），

∴B′C′=BC=6，

∴AD=B′C′=3．

故答案为：①2；②3．

（2）AD=BC．

证明：在图1中，过点B′作B′E∥AC′，且B′E=AC′，连接C′E、DE，则四边形ACC′B′为平行四边形．

∵∠BAC+∠B′AC′=140°，∠B′AC′+∠AB′E=140°，

∴∠BAC=∠AB′E．

在△BAC和△AB′E中，，

∴△BAC≌△AB′E（SAS），

∴BC=AE．

∵AD=AE，

∴AD=BC．

（3）在图1中，作AB、CD的垂直平分线，交于点P，则点P为四边形ABCD的外接圆圆心，过点P作PF⊥BC于点F．

∵PB=PC，PF⊥BC，

∴PF为△PBC的中位线，

∴PF=AD=3．

在Rt△BPF中，∠BFP=90°，PB=5，PF=3，

∴BF==1，

∴BC=2BF=4．

【点睛】

本题考查了等边三角形的性质、等腰三角形的判定与性质、平行四边形的性质、解直角三角形、勾股定理以及全等三角形的判定与性质，解题的关键是：（1）①利用解含30°角的直角三角形求出AD=AC′；②牢记直角三角形斜边上的中线等于斜边的一半；（2）构造平行四边形，利用平行四边形对角线互相平分找出AD=AE=BC；（3）利用（2）的结论结合勾股定理求出BF的长度．