初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt

这是一份初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt，共31页。PPT课件主要包含了复习巩固，回顾一，相似多边形，定义性质，重点回顾，回顾二，相似三角形，回顾三，相似三角形的应用，回顾四等内容，欢迎下载使用。
通过对本章的学习，你学习了哪些知识？
两个边数相同的多边形，如果它们的角分别相等，边成比例，那么这两个多边形叫做相似多边形。
相似多边形的对应角相等,对应边的长度成比例。
对应角相等，对应边的比相等的两个三角形相似。
平行于三角形一边的直线所截得的三角形与原三角形相似。
两角分别对应相等的两个三角形相似。两组对应边的比相等且夹角相等的两个三角形相似。三组对应边的比相等的两个三角形相似。
对应角相等，对应边的比相等。对应高的比、中线的比、角平分线的比都等于相似比。周长的比等于相似比，面积的比等于相似比的平方。
①在测量河宽、物高及零件的内径等方面都有重要的应用。②同一时刻的物体的高度和它的影长成正比例。
① 定义及性质。② 作图：确定位似中心，找关键点，作关键点的对应点，连线。③ 平面直角坐标系中的位似变换及点的坐标变化规律。
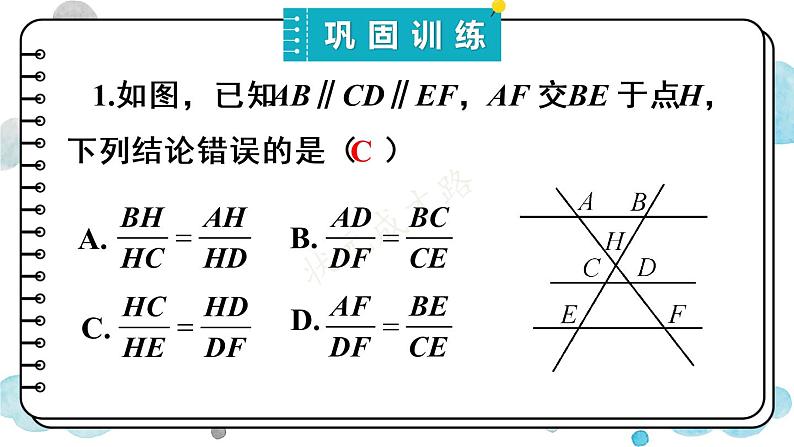
1.如图，已知AB∥CD∥EF，AF 交BE 于点H，下列结论错误的是（ ）
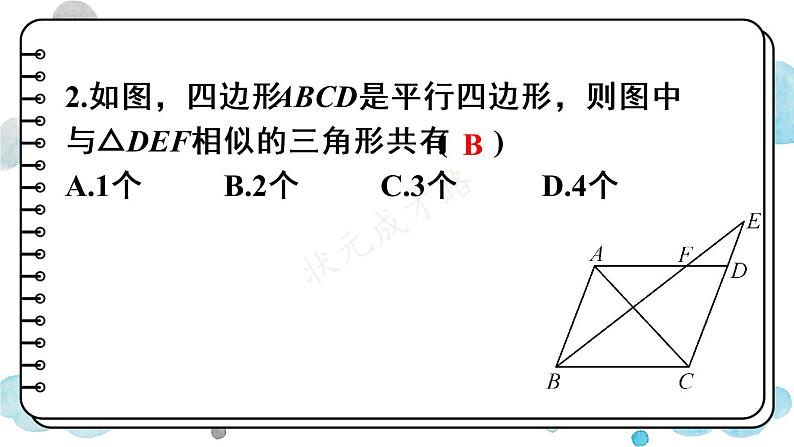
2.如图，四边形ABCD是平行四边形，则图中与△DEF相似的三角形共有( )A.1个 B.2个 C.3个 D.4个
3.如图，在大小为4×4的正方形网格中，是相似三角形的是（ ）
A.①和②B.②和③C.①和③D.②和④
4.如图, 小李打网球时, 球恰好打过网, 且落在离网4 m的位置上, 则球拍击球的高度h为( ) A.0.6 m B.1.2 m C.1.3 mD.1.4 m
5.在平面直角坐标系中，△ABC顶点A的坐标为(2，3)，若以原点O为位似中心，画△ABC的位似图形△A′B′C′，使△ABC与△A′B′C′的相似比等于2∶1，则点A′的坐标为 .
6.如图，AC⊥BC,∠ADC=90°，∠1=∠B,若AC=5，AB=6，求AD的长。
解：∵AC⊥BC, ∴∠ADC=∠ACB=90°, 又∵∠1=∠B, ∴△ADC∽△ACB. ∴ , 即 , 解得 AD= .
7.如图，△ABC内接于⊙O，AD是△ABC的边BC上的高，AE是⊙O的直径，连接BE，求证：AD·AE=AB·AC。证：∵AE是直径,AD⊥BC, ∴∠ABE=∠ADC=90°,又∵∠E=∠C,∴△ADC∽△ABE.∴ , 即 AD·AE=AB·AC.
1.从课后习题中选取；2.完成练习册本课时的习题.
1.如图，四边形EFGH相似于四边形KLMN，求∠E，∠G，∠N的度数以及x，y，z的值。
解：∠E=∠K=67°，∠G=∠M=107°，∠L=∠H=143°，∠N=360°-（67°+107°+143°）=43°.∵∴ x=14, y=15, z=25.
2.△ABC的三边长分别为5，12，13，与它相似的△DEF的最小边长为15，求△DEF的其他两条边长和周长。
解：∵ ，∴12×3=36,13×3=39,15+36+39=90.即其他两边的长为36和39.周长为90.
3.根据下列图中所注的条件，判断图中两个三角形是否相似，并求出x和y的值。
解：相似。图（1）由勾股定理求得x=4,y=10,∴ 且∠1=∠2，∴△FGH∽△JIH.图(2)中，∵∠KHG+∠KHJ=90°,∠KHG+∠GHF=90°,∴∠KHJ=∠GHF.又 ，∴△KJH∽△GFH，∴∠K＝x°=∠G=124°，∴x＝124，y=33.
4.李华要在报纸上刊登广告，一块10 cm×5 cm的长方形版面要付180元的广告费。如果他要把版面的边长扩大为原来的3倍，要付多少广告费（假设每平方厘米版面的广告费相同）？
解：扩大版面后的长方形与原版面相似，相似比为3∶1，面积的比为 付广告费180×9=1620（元）.
5.将如图所示的图形缩小，使得缩小前后对应线段的比为2∶1。
6.某同学的座位到黑板的距离是6 m，老师在黑板上要写多大的字，才能使这名同学看黑板上的字时，与他看相距30 cm的教科书上的字的感觉相同（教科书上的小四号字大小约为0.42 cm×0.42 cm）?
解：设黑板上的字的大小为xcm×xcm，则 ，x=8.4.∴黑板上的字应为8.4cm×8.4cm大.
7.如图，已知零件的外径为a，现用一个交叉卡钳（两条尺长AC和BD相等）测量零件的内孔直径AB。如果OA∶OC=OB∶OD=n，且量得CD=b，求AB以及零件厚度x。
解：∵OA∶OC=OB∶OD且∠AOB=∠COD；∴△AOB∽△COD,∴AB∶CD=OA∶OC=OB∶OD=n.∴AB=n·CD=nb. 厚度x=
8.如图，CD是⊙O的弦，AB是直径，且CD⊥AB，垂足为P，求证PC2=PA·PB。
证明：连接AC、BC.∵AB为⊙O的直径，∴∠ACB=90°，又CD⊥AB，∴∠APC=∠CPB=90°，∵∠PAC+∠ACP=90°,∠ACP+∠BCP=90°,∴∠PAC=∠BCP. ∴△APC∽△CPB.∴ 即PC 2=PA·PB.
9.如图，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED。你能在图中找出一对相似三角形，并说明相似的理由吗？
解：∵∠ADC=∠BEC=90°，∠C=∠C，∴△BEC∽△ADC.（答案不唯一）
10.如图，△ABC的三条边与△A′B′C′的三条边满足A′B′∥AB，B′C′∥BC，A′C′∥AC，且OB=3OB′。△ABC的面积与△A′B′C′的面积之间有什么关系？
解：由题可知△ABC与△A′B′C′位似，所以对应边及其对应高的比例均为3∶1，所以面积比为9∶1.
11.如图，△ABC是一块锐角三角形材料，边BC=120mm，高AD=80mm.把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB，AC上，这个正方形零件的边长是多少？
解：设正方形零件边长为x mm，AD与EF交于K，∵EF∥BC,∴△AEF∽△ABC，∴ ， 即解得x=48.因此这个正方形零件的边长是48mm.
12.如图，为了求出海岛上的山峰AB的高度，在D处和F处树立标杆CD和EF，标杆的高都是3丈，D，F两处相隔1000步（1丈=10尺，1步=6尺），并且AB，CD和EF在同一平面内。从标杆CD后退123步的G处，可以看到顶峰A和标杆顶端C在一条直线上；从标杆EF后退127步的H处，可以看到顶峰A和标杆顶端E在一条直线上。求山峰的高度AB及它和标杆CD的水平距离BD各是多少步？
（提示：连接EC并延长交AB于点K，用AK与常数的积表示KC和KE。）