山东省平原县2021-2022学年中考数学全真模拟试题含解析

这是一份山东省平原县2021-2022学年中考数学全真模拟试题含解析，共19页。
2021-2022中考数学模拟试卷
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题（共10小题，每小题3分，共30分）
1．若x＞y，则下列式子错误的是（ ）
A．x﹣3＞y﹣3 B．﹣3x＞﹣3y C．x+3＞y+3 D．
2．一个数和它的倒数相等，则这个数是（ ）
A．1 B．0 C．±1 D．±1和0
3．已知二次函数（m为常数）的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程的两实数根是
A．x1＝1，x2＝－1 B．x1＝1，x2＝2
C．x1＝1，x2＝0 D．x1＝1，x2＝3
4．如下字体的四个汉字中，是轴对称图形的是（ ）
A． B． C． D．
5．地球上的陆地面积约为149 000 000千米2，用科学记数法表示为 ( )
A．149×106千米2 B．14.9×107千米2
C．1.49×108千米2 D．0.149×109千2
6．已知3a﹣2b=1，则代数式5﹣6a+4b的值是（　　）
A．4 B．3 C．﹣1 D．﹣3
7．如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径圆弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=AB中，一定正确的是（ ）

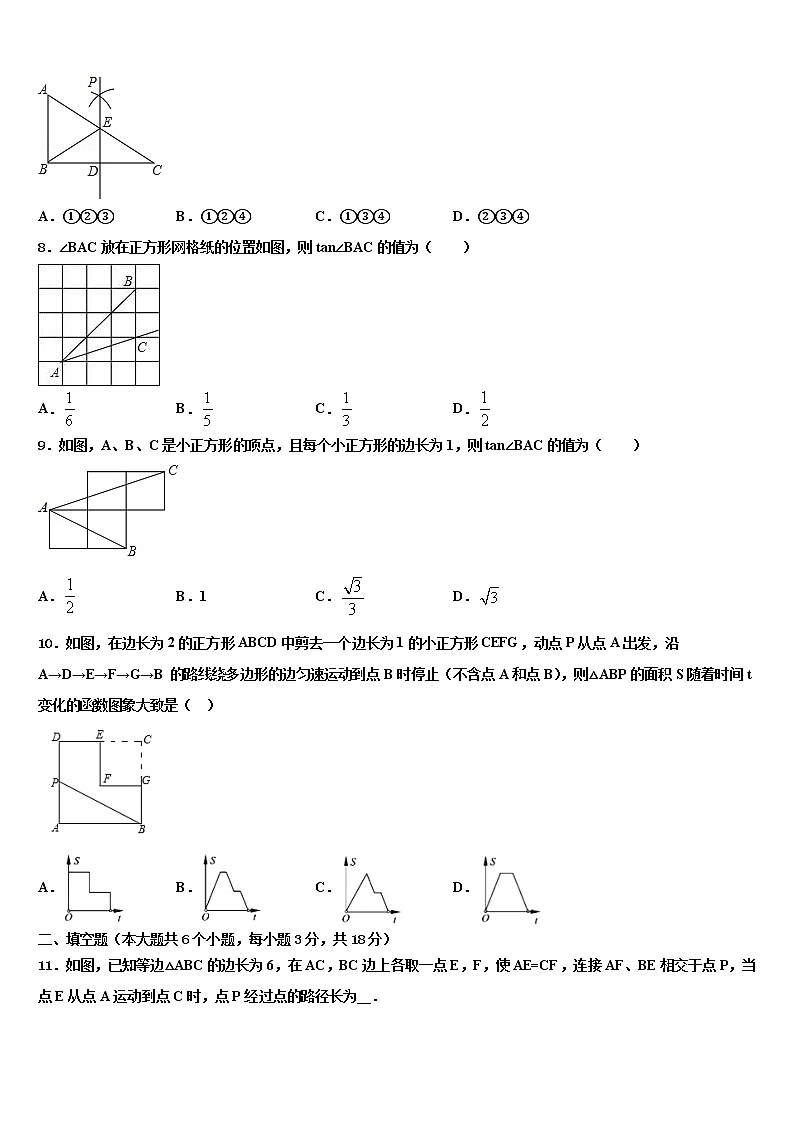
A．①②③ B．①②④ C．①③④ D．②③④
8．∠BAC放在正方形网格纸的位置如图，则tan∠BAC的值为（　　）

A． B． C． D．
9．如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为（　　）

A． B．1 C． D．
10．如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（ ）

A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．如图，已知等边△ABC的边长为6，在AC，BC边上各取一点E，F，使AE=CF，连接AF、BE相交于点P，当点E从点A运动到点C时，点P经过点的路径长为__．

12．如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是_____．

13．若点M（1，m）和点N（4，n）在直线y=﹣x+b上，则m___n（填＞、＜或=）
14．春节期间，《中国诗词大会)节目的播出深受观众喜爱，进一步激起了人们对古诗词的喜爱，现有以下四句古诗词：①锄禾日当午；②春眠不觉晓；③白日依山尽；④床前明月光.甲、乙两名同学从中各随机选取了一句写在纸上，则他们选取的诗句恰好相同的概率为________．
15．若y=，则x+y= ．
16．如图，点A、B、C是⊙O上的三点，且△AOB是正三角形，则∠ACB的度数是 。
三、解答题（共8题，共72分）
17．（8分）如图，四边形ABCD，AD∥BC，DC⊥BC于C点，AE⊥BD于E，且DB＝DA．求证：AE＝CD．

18．（8分）问题提出
（1）.如图 1，在四边形 ABCD 中，AB=BC，AD=CD=3, ∠BAD=∠BCD=90°，∠ADC=60°，则四边形 ABCD 的面积为 ＿；
问题探究
（2）.如图 2，在四边形 ABCD 中，∠BAD=∠BCD=90°，∠ABC=135°，AB=2 2，BC=3，在 AD、CD 上分别找一点 E、F， 使得△BEF 的周长最小，作出图像即可.

19．（8分）一次函数的图象经过点和点，求一次函数的解析式．
20．（8分）如图，在中，，垂足为D，点E在BC上，，垂足为，试判断DG与BC的位置关系，并说明理由．

21．（8分）如图，在正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边上的动点，且AE=BF=CG=DH．
（1）求证：△AEH≌△CGF；
（2）在点E、F、G、H运动过程中，判断直线EG是否经过某一个定点，如果是，请证明你的结论；如果不是，请说明理由

22．（10分）八年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类型，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．
类别
频数（人数）
频率
小说

0.5
戏剧
4

散文
10
0.25
其他
6

合计

1
根据图表提供的信息，解答下列问题：八年级一班有多少名学生？请补全频数分布表，并求出扇形统计图中“其他”类所占的百分比；在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组，请用画树状图或列表法的方法，求选取的2人恰好是乙和丙的概率．

23．（12分）矩形ABCD中，DE平分∠ADC交BC边于点E，P为DE上的一点（PE＜PD），PM⊥PD，PM交AD边于点M．
（1）若点F是边CD上一点，满足PF⊥PN，且点N位于AD边上，如图1所示．
求证：①PN=PF；②DF+DN=DP；
（2）如图2所示，当点F在CD边的延长线上时，仍然满足PF⊥PN，此时点N位于DA边的延长线上，如图2所示；试问DF，DN，DP有怎样的数量关系，并加以证明．

24．如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上且AB＝12cm
（1）若OB＝6cm．
①求点C的坐标；
②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值是多少cm．




参考答案

一、选择题（共10小题，每小题3分，共30分）
1、B
【解析】
根据不等式的性质在不等式两边加（或减）同一个数（或式子），不等号的方向不变；不等式两边乘（或除以）同一个正数，不等号的方向不变；不等式两边乘（或除以）同一个负数，不等号的方向改变即可得出答案：
A、不等式两边都减3，不等号的方向不变，正确；
B、乘以一个负数，不等号的方向改变，错误；
C、不等式两边都加3，不等号的方向不变，正确；
D、不等式两边都除以一个正数，不等号的方向不变，正确．
故选B．
2、C
【解析】
根据倒数的定义即可求解.
【详解】
的倒数等于它本身，故符合题意.
故选：.
【点睛】
主要考查倒数的概念及性质.倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数.
3、B
【解析】
试题分析：∵二次函数（m为常数）的图象与x轴的一个交点为(1，0)，
∴．∴．故选B．
4、A
【解析】
试题分析：根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此可知，A为轴对称图形．
故选A．
考点：轴对称图形
5、C
【解析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．
解：149 000 000=1.49×2千米1．
故选C．
把一个数写成a×10n的形式，叫做科学记数法，其中1≤|a|＜10，n为整数．因此不能写成149×106而应写成1.49×2．
6、B
【解析】
先变形，再整体代入，即可求出答案．
【详解】
∵3a﹣2b=1，
∴5﹣6a+4b=5﹣2（3a﹣2b）=5﹣2×1=3，
故选：B．
【点睛】
本题考查了求代数式的值，能够整体代入是解此题的关键．
7、B
【解析】
解：根据作图过程，利用线段垂直平分线的性质对各选项进行判断：
根据作图过程可知：PB=CP，
∵D为BC的中点，∴PD垂直平分BC，∴①ED⊥BC正确.
∵∠ABC=90°，∴PD∥AB.
∴E为AC的中点，∴EC=EA，∵EB=EC.
∴②∠A=∠EBA正确；③EB平分∠AED错误；④ED=AB正确.
∴正确的有①②④.
故选B．
考点：线段垂直平分线的性质.
8、D
【解析】
连接CD，再利用勾股定理分别计算出AD、AC、BD的长，然后再根据勾股定理逆定理证明∠ADC=90°，再利用三角函数定义可得答案．
【详解】
连接CD，如图：

，CD=，AC=
∵，∴∠ADC=90°，∴tan∠BAC==．
故选D．
【点睛】
本题主要考查了勾股定理，勾股定理逆定理，以及锐角三角函数定义，关键是证明∠ADC=90°．
9、B
【解析】
连接BC，由网格求出AB，BC，AC的长，利用勾股定理的逆定理得到△ABC为等腰直角三角形，即可求出所求．
【详解】
如图，连接BC，
由网格可得AB=BC=，AC=，即AB2+BC2=AC2，
∴△ABC为等腰直角三角形，
∴∠BAC=45°，
则tan∠BAC=1，
故选B．

【点睛】
本题考查了锐角三角函数的定义，解直角三角形，以及勾股定理，熟练掌握勾股定理是解本题的关键．
10、B
【解析】
解：当点P在AD上时，△ABP的底AB不变，高增大，所以△ABP的面积S随着时间t的增大而增大；
当点P在DE上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；
当点P在EF上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；
当点P在FG上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；
当点P在GB上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；
故选B．

二、填空题（本大题共6个小题，每小题3分，共18分）
11、π．
【解析】
由等边三角形的性质证明△AEB≌△CFA可以得出∠APB=120°，点P的路径是一段弧，由弧线长公式就可以得出结论．
【详解】
：∵△ABC为等边三角形，
∴AB=AC，∠C=∠CAB=60°，
又∵AE=CF，
在△ABE和△CAF中，
，
∴△ABE≌△CAF（SAS），
∴∠ABE=∠CAF．
又∵∠APE=∠BPF=∠ABP+∠BAP，
∴∠APE=∠BAP+∠CAF=60°．
∴∠APB=180°-∠APE=120°．
∴当AE=CF时，点P的路径是一段弧，且∠AOB=120°，
又∵AB=6，
∴OA=2，
点P的路径是l=，
故答案为．
【点睛】
本题考查了等边三角形的性质的运用，全等三角形的判定及性质的运用，弧线长公式的运用，解题的关键是证明三角形全等．
12、8﹣π
【解析】
分析：
如下图，过点D作DH⊥AE于点H，由此可得∠DHE=∠AOB=90°，由旋转的性质易得DE=EF=AB，OE=BO=2，OF=AO=3，∠DEF=∠FEO+∠DEH=90°，∠ABO=∠FEO，结合∠ABO+∠BAO=90°可得∠BAO=∠DEH，从而可证得△DEH≌△BAO，即可得到DH=BO=2，再由勾股定理求得AB的长，即可由S阴影=S扇形AOF+S△OEF+S△ADE-S扇形DEF即可求得阴影部分的面积.
详解：
如下图，过点D作DH⊥AE于点H，
∴∠DHE=∠AOB=90°，
∵OA=3，OB=2，
∴AB=，
由旋转的性质结合已知条件易得：DE=EF=AB= ，OE=BO=2，OF=AO=3，∠DEF=∠FEO+∠DEH=90°，∠ABO=∠FEO，
又∵∠ABO+∠BAO=90°，
∴∠BAO=∠DEH，
∴△DEH≌△BAO，
∴DH=BO=2，
∴S阴影=S扇形AOF+S△OEF+S△ADE-S扇形DEF
=
=.
故答案为：.

点睛：作出如图所示的辅助线，利用旋转的性质证得△DEH≌△BAO，由此得到DH=BO=2，从而将阴影部分的面积转化为：S阴影=S扇形AOF+S△OEF+S△ADE-S扇形DEF来计算是解答本题的关键.
13、＞
【解析】
根据一次函数的性质，k