山西省临汾市侯马市重点达标名校2021-2022学年中考数学最后冲刺浓缩精华卷含解析

这是一份山西省临汾市侯马市重点达标名校2021-2022学年中考数学最后冲刺浓缩精华卷含解析，共19页。试卷主要包含了考生要认真填写考场号和座位序号，下面的几何体中，主视图为圆的是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．当x=1时，代数式x3+x+m的值是7，则当x=﹣1时，这个代数式的值是（　　）
A．7 B．3 C．1 D．﹣7
2．关于x的不等式组无解，那么m的取值范围为( )
A．m≤－1 B．m<－1 C．－1 3．如图，AB与⊙O相切于点B，OA=2，∠OAB=30°，弦BC∥OA，则劣弧的长是（　　）

A． B． C． D．
4．下面的几何体中，主视图为圆的是（ ）
A． B． C． D．
5．如图，已知矩形ABCD中，BC＝2AB，点E在BC边上，连接DE、AE，若EA平分∠BED，则的值为（　　）

A． B． C． D．
6．设x1，x2是一元二次方程x2﹣2x﹣3=0的两根，则x12+x22=（ ）
A．6 B．8 C．10 D．12
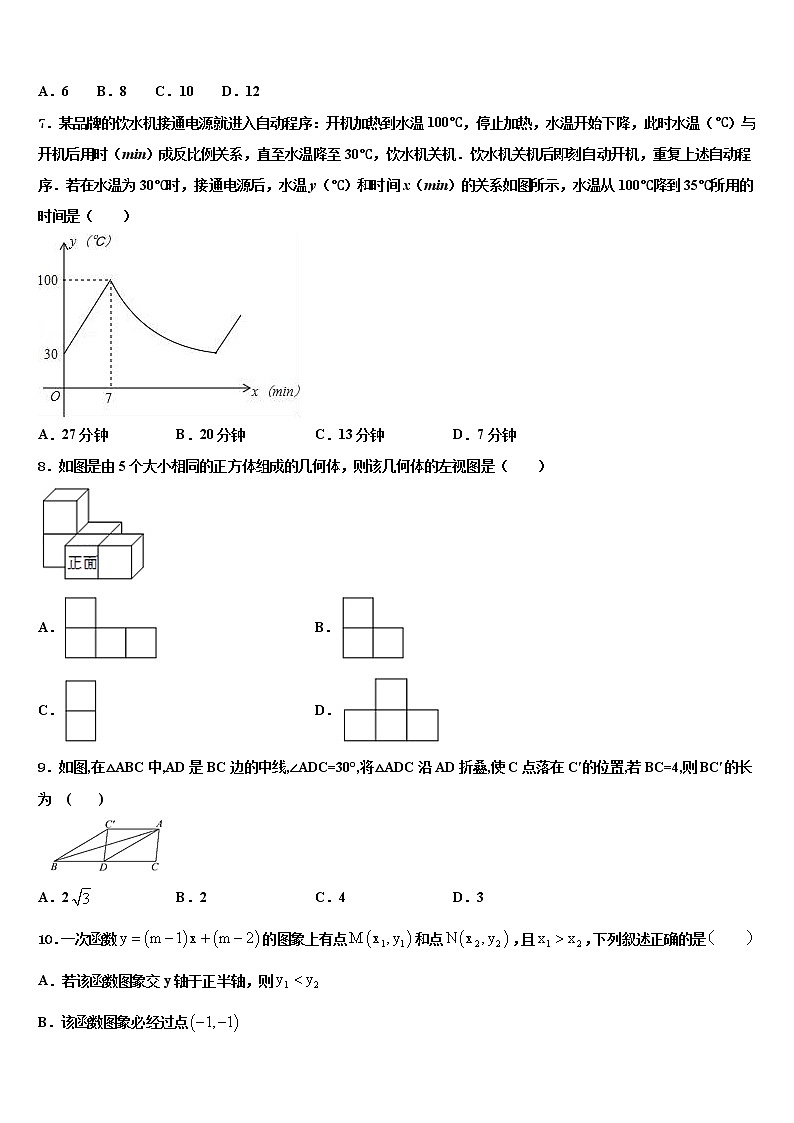
7．某品牌的饮水机接通电源就进入自动程序：开机加热到水温100℃，停止加热，水温开始下降，此时水温（℃）与开机后用时（min）成反比例关系，直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温y（℃）和时间x（min）的关系如图所示，水温从100℃降到35℃所用的时间是（　　）

A．27分钟 B．20分钟 C．13分钟 D．7分钟
8．如图是由5个大小相同的正方体组成的几何体，则该几何体的左视图是（　　）

A． B．
C． D．
9．如图,在△ABC中,AD是BC边的中线,∠ADC=30°,将△ADC沿AD折叠,使C点落在C′的位置,若BC=4,则BC′的长为　(　　)

A．2 B．2 C．4 D．3
10．一次函数的图象上有点和点，且，下列叙述正确的是　　
A．若该函数图象交y轴于正半轴，则
B．该函数图象必经过点
C．无论m为何值，该函数图象一定过第四象限
D．该函数图象向上平移一个单位后，会与x轴正半轴有交点
二、填空题（共7小题，每小题3分，满分21分）
11．若两个相似三角形的面积比为1∶4，则这两个相似三角形的周长比是__________．
12．一辆汽车在坡度为的斜坡上向上行驶130米，那么这辆汽车的高度上升了__________米.
13．工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合．过角尺顶点C的射线OC即是∠AOB的平分线．做法中用到全等三角形判定的依据是______．

14．如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，则大厅两层之间的高度为____米．（结果保留两个有效数字）（参考数据；sin31°=0.515，cos31°=0.857，tan31°=0.601）

15．因式分解：（a+1）（a﹣1）﹣2a+2＝_____．
16．如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，点B、E在第一象限，若点A的坐标为（1，0），则点E的坐标是______.

17．如图，在△ABC中，∠C＝90°，BC＝16 cm，AC＝12 cm，点P从点B出发，沿BC以2 cm/s的速度向点C移动，点Q从点C出发，以1 cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t＝__________时，△CPQ与△CBA相似．

三、解答题（共7小题，满分69分）
18．（10分）如图，∠BCD＝90°，且BC＝DC，直线PQ经过点D．设∠PDC＝α（45°＜α＜135°），BA⊥PQ于点A，将射线CA绕点C按逆时针方向旋转90°，与直线PQ交于点E．当α＝125°时，∠ABC＝　 　°；求证：AC＝CE；若△ABC的外心在其内部，直接写出α的取值范围．

19．（5分）某中学开展“汉字听写大赛”活动，为了解学生的参与情况，在该校随机抽取了四个班级学生进行调查，将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图，请根据图中的信息，解答下列问题：
（1）这四个班参与大赛的学生共__________人；
（2）请你补全两幅统计图；
（3）求图1中甲班所对应的扇形圆心角的度数；
（4）若四个班级的学生总数是160人，全校共2000人，请你估计全校的学生中参与这次活动的大约有多少人.
20．（8分）如图所示，点B、F、C、E在同一直线上，AB⊥BE，DE⊥BE，连接AC、DF，且AC=DF，BF=CE，求证：AB=DE．

21．（10分）先化简，再求值：÷（﹣x+1），其中x=sin30°+2﹣1+．
22．（10分）为了传承祖国的优秀传统文化，某校组织了一次“诗词大会”，小明和小丽同时参加，其中，有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗，其答案为“山重水复疑无路”.
(1)小明回答该问题时，仅对第二个字是选“重”还是选“穷”难以抉择，随机选择其中一个，则小明回答正确的概率是 ;
(2)小丽回答该问题时，对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择，若分别随机选择，请用列表或画树状图的方法求小丽回答正确的概率.
九宫格

23．（12分）已知.
（1）化简A；
（2）如果a,b 是方程的两个根，求A的值．
24．（14分）如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+1．求抛物线的表达式；在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．




参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、B
【解析】
因为当x=1时，代数式的值是7，所以1+1+m=7，所以m=5，当x=-1时，=-1-1+5=3，
故选B．
2、A
【解析】
【分析】先求出每一个不等式的解集，然后再根据不等式组无解得到有关m的不等式，就可以求出m的取值范围了.
【详解】，
解不等式①得：x 解不等式②得：x>-1，
由于原不等式组无解，所以m≤-1，
故选A.
【点睛】本题考查了一元一次不等式组无解问题，熟知一元一次不等式组解集的确定方法“大大取大，小小取小，大小小大中间找，大大小小无处找”是解题的关键.
3、B
【解析】
解：连接OB，OC．∵AB为圆O的切线，∴∠ABO=90°．在Rt△ABO中，OA=2，∠OAB=30°，∴OB=1，∠AOB=60°．∵BC∥OA，∴∠OBC=∠AOB=60°．又∵OB=OC，∴△BOC为等边三角形，∴∠BOC=60°，则劣弧BC的弧长为=π．故选B．

点睛：此题考查了切线的性质，含30度直角三角形的性质，以及弧长公式，熟练掌握切线的性质是解答本题的关键．
4、C
【解析】
试题解析：A、的主视图是矩形，故A不符合题意；
B、的主视图是正方形，故B不符合题意；
C、的主视图是圆，故C符合题意；
D、的主视图是三角形，故D不符合题意；
故选C．
考点：简单几何体的三视图．
5、C
【解析】
过点A作AF⊥DE于F，根据角平分线上的点到角的两边距离相等可得AF=AB，利用全等三角形的判定和性质以及矩形的性质解答即可．
【详解】
解：如图，过点A作AF⊥DE于F，

在矩形ABCD中，AB＝CD，
∵AE平分∠BED，
∴AF＝AB，
∵BC＝2AB，
∴BC＝2AF，
∴∠ADF＝30°，
在△AFD与△DCE中
∵∠C=∠AFD=90°,
∠ADF=∠DEC,
AF=DC,，
∴△AFD≌△DCE（AAS），
∴△CDE的面积＝△AFD的面积＝
∵矩形ABCD的面积＝AB•BC＝2AB2，
∴2△ABE的面积＝矩形ABCD的面积﹣2△CDE的面积＝（2﹣）AB2，
∴△ABE的面积＝,
∴，
故选：C．
【点睛】
本题考查了矩形的性质，角平分线上的点到角的两边距离相等的性质，以及全等三角形的判定与性质，关键是根据角平分线上的点到角的两边距离相等可得AF=AB．
6、C
【解析】
试题分析：根据根与系数的关系得到x1+x2=2，x1•x2=﹣3，再变形x12+x22得到（x1+x2）2﹣2x1•x2，然后利用代入计算即可．
解：∵一元二次方程x2﹣2x﹣3=0的两根是x1、x2，
∴x1+x2=2，x1•x2=﹣3，
∴x12+x22=（x1+x2）2﹣2x1•x2=22﹣2×（﹣3）=1．
故选C．
7、C
【解析】
先利用待定系数法求函数解析式，然后将y=35代入，从而求解．
【详解】
解：设反比例函数关系式为：，将（7，100）代入，得k=700，
∴，
将y=35代入，
解得；
∴水温从100℃降到35℃所用的时间是：20－7=13，
故选C．
【点睛】
本题考查反比例函数的应用，利用数形结合思想解题是关键．
8、B
【解析】
找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．
【详解】
解：从左面看易得下面一层有2个正方形，上面一层左边有1个正方形．
故选：B．
【点睛】
本题考查了三视图的知识，左视图是从物体的左面看得到的视图．
9、A
【解析】
连接CC′，
∵将△ADC沿AD折叠，使C点落在C′的位置，∠ADC=30°，
∴∠ADC′=∠ADC=30°，CD=C′D，
∴∠CDC′=∠ADC+∠ADC′=60°，
∴△DCC′是等边三角形，
∴∠DC′C=60°，
∵在△ABC中，AD是BC边的中线，
即BD=CD，
∴C′D=BD，
∴∠DBC′=∠DC′B=∠CDC′=30°，
∴∠BC′C=∠DC′B+∠DC′C=90°，
∵BC=4，
∴BC′=BC•cos∠DBC′=4×=2，
故选A.

【点睛】本题考查了折叠的性质、等边三角形的判定与性质、等腰三角形的性质、直角三角形的性质以及三角函数等知识，准确添加辅助线，掌握折叠前后图形的对应关系是解题的关键．
10、B
【解析】
利用一次函数的性质逐一进行判断后即可得到正确的结论．
【详解】
解：一次函数的图象与y轴的交点在y轴的正半轴上，则，，若，则，故A错误；
把代入得，，则该函数图象必经过点，故B正确；
当时，，，函数图象过一二三象限，不过第四象限，故C错误；
函数图象向上平移一个单位后，函数变为，所以当时，，故函数图象向上平移一个单位后，会与x轴负半轴有交点，故D错误，
故选B．
【点睛】
本题考查了一次函数图象上点的坐标特征、一次函数图象与几何变换，解题的关键是熟练掌握一次函数的性质，灵活应用这些知识解决问题，属于中考常考题型．

二、填空题（共7小题，每小题3分，满分21分）
11、　
【解析】
试题分析：∵两个相似三角形的面积比为1：4，∴这两个相似三角形的相似比为1：1，∴这两个相似三角形的周长比是1：1，故答案为1：1．
考点：相似三角形的性质．
12、50.
【解析】
根据坡度的定义可以求得AC、BC的比值，根据AC、BC的比值和AB的长度即可求得AC的值，即可解题.
【详解】
解：如图，米

，
设，则，
则，
解得，
故答案为：50.
【点睛】
本题考查了勾股定理在直角三角形中的运用，坡度的定义及直角三角形中三角函数值的计算，属于基础题.
13、SSS．
【解析】
由三边相等得△COM≌△CON，即由SSS判定三角全等．做题时要根据已知条件结合判定方法逐个验证．
【详解】
由图可知，CM=CN，又OM=ON，
∵在△MCO和△NCO中
，
∴△COM≌△CON（SSS），
∴∠AOC=∠BOC，
即OC是∠AOB的平分线．
故答案为：SSS．
【点睛】
本题考查了全等三角形的判定及性质．要熟练掌握确定三角形的判定方法，利用数学知识解决实际问题是一种重要的能力，要注意培养．
14、6.2
【解析】
根据题意和锐角三角函数可以求得BC的长，从而可以解答本题.
【详解】
解：在Rt△ABC中，
∵∠ACB=90°，
∴BC=AB•sin∠BAC=12×0.515≈6.2（米），
答：大厅两层之间的距离BC的长约为6.2米．
故答案为：6.2.
【点睛】
本题考查解直角三角形的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用锐角三角函数和数形结合的思想解答.
15、（a﹣1）1．
【解析】
提取公因式（a−1），进而分解因式得出答案．
【详解】
解：（a+1）（a﹣1）﹣1a+1
＝（a+1）（a﹣1）﹣1（a﹣1）
＝（a﹣1）（a+1﹣1）
＝（a﹣1）1．
故答案为：（a﹣1）1．
【点睛】
此题主要考查了提取公因式法分解因式，找出公因式是解题关键．
16、（，）
【解析】
由题意可得OA：OD=2：3，又由点A的坐标为（1，0），即可求得OD的长，又由正方形的性质，即可求得E点的坐标．
【详解】
解：∵正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为2：3，
∴OA：OD=2：3，
∵点A的坐标为（1，0），
即OA=1，
∴OD=，
∵四边形ODEF是正方形，
∴DE=OD=．
∴E点的坐标为：（，）．
故答案为：（，）．
【点睛】
此题考查了位似变换的性质与正方形的性质，注意理解位似变换与相似比的定义是解此题的关键．
17、4.8或
【解析】
根据题意可分两种情况，①当CP和CB是对应边时，△CPQ∽△CBA与②CP和CA是对应边时，△CPQ∽△CAB，根据相似三角形的性质分别求出时间t即可.
【详解】
①CP和CB是对应边时，△CPQ∽△CBA，
所以＝，
即＝，
解得t＝4.8；
②CP和CA是对应边时，△CPQ∽△CAB，
所以＝，
即＝，
解得t＝.
综上所述，当t＝4.8或时，△CPQ与△CBA相似．
【点睛】
此题主要考查相似三角形的性质，解题的关键是分情况讨论.

三、解答题（共7小题，满分69分）
18、（1）125；（2）详见解析；（3）45°＜α＜90°．
【解析】
（1）利用四边形内角和等于360度得：∠B+∠ADC＝180°，而∠ADC+∠EDC＝180°，即可求解；
（2）证明△ABC≌△EDC（AAS）即可求解；
（3）当∠ABC＝α＝90°时，△ABC的外心在其直角边上，∠ABC＝α＞90°时，△ABC的外心在其外部，即可求解．
【详解】
（1）在四边形BADC中，∠B+∠ADC＝360°﹣∠BAD﹣∠DCB＝180°，
而∠ADC+∠EDC＝180°，
∴∠ABC＝∠PDC＝α＝125°，
故答案为125；
（2）∠ECD+∠DCA＝90°，∠DCA+∠ACB＝90°，
∴∠ACB＝∠ECD，
又BC＝DC，由（1）知：∠ABC＝∠PDC，
∴△ABC≌△EDC（AAS），
∴AC＝CE；
（3）当∠ABC＝α＝90°时，△ABC的外心在其斜边上；∠ABC＝α＞90°时，△ABC的外心在其外部，而45°＜α＜135°，故：45°＜α＜90°．
【点睛】
本题考查圆的综合运用，解题的关键是掌握三角形全等的判定和性质（AAS）、三角形外心．
19、（1）100；（2）见解析；（3）108°；（4）1250.
【解析】
试题分析：（1）根据乙班参赛30人，所占比为20%，即可求出这四个班总人数；
（2）根据丁班参赛35人，总人数是100，即可求出丁班所占的百分比，再用整体1减去其它所占的百分比，即可得出丙所占的百分比，再乘以参赛得总人数，即可得出丙班参赛得人数，从而补全统计图；
（3）根据甲班级所占的百分比，再乘以360°，即可得出答案；
（4）根据样本估计总体，可得答案．
试题解析：（1）这四个班参与大赛的学生数是：
30÷30%=100（人）；
故答案为100；
（2）丁所占的百分比是：×100%=35%，
丙所占的百分比是：1﹣30%﹣20%﹣35%=15%，
则丙班得人数是：100×15%=15（人）；
如图：

（3）甲班级所对应的扇形圆心角的度数是：30%×360°=108°；
（4）根据题意得：2000×=1250（人）．
答：全校的学生中参与这次活动的大约有1250人．
考点：条形统计图；扇形统计图；样本估计总体.
20、证明见解析
【解析】
试题分析：证明三角形△ABC△DEF,可得＝.
试题解析：
证明：∵＝，
∴BC=EF,
∵⊥，⊥，
∴∠B=∠E=90°，AC=DF,
∴△ABC△DEF,
∴AB=DE.
21、-5
【解析】
根据分式的运算法则以及实数的运算法则即可求出答案．
【详解】
当x=sin30°+2﹣1+时，
∴x=++2=3，
原式=÷==﹣5.
【点睛】
本题考查分式的运算法则，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
22、（1）；（2）
【解析】
试题分析：（1）利用概率公式直接计算即可；
（2）画出树状图得到所有可能的结果，再找到回答正确的数目即可求出小丽回答正确的概率．
试题解析：
（1）∵对第二个字是选“重”还是选“穷”难以抉择，∴若随机选择其中一个正确的概率=，故答案为；
（2）画树形图得：

由树状图可知共有4种可能结果，其中正确的有1种，所以小丽回答正确的概率=．
考点：列表法与树状图法；概率公式．
23、（1）；（2）-.
【解析】
（1）先通分，再根据同分母的分式相加减求出即可；
（2）根据根与系数的关系即可得出结论．
【详解】
（1）A=﹣
=
=；
（2）∵a，b 是方程的两个根，∴a+b=4，ab=－12，∴．
【点睛】
本题考查了分式的加减和根与系数的关系，能正确根据分式的运算法则进行化简是解答此题的关键．
24、（1）y=﹣x2+2x+1；（2）P ( ,)；（1）当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．
【解析】
（1）先求得点B和点C的坐标，然后将点B和点C的坐标代入抛物线的解析式得到关于b、c的方程，从而可求得b、c的值；（2）作点O关于BC的对称点O′，则O′（1，1），则OP+AP的最小值为AO′的长，然后求得AO′的解析式，最后可求得点P的坐标；（1）先求得点D的坐标，然后求得CD、BC、BD的长，依据勾股定理的逆定理证明△BCD为直角三角形，然后分为△AQC∽△DCB和△ACQ∽△DCB两种情况求解即可．
【详解】
（1）把x=0代入y=﹣x+1，得：y=1，
∴C（0，1）．
把y=0代入y=﹣x+1得：x=1，
∴B（1，0），A（﹣1，0）.
将C（0，1）、B（1，0）代入y=﹣x2+bx+c得： ，解得b=2，c=1．
∴抛物线的解析式为y=﹣x2+2x+1．
（2）如图所示：作点O关于BC的对称点O′，则O′（1，1）．

∵O′与O关于BC对称，
∴PO=PO′．
∴OP+AP=O′P+AP≤AO′．
∴OP+AP的最小值=O′A==2．
O′A的方程为y=
P点满足解得：
所以P ( ,)
（1）y=﹣x2+2x+1=﹣（x﹣1）2+4，
∴D（1，4）．
又∵C（0，1，B（1，0），
∴CD=，BC=1，DB=2．
∴CD2+CB2=BD2，
∴∠DCB=90°．
∵A（﹣1，0），C（0，1），
∴OA=1，CO=1．
∴．
又∵∠AOC=DCB=90°，
∴△AOC∽△DCB．
∴当Q的坐标为（0，0）时，△AQC∽△DCB．
如图所示：连接AC，过点C作CQ⊥AC，交x轴与点Q．

∵△ACQ为直角三角形，CO⊥AQ，
∴△ACQ∽△AOC．
又∵△AOC∽△DCB，
∴△ACQ∽△DCB．
∴，即，解得：AQ=3．
∴Q（9，0）．
综上所述，当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．
【点睛】
本题考查了二次函数的综合应用，解题的关键是掌握待定系数法求二次函数的解析式、轴对称图形的性质、相似三角形的性质和判定，分类讨论的思想．