

山西省大同市云冈区2021-2022学年中考数学模拟预测试卷含解析
展开
这是一份山西省大同市云冈区2021-2022学年中考数学模拟预测试卷含解析,共23页。试卷主要包含了已知点A等内容,欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
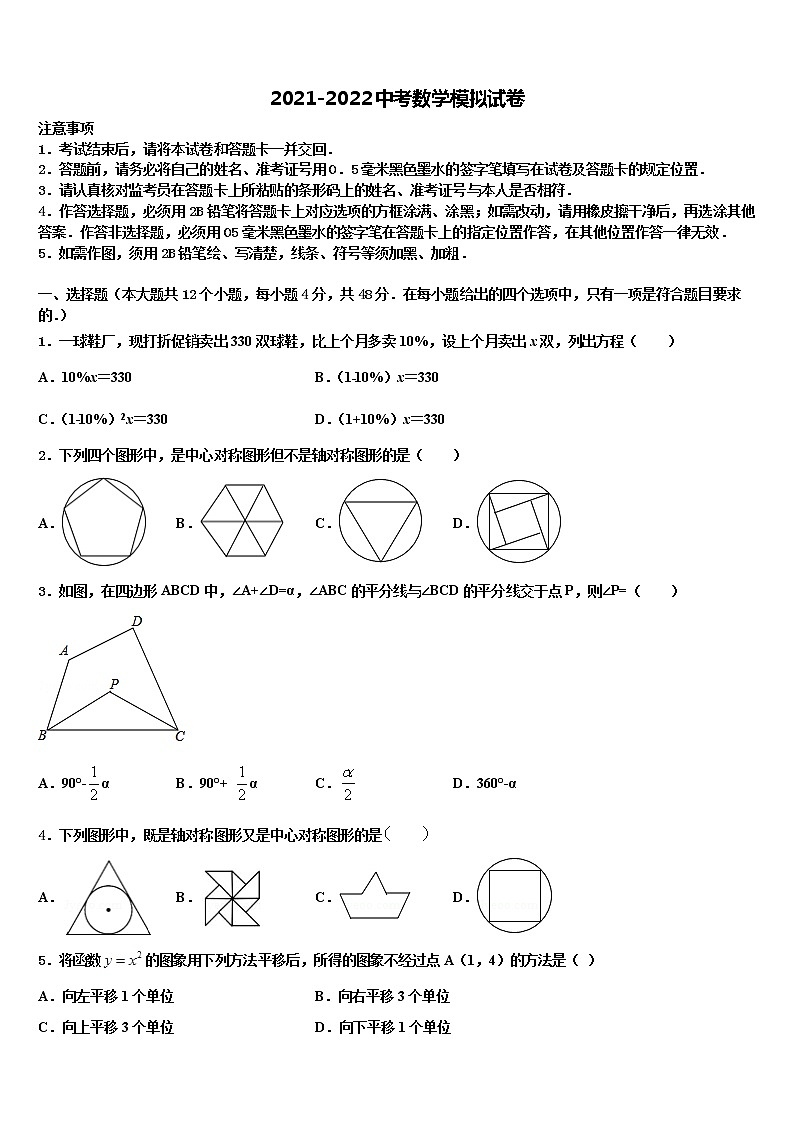
1.一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x双,列出方程( )
A.10%x=330 B.(1﹣10%)x=330
C.(1﹣10%)2x=330 D.(1+10%)x=330
2.下列四个图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
3.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°-α B.90°+ α C. D.360°-α
4.下列图形中,既是轴对称图形又是中心对称图形的是
A. B. C. D.
5.将函数的图象用下列方法平移后,所得的图象不经过点A(1,4)的方法是( )
A.向左平移1个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移1个单位
6.如图,△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,CD=3,BD=4,则⊙O的直径等于( )
A.5 B. C. D.7
7.已知点A(1﹣2x,x﹣1)在第二象限,则x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
8.已知关于x的一元二次方程有实数根,则m的取值范围是( )
A. B. C. D.
9.如图,矩形中,,,以为圆心,为半径画弧,交于点,以为圆心,为半径画弧,交于点,则的长为( )
A.3 B.4 C. D.5
10.如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
A.13 B.17 C.18 D.25
11.如图,△ABC中,∠ACB=90°,∠A=30°,AB=1.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
12.一个几何体的三视图如图所示,这个几何体是( )
A.棱柱 B.正方形 C.圆柱 D.圆锥
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13.有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么是方程N的一个根.
14.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中方程术是重要的数学成就.书中有一个方程问题:今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?意思是:今有美酒一斗,价格是50钱;普通酒一斗,价格是10钱.现在买两种酒2斗共付30钱,问买美酒、普通酒各多少?设买美酒x斗,买普通酒y斗,则可列方程组为______________.
15.如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD,则∠BDC的度数为_____度.
16.如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,则扇形OAB周长等于_____.(结果保留根号及π).
17.用黑白两种颜色的正六边形地面砖按如图所示的规律,拼成若干图案:
第4个图案有白色地面砖______块;第n个图案有白色地面砖______块.
18.一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是______.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19.(6分)如图,在△ABC中,CD⊥AB于点D,tanA=2cos∠BCD,
(1)求证:BC=2AD;
(2)若cosB=,AB=10,求CD的长.
20.(6分)我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托,折回索子却量竿,却比竿子短一托”其大意为:现有一根竿和一根绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.求绳索长和竿长.
21.(6分)如图,点A、B在⊙O上,点O是⊙O的圆心,请你只用无刻度的直尺,分别画出图①和图②中∠A的余角.
(1)图①中,点C在⊙O上;
(2)图②中,点C在⊙O内;
22.(8分)如图,∠AOB=90°,反比例函数y=﹣(x<0)的图象过点A(﹣1,a),反比例函数y=(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=于另一点C,求△OBC的面积.
23.(8分)某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分):整理、分析过程如下,请补充完整.
(1)按如下分数段整理、描述这两组数据:
成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
______
______
______
______
______
______
乙
1
1
4
2
1
1
(2)两组数据的极差、平均数、中位数、众数、方差如下表所示:
学生
极差
平均数
中位数
众数
方差
甲
______
83.7
______
86
13.21
乙
24
83.7
82
______
46.21
(3)若从甲、乙两人中选择一人参加知识竞赛,你会选______(填“甲”或“乙),理由为______.
24.(10分)已知:如图,在Rt△ABO中,∠B=90°,∠OAB=10°,OA=1.以点O为原点,斜边OA所在直线为x轴,建立平面直角坐标系,以点P(4,0)为圆心,PA长为半径画圆,⊙P与x轴的另一交点为N,点M在⊙P上,且满足∠MPN=60°.⊙P以每秒1个单位长度的速度沿x轴向左运动,设运动时间为ts,解答下列问题:
(发现)(1)的长度为多少;
(2)当t=2s时,求扇形MPN(阴影部分)与Rt△ABO重叠部分的面积.
(探究)当⊙P和△ABO的边所在的直线相切时,求点P的坐标.
(拓展)当与Rt△ABO的边有两个交点时,请你直接写出t的取值范围.
25.(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
求证:△ADF∽△DEC;若AB=8,AD=6,AF=4,求AE的长.
26.(12分)某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.
27.(12分)如图,在中,,是边上的高线,平分交于点,经过,两点的交于点,交于点,为的直径.
(1)求证:是的切线;
(2)当,时,求的半径.
参考答案
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、D
【解析】
解:设上个月卖出x双,根据题意得:(1+10%)x=1.故选D.
2、D
【解析】
根据轴对称图形与中心对称图形的概念判断即可.
【详解】
A、是轴对称图形,不是中心对称图形;
B、是轴对称图形,不是中心对称图形;
C、是轴对称图形,不是中心对称图形;
D、不是轴对称图形,是中心对称图形.
故选D.
【点睛】
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
3、C
【解析】
试题分析:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,
则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.
故选C.
考点:1.多边形内角与外角2.三角形内角和定理.
4、D
【解析】
根据轴对称图形和中心对称图形的定义逐项识别即可,在平面内,把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【详解】
解:A. 是轴对称图形,但不是中心对称图形,故不符合题意;
B. 不是轴对称图形,是中心对称图形,故不符合题意;
C. 是轴对称图形,但不是中心对称图形,故不符合题意;
D. 既是轴对称图形又是中心对称图形,故符合题意.
故选D.
【点睛】
本题考查了轴对称图形和中心对称图形的识别,熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键.
5、D
【解析】
A.平移后,得y=(x+1)2,图象经过A点,故A不符合题意;
B.平移后,得y=(x−3)2,图象经过A点,故B不符合题意;
C.平移后,得y=x2+3,图象经过A点,故C不符合题意;
D.平移后,得y=x2−1图象不经过A点,故D符合题意;
故选D.
6、A
【解析】
连接AO并延长到E,连接BE.设AE=2R,则∠ABE=90°,∠AEB=∠ACB,∠ADC=90°,利用勾股定理求得AD=,, 再证明Rt△ABE∽Rt△ADC,得到 ,即2R= = .
【详解】
解:如图,
连接AO并延长到E,连接BE.设AE=2R,则
∠ABE=90°,∠AEB=∠ACB;
∵AD⊥BC于D点,AC=5,DC=3,
∴∠ADC=90°,
∴AD=,
∴
在Rt△ABE与Rt△ADC中,
∠ABE=∠ADC=90°,∠AEB=∠ACB,
∴Rt△ABE∽Rt△ADC,
∴,
即2R= = ;
∴⊙O的直径等于.
故答案选:A.
【点睛】
本题主要考查了圆周角定理、勾股定理,解题的关键是掌握辅助线的作法.
7、B
【解析】
先分别求出每一个不等式的解集,再根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【详解】
解:根据题意,得: ,
解不等式①,得:x>,
解不等式②,得:x>1,
∴不等式组的解集为x>1,
故选:B.
【点睛】
本题主要考查解一元一次不等式组,关键要掌握解一元一次不等式的方法,牢记确定不等式组解集方法.
8、C
【解析】
解:∵关于x的一元二次方程有实数根,
∴△==,
解得m≥1,
故选C.
【点睛】
本题考查一元二次方程根的判别式.
9、B
【解析】
连接DF,在中,利用勾股定理求出CF的长度,则EF的长度可求.
【详解】
连接DF,
∵四边形ABCD是矩形
∴
在中,
故选:B.
【点睛】
本题主要考查勾股定理,掌握勾股定理的内容是解题的关键.
10、C
【解析】
在Rt△ABC中,∠ACB=90°,BC=12,AC=5,根据勾股定理求得AB=13.根据题意可知,EF为线段AB的垂直平分线,在Rt△ABC中,根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB,所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.
11、D
【解析】
解:当点Q在AC上时,∵∠A=30°,AP=x,∴PQ=xtan30°=,∴y=×AP×PQ=×x×=x2;
当点Q在BC上时,如下图所示:
∵AP=x,AB=1,∠A=30°,∴BP=1﹣x,∠B=60°,∴PQ=BP•tan60°=(1﹣x),∴ =AP•PQ= = ,∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.故选D.
点睛:本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.
12、C
【解析】试题解析:根据主视图和左视图为矩形可判断出该几何体是柱体,
根据俯视图是圆可判断出该几何体为圆柱.
故选C.
二、填空题:(本大题共6个小题,每小题4分,共24分.)
13、①②④
【解析】
试题解析:①在方程ax2+bx+c=0中△=b2-4ac,在方程cx2+bx+a=0中△=b2-4ac,
∴如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根,正确;
②∵和符号相同,和符号也相同,
∴如果方程M有两根符号相同,那么方程N的两根符号也相同,正确;
③、M-N得:(a-c)x2+c-a=0,即(a-c)x2=a-c,
∵a≠c,
∴x2=1,解得:x=±1,错误;
④∵5是方程M的一个根,
∴25a+5b+c=0,
∴a+b+c=0,
∴是方程N的一个根,正确.
故正确的是①②④.
14、
【解析】
设买美酒x斗,买普通酒y斗,根据“美酒一斗的价格是50钱、买两种酒2斗共付30钱”列出方程组.
【详解】
依题意得:.
故答案为.
【点睛】
考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
15、1
【解析】
根据△EBD由△ABC旋转而成,得到△ABC≌△EBD,则BC=BD,∠EBD=∠ABC=30°,则有∠BDC=∠BCD,∠DBC=180﹣30°=10°,化简计算即可得出.
【详解】
解:∵△EBD由△ABC旋转而成,
∴△ABC≌△EBD,
∴BC=BD,∠EBD=∠ABC=30°,
∴∠BDC=∠BCD,∠DBC=180﹣30°=10°,
∴;
故答案为:1.
【点睛】
此题考查旋转的性质,即图形旋转后与原图形全等.
16、π+4
【解析】
根据正方形的性质,得扇形所在的圆心角是90°,扇形的半径是2.
解:根据图形中正方形的性质,得
∠AOB=90°,OA=OB=2.
∴扇形OAB的弧长等于π.
17、18块 (4n+2)块.
【解析】
由已知图形可以发现:前三个图形中白色地砖的块数分别为:6,10,14,所以可以发现每一个图形都比它前一个图形多4个白色地砖,所以可以得到第n个图案有白色地面砖(4n+2)块.
【详解】
解:第1个图有白色块4+2,第2图有4×2+2,第3个图有4×3+2,
所以第4个图应该有4×4+2=18块,
第n个图应该有(4n+2)块.
【点睛】
此题考查了平面图形,主要培养学生的观察能力和空间想象能力.
18、7
【解析】
根据多边形内角和公式得:(n-2) .得:
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.
19、(1)证明见解析;(2)CD=2.
【解析】
(1)根据三角函数的概念可知tanA=,cos∠BCD=,根据tanA=2cos∠BCD即可得结论;(2)由∠B的余弦值和(1)的结论即可求得BD,利用勾股定理求得CD即可.
【详解】
(1)∵tanA=,cos∠BCD=,tanA=2cos∠BCD,
∴=2·,
∴BC=2AD.
(2)∵cosB==,BC=2AD,
∴=.
∵AB=10,∴AD=×10=4,BD=10-4=6,
∴BC=8,∴CD==2.
【点睛】
本题考查了直角三角形中的有关问题,主要考查了勾股定理,三角函数的有关计算.熟练掌握三角函数的概念是解题关键.
20、绳索长为20尺,竿长为15尺.
【解析】
设索长为x尺,竿子长为y尺,根据“索比竿子长一托,对折索子来量竿,却比竿子短一托”,即可得出关于x、y的二元一次方程组,解之即可得出结论.
【详解】
设绳索长、竿长分别为尺,尺,
依题意得:
解得:,.
答:绳索长为20尺,竿长为15尺.
【点睛】
本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
21、图形见解析
【解析】试题分析:(1)根据同弧所对的圆周角相等和直径所对的圆周角为直角画图即可;(2)延长AC交⊙O于点E ,利用(1)的方法画图即可.
试题解析:
如图①∠DBC就是所求的角;
如图②∠FBE就是所求的角
22、(1)a=2,k=8(2) =1.
【解析】
分析:(1)把A(-1,a)代入反比例函数得到A(-1,2),过A作AE⊥x轴于E,BF⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;
(2)求的直线AO的解析式为y=-2x,设直线MN的解析式为y=-2x+b,得到直线MN的解析式为y=-2x+10,解方程组得到C(1,8),于是得到结论.
详解:(1)∵反比例函数y=﹣(x<0)的图象过点A(﹣1,a),
∴a=﹣=2,
∴A(﹣1,2),
过A作AE⊥x轴于E,BF⊥⊥x轴于F,
∴AE=2,OE=1,
∵AB∥x轴,
∴BF=2,
∵∠AOB=90°,
∴∠EAO+∠AOE=∠AOE+∠BOF=90°,
∴∠EAO=∠BOF,
∴△AEO∽△OFB,
∴,
∴OF=4,
∴B(4,2),
∴k=4×2=8;
(2)∵直线OA过A(﹣1,2),
∴直线AO的解析式为y=﹣2x,
∵MN∥OA,
∴设直线MN的解析式为y=﹣2x+b,
∴2=﹣2×4+b,
∴b=10,
∴直线MN的解析式为y=﹣2x+10,
∵直线MN交x轴于点M,交y轴于点N,
∴M(5,0),N(0,10),
解得,,
∴C(1,8),
∴△OBC的面积=S△OMN﹣S△OCN﹣S△OBM=5×10﹣×10×1﹣×5×2=1.
点睛:本题考查了一次函数图象上点的坐标特征,反比例函数与一次函数交点问题,相似三角形的判定和性质,求函数的解析式,三角形的面积的计算,正确的作出辅助线是解题的关键.
23、(1)0,1,4,5,0,0;(2)14,84.5,1;(3)甲,理由见解析
【解析】
(1)根据折线统计图数字进行填表即可;
(2)根据稽查,中位数,众数的计算方法,求得甲成绩的极差,中位数,乙成绩的极差,众数即可;
(3)可分别从平均数、方差、极差三方面进行比较.
【详解】
(1)由图可知:甲的成绩为:75,84,89,82,86,1,86,83,85,86,
∴70⩽x⩽74无,共0个;
75⩽x⩽79之间有75,共1个;
80⩽x⩽84之间有84,82,1,83,共4个;
85⩽x⩽89之间有89,86,86,85,86,共5个;
90⩽x⩽94之间和95⩽x⩽100无,共0个.
故答案为0;1;4;5;0;0;
(2)由图可知:甲的最高分为89分,最低分为75分,极差为89−75=14分;
∵甲的成绩为从低到高排列为:75,1,82,83,84,85,86,86,86,89,
∴中位数为(84+85)=84.5;
∵乙的成绩为从低到高排列为:72,76,1,1,1,83,87,89,91,96,
1出现3次,乙成绩的众数为1.
故答案为14;84.5;1;
(3)甲,理由:两人的平均数相同且甲的方差小于乙,说明甲成绩稳定;两人的平均数相同且甲的极差小于乙,说明甲成绩变化范围小.
或:乙,理由:在90≤x≤100的分数段中,乙的次数大于甲.(答案不唯一,理由须支撑推断结论)
故答案为:甲,两人的平均数相同且甲的方差小于乙,说明甲成绩稳定.
【点睛】
此题考查折线统计图,统计表,平均数,中位数,众数,方差,极差,解题关键在于掌握运算法则以及会用这些知识来评价这组数据.
24、【发现】(3)的长度为;(2)重叠部分的面积为;【探究】:点P的坐标为;或或;【拓展】t的取值范围是或,理由见解析.
【解析】
发现:(3)先确定出扇形半径,进而用弧长公式即可得出结论;
(2)先求出PA=3,进而求出PQ,即可用面积公式得出结论;
探究:分圆和直线AB和直线OB相切,利用三角函数即可得出结论;
拓展:先找出和直角三角形的两边有两个交点时的分界点,即可得出结论.
【详解】
[发现]
(3)∵P(2,0),∴OP=2.
∵OA=3,∴AP=3,∴的长度为.
故答案为;
(2)设⊙P半径为r,则有r=2﹣3=3,当t=2时,如图3,点N与点A重合,∴PA=r=3,设MP与AB相交于点Q.在Rt△ABO中,∵∠OAB=30°,∠MPN=60°.
∵∠PQA=90°,∴PQPA,∴AQ=AP×cos30°,∴S重叠部分=S△APQPQ×AQ.
即重叠部分的面积为.
[探究]
①如图2,当⊙P与直线AB相切于点C时,连接PC,则有PC⊥AB,PC=r=3.
∵∠OAB=30°,∴AP=2,∴OP=OA﹣AP=3﹣2=3;
∴点P的坐标为(3,0);
②如图3,当⊙P与直线OB相切于点D时,连接PD,则有PD⊥OB,PD=r=3,∴PD∥AB,∴∠OPD=∠OAB=30°,∴cos∠OPD,∴OP,∴点P的坐标为(,0);
③如图2,当⊙P与直线OB相切于点E时,连接PE,则有PE⊥OB,同②可得:OP;
∴点P的坐标为(,0);
[拓展]
t的取值范围是2<t≤3,2≤t<4,理由:
如图4,当点N运动到与点A重合时,与Rt△ABO的边有一个公共点,此时t=2;
当t>2,直到⊙P运动到与AB相切时,由探究①得:OP=3,∴t3,与Rt△ABO的边有两个公共点,∴2<t≤3.
如图6,当⊙P运动到PM与OB重合时,与Rt△ABO的边有两个公共点,此时t=2;
直到⊙P运动到点N与点O重合时,与Rt△ABO的边有一个公共点,此时t=4;
∴2≤t<4,即:t的取值范围是2<t≤3,2≤t<4.
【点睛】
本题是圆的综合题,主要考查了弧长公式,切线的性质,锐角三角函数,三角形面积公式,作出图形是解答本题的关键.
25、(1)见解析(2)6
【解析】
(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC.
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在在Rt△ADE中,利用勾股定理求出线段AE的长度.
【详解】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC
∴∠C+∠B=110°,∠ADF=∠DEC
∵∠AFD+∠AFE=110°,∠AFE=∠B,
∴∠AFD=∠C
在△ADF与△DEC中,∵∠AFD=∠C,∠ADF=∠DEC,
∴△ADF∽△DEC
(2)∵四边形ABCD是平行四边形,
∴CD=AB=1.
由(1)知△ADF∽△DEC,
∴,
∴
在Rt△ADE中,由勾股定理得:
26、(1)P=t+2;(2)①当0<t≤8时,w=240;当8<t≤12时,w=2t2+12t+16;当12<t≤24时,w=﹣t2+42t+88;②此范围所对应的月销售量P的最小值为12吨,最大值为19吨.
【解析】
分析:(1)设8<t≤24时,P=kt+b,将A(8,10)、B(24,26)代入求解可得P=t+2;
(2)①分0<t≤8、8<t≤12和12<t≤24三种情况,根据月毛利润=月销量×每吨的毛利润可得函数解析式;
②求出8<t≤12和12<t≤24时,月毛利润w在满足336≤w≤513条件下t的取值范围,再根据一次函数的性质可得P的最大值与最小值,二者综合可得答案.
详解:(1)设8<t≤24时,P=kt+b,
将A(8,10)、B(24,26)代入,得:
,
解得:,
∴P=t+2;
(2)①当0<t≤8时,w=(2t+8)×=240;
当8<t≤12时,w=(2t+8)(t+2)=2t2+12t+16;
当12<t≤24时,w=(-t+44)(t+2)=-t2+42t+88;
②当8<t≤12时,w=2t2+12t+16=2(t+3)2-2,
∴8<t≤12时,w随t的增大而增大,
当2(t+3)2-2=336时,解题t=10或t=-16(舍),
当t=12时,w取得最大值,最大值为448,
此时月销量P=t+2在t=10时取得最小值12,在t=12时取得最大值14;
当12<t≤24时,w=-t2+42t+88=-(t-21)2+529,
当t=12时,w取得最小值448,
由-(t-21)2+529=513得t=17或t=25,
∴当12<t≤17时,448<w≤513,
此时P=t+2的最小值为14,最大值为19;
综上,此范围所对应的月销售量P的最小值为12吨,最大值为19吨.
点睛:本题主要考查二次函数的应用,掌握待定系数法求函数解析式及根据相等关系列出分段函数的解析式是解题的前提,利用二次函数的性质求得336≤w≤513所对应的t的取值范围是解题的关键.
27、(1)见解析;(2)的半径是.
【解析】
(1)连结,易证,由于是边上的高线,从而可知,所以是的切线.
(2)由于,从而可知,由,可知:,易证,所以,再证明,所以,从而可求出.
【详解】
解:(1)连结.
∵平分,
∴,又,
∴,
∴,
∵是边上的高线,
∴,
∴,
∴是的切线.
(2)∵,
∴,,
∴是中点,
∴,
∵,
∴,
∵,,
∴,
∴,
又∵,
∴,
在中,
,
∴,
∴,
,
而,
∴,
∴,
∴的半径是.
【点睛】
本题考查圆的综合问题,涉及锐角三角函数,相似三角形的判定与性质,等腰三角形的性质等知识,综合程度较高,需要学生综合运用知识的能力.
相关试卷
这是一份2023-2024学年山西省大同市云冈区数学九上期末经典模拟试题含答案,共8页。试卷主要包含了若x=2y,则的值为,设A,方程的解是等内容,欢迎下载使用。
这是一份山西省大同市云冈区2022-2023学年七年级上学期期末模拟测试数学试卷(含解析),共14页。试卷主要包含了选择题等内容,欢迎下载使用。
这是一份山西省大同市云冈区2022-2023学年八年级上学期期末模拟测试数学试卷(含解析,答案不全),共15页。试卷主要包含了选择题等内容,欢迎下载使用。










