北师大版八年级上册1 探索勾股定理教学演示课件ppt

这是一份北师大版八年级上册1 探索勾股定理教学演示课件ppt，共18页。PPT课件主要包含了导入新课，探究新知，SA＋SB＝SC，你发现了吗，应用举例，解由题意，课堂小结，随堂练习等内容，欢迎下载使用。

我们知道，任意三角形的三条边必须满足定理：三角形的两边之和大于第三边。
对于一些特殊的三角形，是否还存在其他特殊的关系？
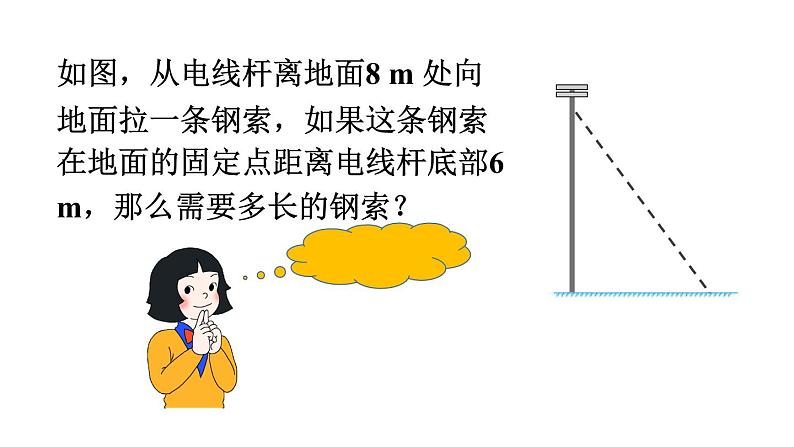
如图，从电线杆离地面8 m 处向地面拉一条钢索，如果这条钢索在地面的固定点距离电线杆底部6 m，那么需要多长的钢索？
1.在纸上画若干个直角三角形，分别测量它们的三条边，看看三边长的平方之间有怎么样的关系？
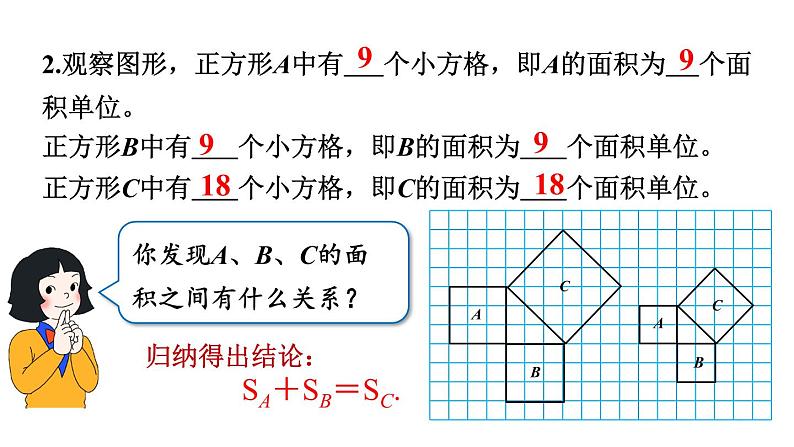
2.观察图形，正方形A中有 个小方格，即A的面积为 个面积单位。正方形B中有 个小方格，即B的面积为 个面积单位。正方形C中有 个小方格，即C的面积为 个面积单位。
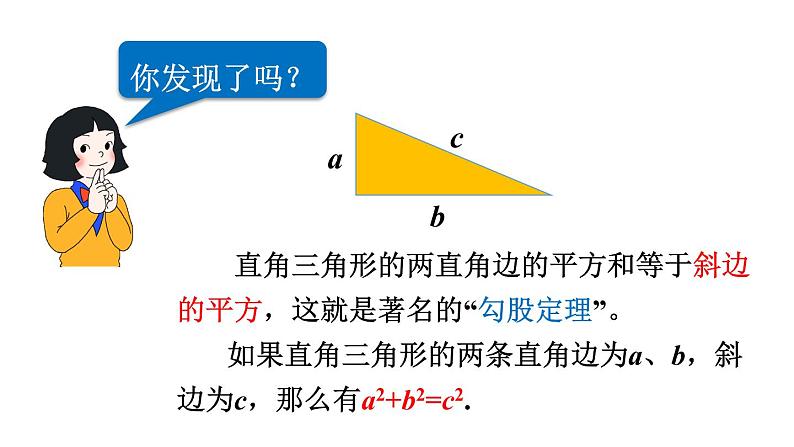
你发现A、B、C的面积之间有什么关系？
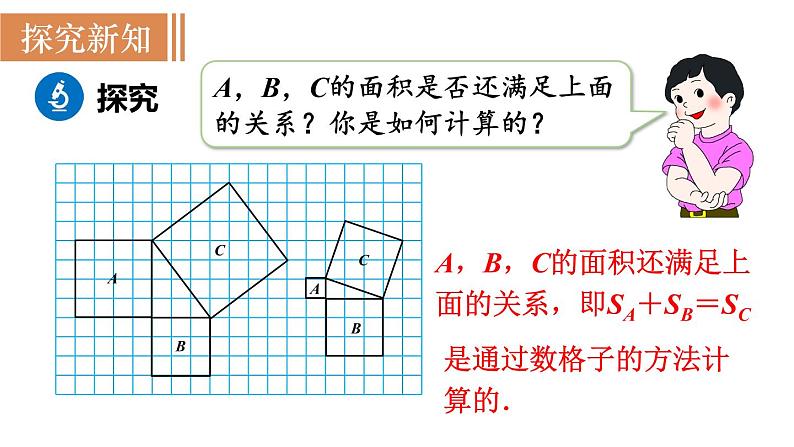
A，B，C的面积是否还满足上面的关系？你是如何计算的？
A，B，C的面积还满足上面的关系，即SA＋SB＝SC
是通过数格子的方法计算的．
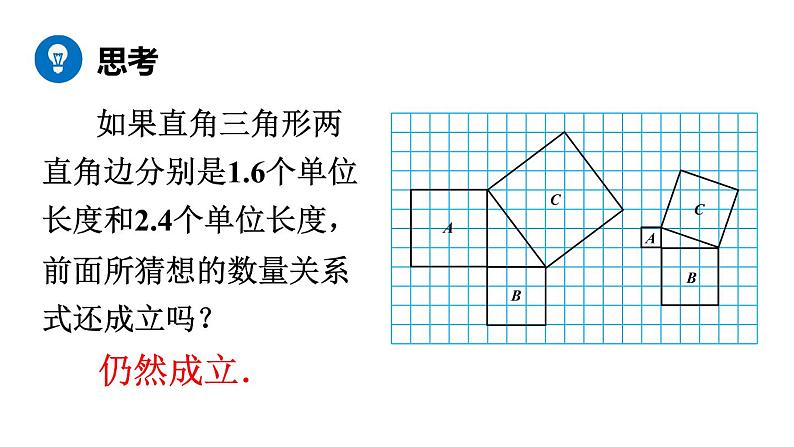
如果直角三角形两直角边分别是1.6个单位长度和2.4个单位长度，前面所猜想的数量关系式还成立吗？
直角三角形的两直角边的平方和等于斜边的平方，这就是著名的“勾股定理”。 如果直角三角形的两条直角边为a、b，斜边为c，那么有a2+b2=c2.
我国古代称直角三角形的较短的直角边为勾，较长的直角边为股，斜边为弦，这便是勾股定理的由来。
例1 在△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边．(1)若a＝6，b＝8，求c的值；(2)若a＝5，c＝13，求b的值．
解：(1)由勾股定理，得c2＝a2＋b2＝62＋82＝100.∵102＝100，∴c＝10；(2)由勾股定理，得b2＝c2－a2＝132－52＝144.∵122＝144，∴b＝12.
例2 如下表，表中每行所给的三个数a，b，c，有a运用勾股定理a2＋b2＝c2，及c＝b＋1求解．
∴当a＝19时，b＝180，c＝181.
解得b＝ ，c＝ ，
如果直角三角形两直角边长分别为a，b，斜边长为 c ，那么a2+b2=c2
1.求下图中字母所代表的正方形的面积。
解:A 所代表的正方形的面积是625；B 所代表的正方形的面积是144．
2.如图，点E在正方形ABCD内，且∠AEB＝90°，AE＝6，BE＝8，则阴影部分的面积是 ( ) A.48 B.60 C.76 D.80
3．如图，有两棵树，一棵高10m，另一棵高4m，两树相距8m．一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行 （ ）A.8m B.10m C.12m D.14m
4．如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为9cm，则正方形A，B，C，D的面积的和是____cm2.