北师大版八年级上册5 三角形的内角和定理教课课件ppt

这是一份北师大版八年级上册5 三角形的内角和定理教课课件ppt，共16页。PPT课件主要包含了导入新课，探究新知，应用举例，课堂小结，三角形的内角和定理，随堂练习等内容，欢迎下载使用。
我的面积比你大，所以我的内角和也比你大
那可不好说噢，你自己量量看
大三角形用量角器量了量自己的内角和，就不再说话了．你知道为什么吗？
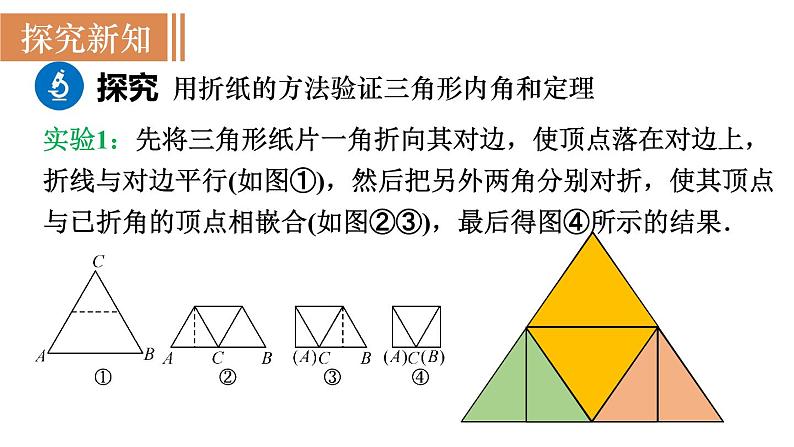
用折纸的方法验证三角形内角和定理
实验1：先将三角形纸片一角折向其对边，使顶点落在对边上，折线与对边平行(如图①)，然后把另外两角分别对折，使其顶点与已折角的顶点相嵌合(如图②③)，最后得图④所示的结果．
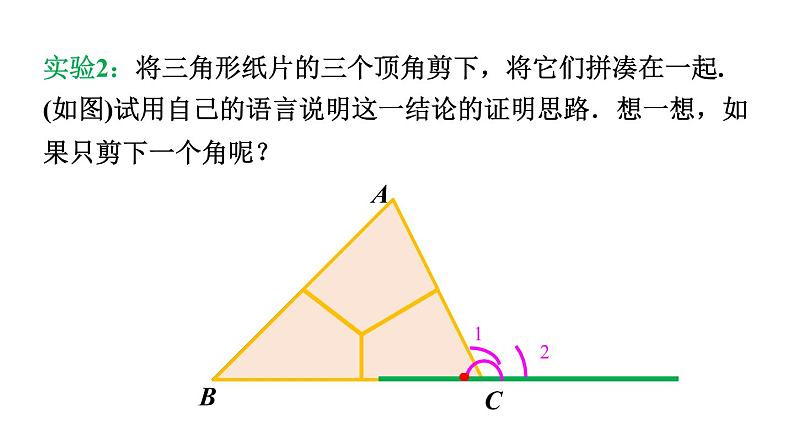
实验2：将三角形纸片的三个顶角剪下，将它们拼凑在一起. (如图)试用自己的语言说明这一结论的证明思路．想一想，如果只剪下一个角呢？
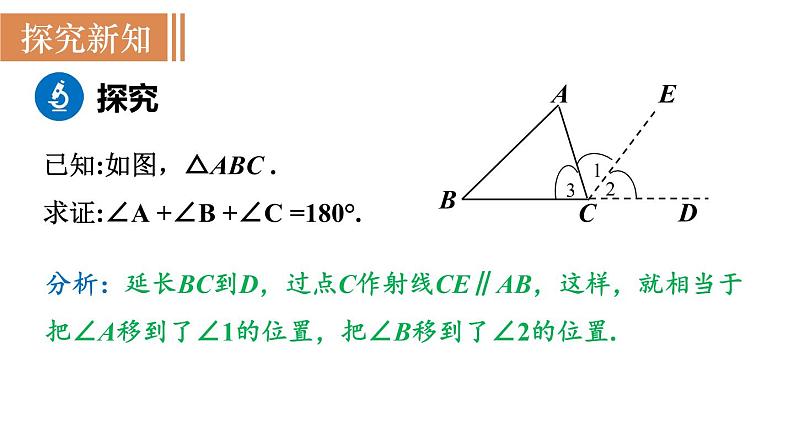
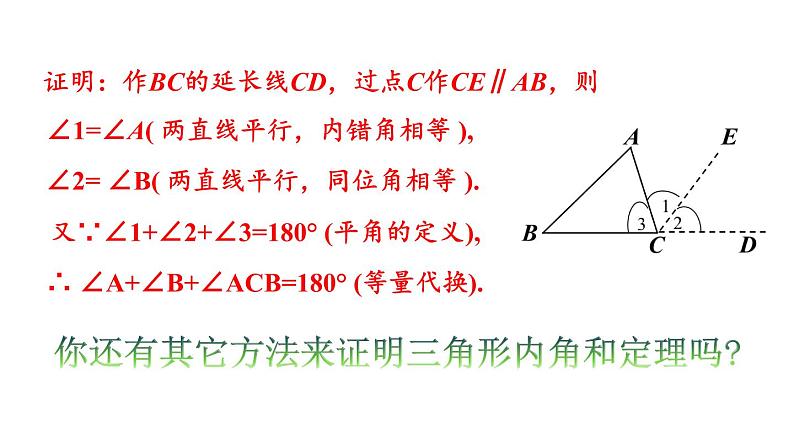
已知:如图，△ABC .求证:∠A +∠B +∠C =180°.
分析：延长BC到D，过点C作射线CE∥AB，这样，就相当于把∠A移到了∠1的位置，把∠B移到了∠2的位置.
证明：作BC的延长线CD，过点C作CE∥AB，则
∠1=∠A( 两直线平行，内错角相等 ),
∠2= ∠B( 两直线平行，同位角相等 ).
又∵∠1+∠2+∠3=180° (平角的定义),
∴ ∠A+∠B+∠ACB=180° (等量代换).
你还有其它方法来证明三角形内角和定理吗?
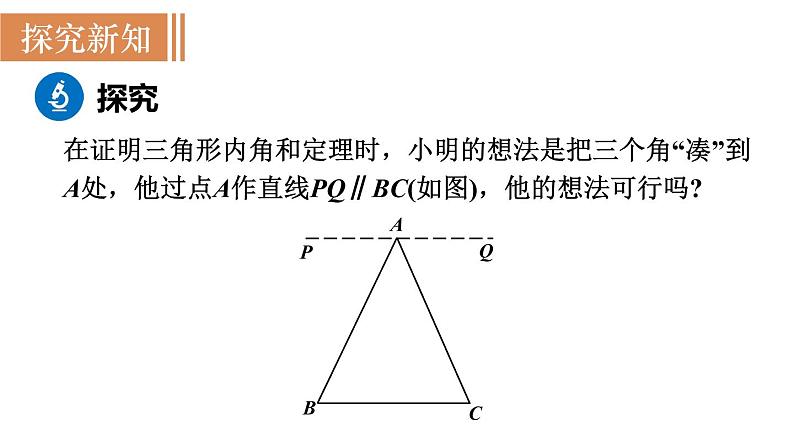
在证明三角形内角和定理时，小明的想法是把三个角“凑”到A处，他过点A作直线PQ∥BC(如图)，他的想法可行吗?
证明：过点A作PQ∥BC，则
∠1=∠B( 两直线平行,内错角相等 ),
∠2=∠C( 两直线平行,内错角相等 ),
又∵∠1+∠2+∠3=180° ( 平角的定义 ),
∴ ∠BAC+∠B+∠C=180° ( 等量代换 ).
例1 如图，在△ABC中，∠B=38°,∠C=62°, AD是△ABC的角平分线，求∠ADB的度数.
解：在△ABC中，∠B＋∠C＋∠BAC＝180°(三角形内角和定理)．∵∠B＝38°，∠C＝62°(已知)，
∴∠BAC＝180°－38°－62°＝80°(等式的性质)．∵AD平分∠BAC(已知)，∴∠BAD＝∠CAD＝ ∠BAC ＝ ×80°＝40°(角平分线的定义)．
在△ADB中，∠B＋∠BAD＋∠ADB＝180°(等式的性质)，∵∠B＝38°(已知)，∠BAD＝40°(已证)，∴∠ADB＝180°－38°－40°＝102°(等式的性质)．
例2 如图，AD，AE分别为△ABC的高线和角平分线，且∠B＝35°，∠C＝45°，求∠DAE的度数．
解：在△ABC中，∠B＝35°，∠C＝45°，∴∠BAC＝180°－(35°＋45°)＝100°.又∵AE平分∠BAC，∴∠CAE＝ ∠BAC＝ ×100°＝50°.在△ACD中，∠ADC＝90°，∠C＝45°，∴∠CAD＝180°－90°－45°＝45°.∴∠DAE＝∠CAE－∠CAD＝50°－45°＝5°.
了解添加辅助线的方法及其目的
三角形内角和等于180 °
1. 直角三角形的两锐角之和是多少度？证明你的结论.
证明：因为三角形内角和为180°，而直角为90°，所以直角三角形两锐角之和为180°-90°= 90°
2. 正三角形的一个内角是多少度？证明你的结论.
证明：因为等边三角形三个内角相等.所以正三角形每一个内角的度数为 ×180°＝60°
3. 已知：如图，在△ABC中，∠A=60°，∠C=70°，点D，E分别在AB和AC上，且DE//BC.求证：∠ADE=50°.
证明：∵DE∥BC（已知）∴∠AED＝∠C ＝70°（两直线平行，同位角相等）又∵∠A＝60°（已知）∴∠ADE＝180°－70°－60°＝50°（三角形内角和定理）