2020-2021学年第25章 图形的相似25.4 相似三角形的判定优秀当堂达标检测题

2022-2023年冀教版数学九年级上册25.4

《相似三角形的判定》课时练习

一              、选择题

1.如图，在△ABC与△ADE中，∠BAC=∠D，要使△ABC与△ADE相似，还需满足下列条件中的(　 　)

A.=        B.=         C.=        D.=

2.在Rt△ABC和Rt△DEF中，∠C=∠F=90°，下列条件中不能判定这两个三角形相似的是(　 　)

A.∠A=45°，∠D=45°

B.AC=9，BC=12，DF=6，EF=8

C.AC=3，BC=4，DF=6，DE=8

D.AB=10，AC=8，DE=15，EF=9

3.在三角形纸片ABC中，AB=8，BC=4，AC=6，按下列方法沿虚线剪下，能使阴影部分的三角形与△ABC相似的是(　 　)

4.如图，在△ABC中，DE∥BC，∠ADE=∠EFC，AD∶DB=5∶3，FC=6，则DE的长为(　 　)

A.6         B.8           C.10        D.12

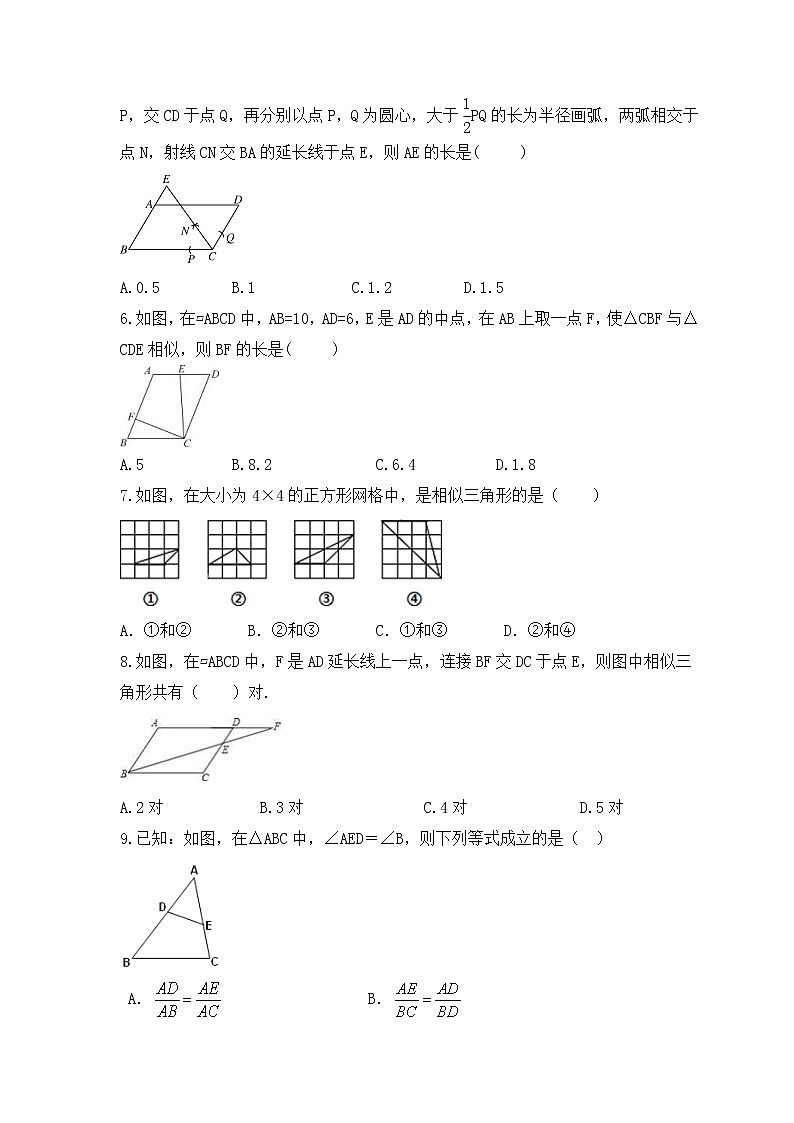
5.如图，在▱ABCD中，AB=2，BC=3.以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是(　 　)

A.0.5         B.1            C.1.2         D.1.5

6.如图，在▱ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF与△CDE相似，则BF的长是(　 　)

A.5           B.8.2             C.6.4          D.1.8

7.如图，在大小为4×4的正方形网格中，是相似三角形的是（　　）

A．①和②    B．②和③    C．①和③    D．②和④

8.如图，在▱ABCD中，F是AD延长线上一点，连接BF交DC于点E，则图中相似三角形共有（　　）对.

A.2对           B.3对             C.4对             D.5对

9.已知：如图，在△ABC中，∠AED＝∠B，则下列等式成立的是（  ）

 A．                  B．

C．                  D．

10.如图,P是Rt△ABC的斜边BC上异于B、C的一点，过P点作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有（     ）

  A.1条                         B.2条                      C.3条                            D.4条

二              、填空题

11.如图所示，已知点E在AC上，若点D在AB上，则满足条件　　(只填一个条件)，

使△ADE与原△ABC相似.

12.如图,在平行四边形ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于G,延长BE交CD的延长线于点H,则图中的相似三角形共有      对．

13.如图，若△ADE∽△ACB，且=，DE=10，则CB=       .

14.在△ABC中，AB=8，AC=6，在△DEF中，DE=4，DF=3，要使△ABC与△DEF相似，则需要添加一个条件是_____________________.(写出一种情况即可)

15.如图，在正方形网格上有6个三角形：①△ABC，②△CDB，③△DEB，④△FBG，⑤△HGF，⑥△EKF．在②～⑥中，与①相似的三角形的个数是                ．

16.如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP=　　.

三              、解答题

17.如图，点D，E分别为△ABC的边AC，AB上的点，BD，CE交于点O，且=，

试问△ADE与△ABC相似吗？请说明理由．

18.如图，已知∠DAB=∠EAC，∠ADE=∠ABC.求证：

(1)△ADE∽△ABC；

(2)=.

19.如图，在△ABC中，∠BAC=90°，M是BC的中点，过点A作AM的垂线，交CB的延长线于点D.求证：△DBA∽△DAC.

20.如图，在△ABC中，AB=AC=1，BC=，在AC边上截取AD=BC，连接BD.

(1)通过计算，判断AD2与AC·CD的大小关系；

(2)试说明△ABC∽△BDC.

参考答案

1.C

2.C

3.D

4.C

5.B.

6.B

7.D

8.B

9.B

10.C

11.答案为：∠B=∠AED.

12.答案为：4．

13.答案为：15

14.答案为：∠A=∠D(或BC∶EF=2∶1)

15.答案为：3个；

16.答案为：1或4或2.5.

17.解：相似．理由如下：

因为=，∠BOE=∠COD，∠DOE=∠COB，

所以△BOE∽△COD，△DOE∽△COB.

所以∠EBO=∠DCO，∠DEO=∠CBO.

因为∠ADE=∠DCO＋∠DEO，∠ABC=∠EBO＋∠CBO，

所以∠ADE=∠ABC.

又因为∠A=∠A，

所以△ADE∽△ABC.

18.证明：(1)∵∠DAB=∠EAC，

∴∠DAB＋∠BAE=∠EAC＋∠BAE.

∴∠DAE=∠BAC.

又∵∠ADE=∠ABC，∴△ADE∽△ABC.

(2)∵△ADE∽△ABC，∴=.

∵∠DAB=∠EAC，

∴△ADB∽△AEC.∴=.

19.证明：∵∠BAC=90°，点M是BC的中点，

∴AM=CM，

∴∠C=∠CAM，

∵DA⊥AM，

∴∠DAM=90°，

∴∠DAB=∠CAM，

∴∠DAB=∠C，

∵∠D=∠D，

∴△DBA∽△DAC.

20.解：(1)AD2=AC·CD　(2)略