北师大版七年级上册3.2 代数式优秀随堂练习题

3.2 代数式精选练习

基础篇

一、单选题

1．（2022·安徽·定远县第一初级中学七年级期末）已知代数式的值是3，则的值是（       ）

A．2 B．4 C．5 D．6

【答案】C

【分析】原式后两项变形，把已知代数式的值代入计算即可求出值．

【详解】解：∵x+2y=3，

∴原式=-1+2（x+2y）

=-1+6

=5．

故选：C．

【点睛】此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．

2．（2022·海南鑫源高级中学七年级期末）当x=1，代数式+2x+1的值是（　　）

A．-4 B．2 C．4 D．0

【答案】C

【分析】直接把x=1代入计算即可．

【详解】解：当x=1时，

+2x+1

=+2×1+1

=1+2+1

=4．

故选：C．

【点睛】本题考查代数式求值，有理数的混合运算，掌握有理数的运算法则和运算顺序是解决本题的关键．

3．（2021·浙江·杭州市余杭区良渚实验学校七年级阶段练习）若，则代数式的值是（     ）

A． B． C． D．

【答案】A

【分析】把化为，再根据，整体代入计算即可．

【详解】∵，

∴，

∴

，

故选：A．

【点睛】本题考查了代数式的求值，掌握整体代入法求代数式的值，把作为一个整体是解题关键．

4．（2022·山东威海·期末）如果代数式的值为5，那么代数式的值为（   ）

A． B．11 C．7 D．

【答案】A

【分析】先根据题意得到，然后整体代入到中进行求解即可．

【详解】解：∵代数式的值为5，

∴，

∴，

∴，

故选A．

【点睛】本题主要考查了代数式求值，正确得到是解题的关键．

5．（2021·河南洛阳·七年级期中）已知，则的值是（       ）

A．1 B．0 C． D．2

【答案】C

【分析】先根据非负数的性质求出、的值，再把、的值代入代数式进行计算即可．

【详解】解：根据题意得，，，

解得，，

所以，．

故选：C．

【点睛】本题主要考查了绝对值非负数，平方数非负数的性质，根据几个非负数的和等于0，则每一个算式都等于0列式是解题的关键．

6．（2022·河南郑州·七年级期末）乐乐在数学学习中遇到了神奇的“数值转换机”，按如图所示的程序运算，若输入一个有理数，则可相应的输出一个结果．若输入的值为，则输出的结果为（       ）

A． B． C． D．

【答案】B

【分析】把x=代入程序中计算，判断结果比0小，以此类推，得到结果大于0，输出即可．

【详解】解：把x=代入运算程序得：（-1）×（-3）-8=3-8=-5<0，

把x=-5代入运算程序得：（-5）×（-3）-8=15-8=7>0，

输出的结果y为7．

故选B．

【点睛】本题考查了代数式求值，弄清题中的程序流程是解本题的关键．

二、填空题

7．（2022·山东·泰安市泰山区树人外国语学校期末）如果，那么________．

【答案】-1

【分析】根据非负数的性质求出a、b的值，然后代值计算即可．

【详解】解：∵，，

∴，

∴，

∴，

∴，

故答案为：-1．

【点睛】本题主要考查了非负数的性质，代数式求值，有理数的乘方计算，正确根据非负数的性质求出a、b的值是解题的关键．

8．（2022·全国·七年级专题练习）已知a=-2.5，b=-4，则代数式的值是____________________；

【答案】-30

【分析】直接把a、b的值代入代数式求解即可．

【详解】解：∵a=-2.5，b=-4，

∴，

故答案为：-30．

【点睛】本题主要考查了代数式求值，含乘方的有理数混合计算，熟知含乘方的有理数混合计算法则是解题的关键．

9．（2021·湖南·安仁县思源实验学校七年级期中）若a、b互为相反数，c、d互为倒数，则2021a+3cd+2021b= ________；

【答案】3

【分析】根据互为相反数的特点，得：a+b=0；根据互为倒数的特点，得：cd=1，代入求解即可．

【详解】解：∵a，b互为相反数，

∴a+b=0；

∵c，d互为倒数，

∴cd=1．

∴2021a+3cd+2021b

=2021（a+b）+3cd

=0+3

=3．

故答案为：3．

【点睛】本题主要考查了有理数的混合运算，相反数、倒数的定义和性质及求代数式的值的方法．注意：互为相反数的两个数的和为0；互为倒数的两个数的积为1．

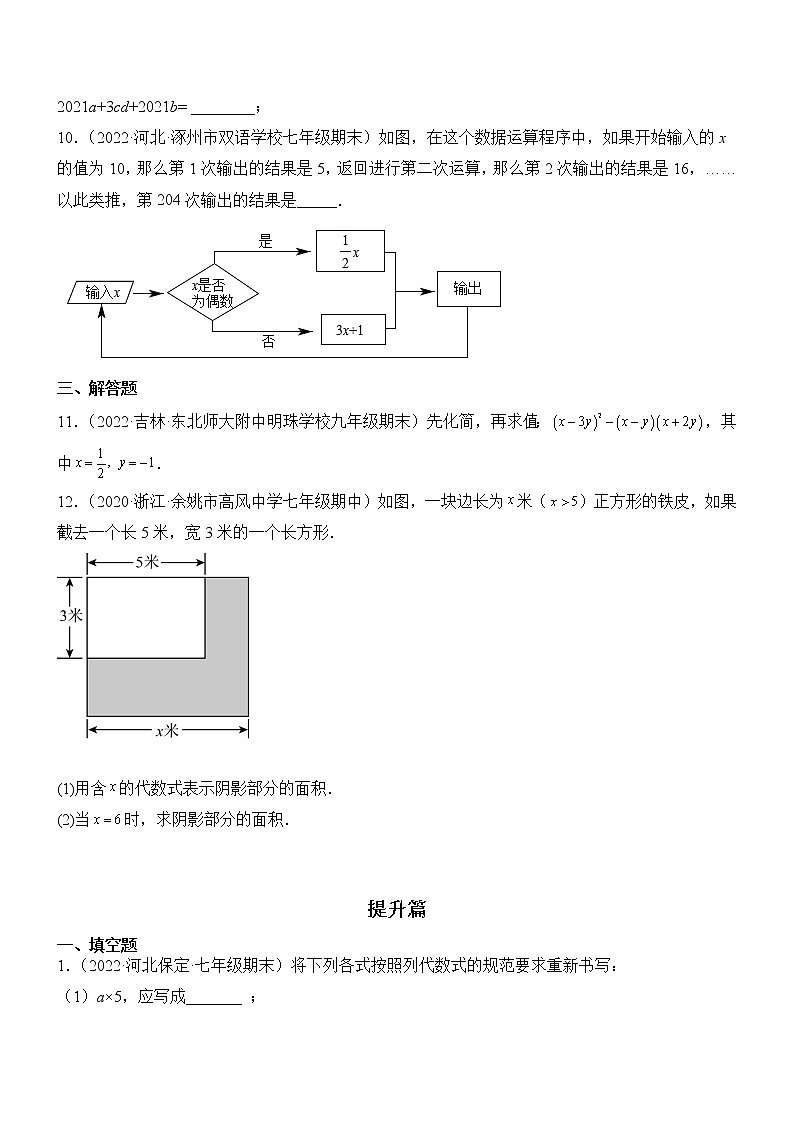
10．（2022·河北·涿州市双语学校七年级期末）如图，在这个数据运算程序中，如果开始输入的x的值为10，那么第1次输出的结果是5，返回进行第二次运算，那么第2次输出的结果是16，……以此类推，第204次输出的结果是_____．

【答案】1

【分析】根据数据运算程序，从第1次开始往后逐个计算输出结果，直到找出规律即可求解．

【详解】解：由数据运算程序得，如果开始输入的x的值为10，那么：

第1次输出的结果是5，

第2次输出的结果是16，

第3次输出的结果是8，

第4次输出的结果是4，

第5次输出的结果是2，

第6次输出的结果是1，

第7次输出的结果是4，

……

综上可得，从第4次开始，每三个一循环，

由 可得第204次输出的结果与第6次输出的结果相等．

故答案为：1．

【点睛】本题主要考查了代数式求值问题，解题的关键是通过计算特殊结果发现一般规律．

三、解答题

11．（2022·吉林·东北师大附中明珠学校九年级期末）先化简，再求值：，其中．

【答案】14.5

【分析】先根据完全平方公式和多项式乘以多项式法则计算，再根据整式的加减法法则计算，然后代入计算即可．

【详解】原式=

=

=．

当，时，

原式=

=

=14.5．

【点睛】本题主要考查了整式的化简求值，掌握整式的运算法则是化简的关键．

12．（2020·浙江·余姚市高风中学七年级期中）如图，一块边长为米（）正方形的铁皮，如果截去一个长5米，宽3米的一个长方形．

(1)用含的代数式表示阴影部分的面积．

(2)当时，求阴影部分的面积．

【答案】(1)平方米；

(2)21平方米．

【分析】（1）用正方形的面积减去矩形的面积即可；

（2）把x的值代入进行计算即可得解．

（1）

平方米；

（2）

当x＝6时，x2−15＝36−15＝21平方米．

【点睛】本题考查了列代数式，代数式求值，仔细观察图形表示出阴影部分的面积是解题的关键．

提升篇

一、填空题

1．（2022·河北保定·七年级期末）将下列各式按照列代数式的规范要求重新书写：

（1）a×5，应写成_______ ；       

（2）S÷t应写成_________；

（3），应写成______；

（4）, 应写成______.

【答案】     5a              

【分析】（1）根据代数式书写规范将数字因数写在代数式前省略乘号即可得到结果．

（2）根据代数式书写规范将除法算式写成分数形式即可得到结果．

（3）根据代数式书写规范将数字因数写在代数式前省略乘号，同时将相同字母的乘积写成乘方形式即可得到结果．

（4）根据代数式书写规范将数字因数的带分数化为假分数即可得到结果．

【详解】解：（1）a×5=5a，

故答案为∶5a；

（2）S÷t=，

故答案为∶；

（3），

故答案为∶；

（4）

故答案为∶．

【点睛】本题考查代数式书写规范，熟知代数式的书写规范要求是解题关键．

2．（2022·四川遂宁·八年级期末）若 ，则 =_____________．

【答案】1

【分析】根据得x+y=－3xy，分解整体代入计算即可．

【详解】因为，

所以x+y=－3xy，

所以

=1．

【点睛】本题考查了分式的条件求值，熟练掌握整体思想计算是解题的关键．

3．（2020·河南省洛阳市东升第二中学七年级期中）已知|x|＝3，|y|＝7，且xy<0，则x＋y的值等于________．

【答案】±4

【分析】根据绝对值的意义得到x＝±3，y＝±7，由xy<0，则x＝3，y＝﹣7或x＝﹣3，y＝7，然后把它们分别代入x＋y中计算即可．

【详解】解：∵|x|＝3，|y|＝7，

∴x＝±3，y＝±7，

而 xy<0，

∴x＝3，y＝﹣7或x＝﹣3，y＝7，

当x＝3，y＝﹣7时，x＋y＝3﹣7＝﹣4；

当x＝﹣3，y＝7时，x＋y＝﹣3＋7＝4．

故答案为±4．

【点睛】本题考查了绝对值：若a＞0，则|a|＝a；若a＝0，则|a|＝0；若a＜0，则|a|＝﹣a．

4．（2021·江苏·东海县驼峰中学七年级阶段练习）已知关于的方程只有一个解，那么的值为______．

【答案】10

【分析】首先根据方程只有一个解，可得a+2=0，x+1=0，即可求得a、x的值，再把a、x的值代入代数式求值即可．

【详解】解：方程只有一个解，

a+2=0，x+1=0，

解得a=-2，x=-1，

把a=-2，x=-1代入代数式，得

故答案为：10．

【点睛】本题考查了利用方程的解，求代数式的值，正确理解方程只有一个解，求得a、x的值是解决本题的关键．

5．（2022·浙江丽水·七年级期末）若实数，满足，，则________．

【答案】−1或5

【分析】根据绝对值的定义求出a、b的值，再代入计算即可．

【详解】解：∵|a|＝2，

∴a＝±2，

当a＝2时，|4−b|＝1−2＝−1，此时b不存在；

当a＝−2时，|4−b|＝3，

∴4−b＝3或4−b＝−3，

即b＝1或b＝7，

当a＝−2，b＝1时，a＋b＝−1；

当a＝−2，b＝7时，a＋b＝5．

故答案为：−1或5．

【点睛】本题考查绝对值的意义，理解绝对值的意义是正确解答的前提，求出a、b的值是正确解答的关键．

二、解答题

6．（2022·上海·七年级专题练习）已知，化简代数式并求值．

【答案】，96

【分析】根据非负性得出，，再按照去括号、合并同类项的顺序化简代数式，最后代入求值即可．

【详解】∵，

∴，，

解出得：，，

化简，得：

代入值，得．

【点睛】本题考查了非负性，整式的化简求值，熟练掌握整式的化简方法是解题的关键．

7．（2021·吉林·长春市第七十二中学七年级期中）某校餐厅计划购买12张餐桌和一批餐椅．现从甲、乙两商场了解到：同一型号的餐桌报价每张均为200元，餐椅报价每把均为50元．甲商场称：每购买一张餐桌赠送一把餐椅；乙商场场规定：所有餐桌、餐椅均按报价的八五折销售．设该校计划购买x把餐椅．

(1)当x＞12时，分别写出该校到甲、乙两商场购买所需餐桌、餐椅的总费用．

(2)当x＝40时，该校到哪家商场购买合算？请通过计算说明理由．

【答案】(1)，

(2)该校到乙商场购买合算

【分析】（1）根据购买费用=购买数量×购买单价分别表示出购买餐桌的费用和购买餐椅的费用进行求解即可；

（2）求出x=40时的值，比较可得．

（1）

解：设该校需购买x把椅子，在甲商场购买需要费用为元，在乙商场购买需要付费 元，由题意，得：

，

；

（2）

解：当x=40时，，

，

∵3800＞3740，

∴该校到乙商场购买合算．

【点睛】本题主要考查了列代数式和代数式求值，正确理解题意列出两个商场的费用的代数式是解题的关键．

8．（2022·山西晋城·七年级期末）如图，将长和宽分别是a、b的矩形纸片折成一个无盖的长方体纸盒，方案是在矩形纸片的四个角都剪去一个边长为x的正方形．

(1)用含a、b、x的代数式表示纸片剩余部分的面积；

(2)当，且剪去部分的正方形的边长为最小的正整数时，求无盖长方体纸盒的底面积；

(3)当，若x取整数，以x作为高，将纸片剩余部分折成无盖长方体，求长方体的体积最大值．

【答案】(1)

(2)48

(3)48

【分析】（1）根据图形可知剩余部分的面积＝长方形的面积﹣4个小正方形的面积，从而可以用代数式表示出来；

（2）根据题意可以求得正方形边长x的值，从而求出长方体纸盒的底面积．

（3）根据题意可以求得x的取值范围，然后由x取整数，从而可以分别求各种情况下长方体的体积，进而求出长方体体积的最大值．

（1）

由题意得，

纸片剩余部分的面积是ab﹣4x2；

（2）

设：正方形边长为x

由已知得，当a＝10，b＝8时，

S＝（a﹣2x）（b﹣2x）

＝（10﹣2x）×（8﹣2x）

∵边长为最小的正整数时

∴x＝1，

当x＝1时，S＝（10﹣2×1）（8﹣2×1）＝48，

即底面积是48．

（3）

由已知得，当a＝10，b＝8时，

V＝（a﹣2x）（b﹣2x）x

＝（10﹣2x）×（8﹣2x）×x

∵10﹣2x＞0且8﹣2x＞0，

解得，x＜4，

∵x取整数，

∴x＝1或x＝2或x＝3，

当x＝1时，V＝（10﹣2×1）（8﹣2×1）×1＝48，

当x＝2时，V＝（10﹣2×2）（8﹣2×2）×2＝48，

当x＝3时，V＝（10﹣2×3）（8﹣2×3）×3＝24，

即长方体的体积最大值是48．

【点睛】本题考查列代数式，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．