专练08（作图题）中考数学考点必刷题（解析版）

这是一份专练08（作图题）中考数学考点必刷题（解析版），共30页。试卷主要包含了如图，在平面直角坐标系中，A，如图，在平面直角坐标系中，，，等内容，欢迎下载使用。

专练08（作图题）（30道）
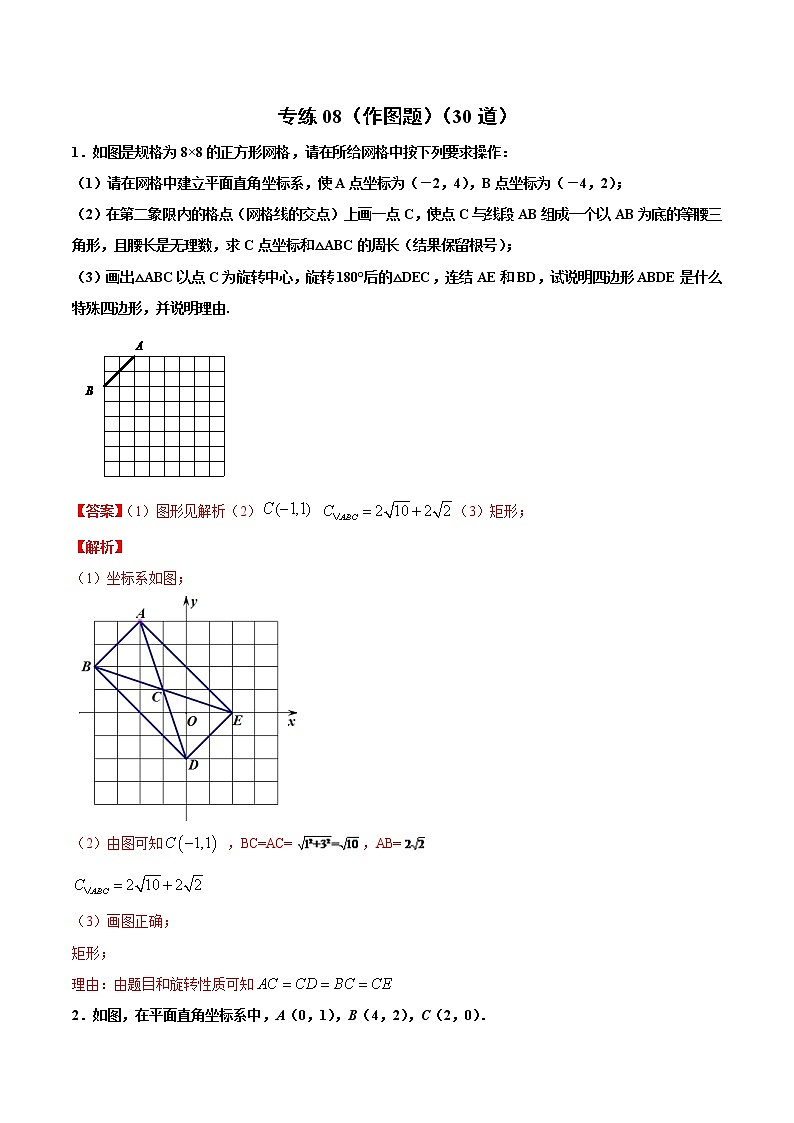
1．如图是规格为8×8的正方形网格，请在所给网格中按下列要求操作：
（1）请在网格中建立平面直角坐标系，使A点坐标为（－2，4），B点坐标为（－4，2）；
（2）在第二象限内的格点（网格线的交点）上画一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，求C点坐标和△ABC的周长（结果保留根号）；
（3）画出△ABC以点C为旋转中心，旋转180°后的△DEC，连结AE和BD，试说明四边形ABDE是什么特殊四边形，并说明理由.

【答案】（1）图形见解析（2） （3）矩形；
【解析】
（1）坐标系如图；

（2）由图可知 ，BC=AC=，AB=

（3）画图正确；
矩形；
理由：由题目和旋转性质可知
2．如图，在平面直角坐标系中，A（0，1），B（4，2），C（2，0）．
（1）将△ABC沿y轴翻折得到△A1B1C1，画出△A1B1C1；
（2）将△ABC绕着点（﹣1，﹣1）旋转180°得到△A2B2C2，画出△A2B2C2；
（3）线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到，直接写出旋转中心的坐标为　 　．

【答案】（1）详见解析；（2）详见解析；（3）（﹣2，﹣2）．
【解析】
解：（1）如图，△A1B1C1为所作；
（2）如图，△A2B2C2为所作；

（3）如图，线段B2C2可以看成是线段B1C1绕着点P逆时针旋转90°得到，此时P点的坐标为（﹣2，﹣2）．
故答案为（﹣2，﹣2）．
【点睛】
本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
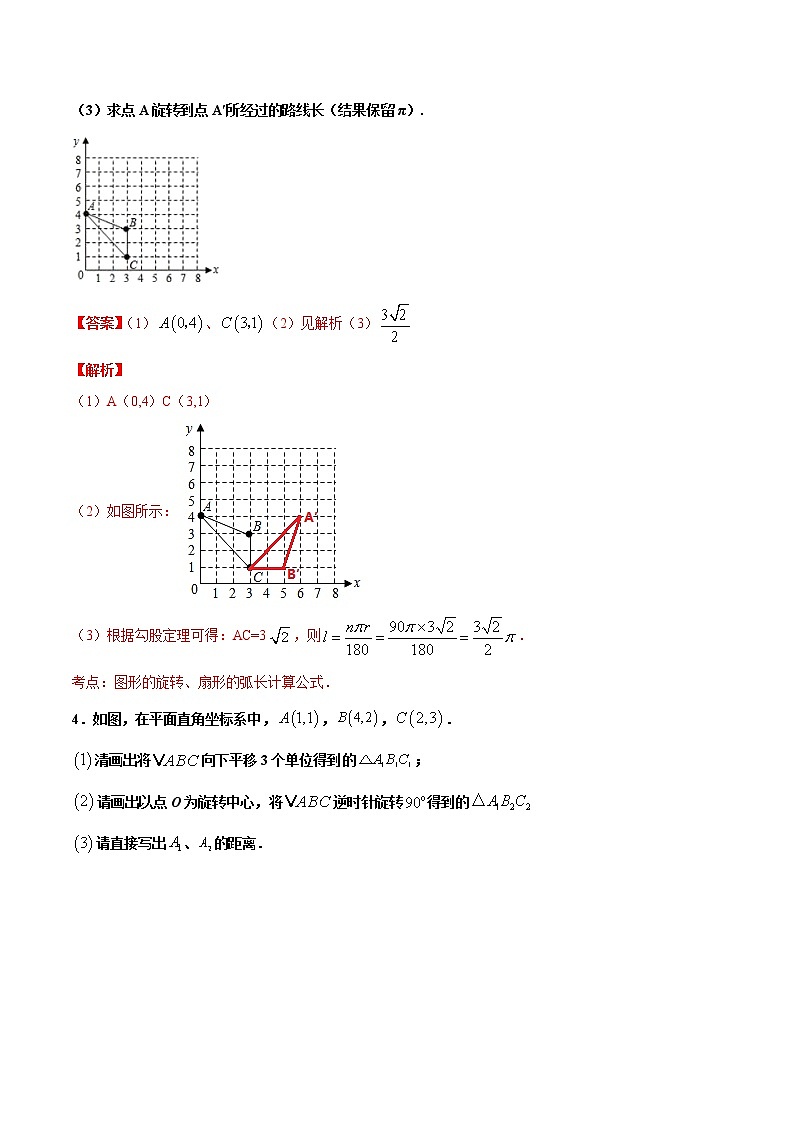
3．已知△ABC在平面直角坐标系中的位置如图所示.
（1）分别写出图中点A和点C的坐标；
（2）画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′；
（3）求点A旋转到点A′所经过的路线长（结果保留π）.

【答案】（1）、（2）见解析（3）
【解析】
（1）A（0,4）C（3,1）
（2）如图所示：
（3）根据勾股定理可得：AC=3，则．
考点：图形的旋转、扇形的弧长计算公式．
4．如图，在平面直角坐标系中，，，．
清画出将向下平移3个单位得到的；
请画出以点O为旋转中心，将逆时针旋转得到的
请直接写出、的距离．

【答案】（1）答案见解析；（2）答案见解析；（3）
【解析】
解：如图所示，即为所求；
如图所示，即为所求；
根据题意得：、的距离为．

【点睛】
考查了作图-旋转变换，平移变换，熟练掌握旋转与平移规律是解本题的关键．
5．如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（2，2），B（4,0），C（4，-4）.
（1）请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1；
（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y轴右侧画出△A2B2C2,；
（3）填空：△AA1A2的面积为________________.

【答案】3
【解析】
解：（1）如图所示：△A1B1C1，即为所求；
（2）如图所示：△A2B2C2，即为所求，

（3）△AA1A2的面积=×6=3.
点睛：本题考查了利用位似变换作图，利用轴对称变换作图，熟练掌握网格结构准确找出对应点的位置是解题关键.
6．如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别A（1，4），B（2，0），C（3，2）
（1）画出将△ABC沿AC翻折得到的△AB1C1；
（2）画出将△ABC沿x轴翻折得到的△A2BC2；
（3）观察发现：△A2BC2可由△AB1C绕点　 　（填写坐标）旋转得到
（4）在旋转过程中，点B1经过的路径长为　 　．

【答案】（1）见解析；（2）见解析；（3）（5，0）；（4）.
【解析】
解：（1）如图：
（2）如图：
（3）（5，0）
（4）B1经过的路径是以（5，0）为圆心，BB1为半径的圆弧，
∴C＝×2×π×3＝π；

【点睛】
本题考查三角形的旋转；掌握图象的旋转规律，准确判断点B1的轨迹是解题的关键．
7．如图，在平面直角坐标系中，的三个顶点分别为，，．
将向右平移6个单位后得到，请在图中画出，并写出点坐标；
图中点与点B关于直线l成轴对称，请在图中画出直线l及关于直线l对称的，并直接写出直线l对应的函数关系式．

【答案】画图见解析，；画图见解析，．
【解析】
如图所示：，即为所求，；

作直线l，，即为所求；
直线l对应的函数关系式为：．
【点睛】
此题主要考查了轴对称变换以及平移变换，正确得出对应点位置是解题关键．
8．如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．
（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；
（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）

【答案】（1）画图见解析；（2）画图见解析；（3）三角形的形状为等腰直角三角形．
【解析】
（1）如图所示，△A1B1C1即为所求；

（2）如图所示，△A2B2C2即为所求；
（3）三角形的形状为等腰直角三角形，OB=OA1=，A1B==，
即OB2+OA12=A1B2，
所以三角形的形状为等腰直角三角形．
【点睛】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
9．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
【答案】解：（1）如图所示：点A1的坐标（2，﹣4）。
（2）如图所示，点A2的坐标（﹣2，4）。

10．如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.

(1)画出△ABC关于y轴对称的△A1B1C1.
(2)画出△ABC绕点O按逆时针方向旋转90°后的△A2B2C2.
(3)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
【答案】见解析
【解析】
解：（1）如图，△A1B1C1即为所求．

（2）如图，△A2B2C2即为所求．
（3）△A1B1C1和△A2B2C2成轴对称，对称轴为直线A1B．
11．（如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.
(1) 请画出△ABC向左平移5个单位长度后得到的△ABC；
(2) 请画出△ABC关于原点对称的△ABC；
(3) 在轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.

【答案】（1）图形见解析；
（2）图形见解析；
（3）图形见解析，点P的坐标为：（2，0）
【解析】

（1）△A1B1C1如图所示；
（2）△A2B2C2如图所示；
（3）△PAB如图所示，点P的坐标为：（2，0）
【点睛】
1、图形的平移；2、中心对称；3、轴对称的应用
12．如图，在平面直角坐标系xOy中，每个小正方形的边长都为1，和的顶点都在格点上，回答下列问题：
可以看作是经过若干次图形的变化平移、轴对称、旋转得到的，写出一种由得到的过程：______；
画出绕点B逆时针旋转的图形；
在中，点C所形成的路径的长度为______．

【答案】（1）先沿y轴翻折，再向右平移1个单位，向下平移3个单位；先向左平移1个单位，向下平移3个单位，再沿y轴翻折；（2）见解析；（3）．
【解析】
解：（1）答案不唯一例如：先沿y轴翻折，再向右平移1个单位，向下平移3个单位；先向左平移1个单位，向下平移3个单位，再沿y轴翻折．

（2）分别将点C、A绕点B逆时针旋转得到点 、 ，如图所示，△即为所求；
（3）点C所形成的路径的长为：．
故答案为（1）先沿y轴翻折，再向右平移1个单位，向下平移3个单位；先向左平移1个单位，向下平移3个单位，再沿y轴翻折；（2）见解析；（3）π．
．
【点睛】
本题考查坐标与图形变化旋转，平移，对称，解题时需要注意：平移的距离等于对应点连线的长度，对称轴为对应点连线的垂直平分线，旋转角为对应点与旋转中心连线的夹角的大小．
13．如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣4，0），C（0，0）
（1）画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；
（2）画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O；
（3）在x轴上存在一点P，满足点P到A1与点A2距离之和最小，请直接写出P点的坐标．

【答案】（1）作图见解析；（2）作图见解析；（3）P（，0）．
【解析】
解：（1）如图所示，△A1B1C1为所求做的三角形；
（2）如图所示，△A2B2O为所求做的三角形；
（3）∵A2坐标为（3，1），A3坐标为（4，﹣4），
∴A2A3所在直线的解析式为：y=﹣5x+16，
令y=0，则x=，
∴P点的坐标（，0）．

考点：平移变换；旋转变换；轴对称-最短路线问题．
14．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．

①把△ABC向上平移5个单位后得到对应的△A1B1C1，画出△A1B1C1，并写出C1的坐标；
②以原点O为对称中心，画出△ABC与关于原点对称的△A2B2C2，并写出点C2的坐标；
③以原点O为旋转中心，画出把△ABC顺时针旋转90°的图形△A3B3C3，并写出C3的坐标．
【答案】（1）作图见解析，（4，4）；（2）作图见解析，（-4，1）；（3）作图见解析；（-1，-4）．
【解析】
（1）如图所示：C1的坐标为：（4，4）；

（2）如图所示：C2的坐标为：（-4，1）；
（3）如图所示：C3的坐标为：（-1，-4）．
考点: 1.作图-旋转变换；2.作图-平移变换．
15．如图，在平面直角坐标系xOy中，点，，．
以点C为旋转中心，把逆时针旋转，画出旋转后的△ ；
在的条件下，
点A经过的路径 的长度为______结果保留；
点的坐标为______．

【答案】（1）见解析；（2）①；②.
【解析】
解：（1）如图所示，即为所求；

（2）①，，
点A经过的路径的长为，
故答案为：；
②由图知点的坐标为，
故答案为：．
故答案为：（1）见解析；（2）①；②.
【点睛】
本题考查作图旋转变换，解题的关键是根据旋转角度、旋转方向、旋转中心作出对应点．
16．在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．
（1）将△ABC沿x轴方向向左平移6个单位长度，画出平移后得到的△A1B1C1；
（2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2；
（3）直接写出点B2，C2的坐标．

【答案】（1）答案见解析；（2）答案见解析；（3）点B2（4，－2），C2（1，－3）．
【解析】
解：（1）如图，△A1B1C1即为所求；
（2）如图，△AB2C2即为所求，点B2（4，﹣2），C2（1，﹣3）．

17．如图，在每个小正方形的边长均为1的方格纸中，线段AB的端点A、B均在小正方形的顶点上．
（1）在方格纸中画出以AB为一条直角边的等腰直角△ABC，顶点C在小正方形的顶点上；
（2）在方格纸中画出△ABC的中线BD，将线段DC绕点C顺时针旋转90°得到线段CD′，画出旋转后的线段CD′，连接BD′，直接写出四边形BDCD′的面积．

【答案】（1）画图见解析；（2）画图见解析；四边形BDCD′的面积为10．
【解析】
（1）如图所示：△ABC即为所求；
（2）如图所示：CD′即为所求，
BD=DC=，
四边形BDCD′的面积为：×=10．

【点睛】
本题考查了旋转变换以及等腰直角三角形的性质，正确得出对应点位置是解题的关键．
18．如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．
（1）画出△ABC关于x对称的△A1B1C1；
（2）以原点O为位似中心，在x轴的上方画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2，并求出△A2B2C2的面积．

【答案】（1）作图见解析；（2）作图见解析，28．
【解析】
解：（1）如图所示，△A1B1C1就是所求三角形；
（2）如图所示，△A2B2C2就是所求三角形．
如图，分别过点A2、C2作y轴的平行线，过点B2作x轴的平行线，交点分别为E、F，∵A（﹣1，2），B（2，1），C（4，5），△A2B2C2与△ABC位似，且位似比为2，∴A2（﹣2，4），B2（4，2），C2（8，10），∴=8×10﹣×6×2﹣×4×8﹣×6×10=28．

点睛：本题考查作图﹣位似变换，作图轴对称变换等知识，解题的关键是理解位似变换、轴对称变换的定义，属于中考常考题型．
19．如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）．
（1）按下列要求作图：
①将△ABC向左平移4个单位，得到△A1B1C1；
②将△A1B1C1绕点B1逆时针旋转90°，得到△A2B2C2．
（2）求点C1在旋转过程中所经过的路径长．

【答案】（1）①见解析；②见解析；（2）2π．
【解析】
（1）①如图，△A1B1C1为所作；
②如图，△A2B2C2为所作；

（2）点C1在旋转过程中所经过的路径长＝
【点睛】
本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移的性质．
20．如图所示，在平面直角坐标系中，△ABC各顶点的坐标分别为A（4，0），B（－1，4），C（－3，1）.
(1)作出△A′B′C′，使△A′B′C′和△ABC关于x轴对称；
(2)写出点A′， B′，C′的坐标；
(3)求△ABC的面积.

【答案】（1）见解析；（2）（4，0），（﹣1，﹣4），（﹣3，﹣1）；（3）11.5．
【解析】
（1）如图所示：△A′B′C′，即为所求；

（2）点A′的坐标为（4，0），点B′的坐标为（﹣1，﹣4），点C′的坐标为（﹣3，﹣1）；
（3）△ABC的面积为：7×4﹣×2×3﹣×4×5﹣×1×7=11.5．
21．如图，在平面直角坐标系中有△ABC，其中A（﹣3，4），B（﹣4，2），C（﹣2，1）．把△ABC绕原点顺时针旋转90°，得到△A1B1C1．再把△A1B1C1向左平移2个单位，向下平移5个单位得到△A2B2C2．
（1）画出△A1B1C1和△A2B2C2．
（2）直接写出点B1、B2坐标．
（3）P（a，b）是△ABC的AC边上任意一点，△ABC经旋转平移后P对应的点分别为P1、P2，请直接写出点P1、P2的坐标．

【答案】（1）见解析；（2）B1（2，4）、B2（0，﹣1）；（3）P1（b，﹣a），P2（b﹣2，﹣a﹣5）．
【解析】
解：（1）如图所示，△A1B1C1和△A2B2C2即为所求：

（2）点B1坐标为（2，4）、B2坐标为（0，﹣1）；
（3）由题意知点P1坐标为（b，﹣a），点P2的坐标为（b﹣2，﹣a﹣5）．
【点睛】
考查了利用平移变换以及旋转变换进行作图，解题时注意：确定平移后图形的基本要素有两个：平移方向、平移距离．决定旋转后图形位置的因素为：旋转角度、旋转方向、旋转中心．
22．如图，在由边长为1的小正方形组成的网格图中，已知点O及△ABC的顶点均为网格线的交点．
（1）将△ABC绕着点B顺时针旋转90°，得到△A1BC1，请在网格中画出△A1BC1；
（2）以点O为位似中心，将△ABC放大为原来的三倍，得到△A'B'C'，请在网格中画出△A'B'C'．

【答案】（1）见解析；（2）见解析.
【解析】
解：（1）如图所示：△A1BC1，即为所求；
（2）如图所示：△A'B'C'，即为所求．

【点睛】
此题主要考查了位似变换以及旋转变换，正确得出对应点位置是解题关键．
23．如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．
（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．

【答案】（1）（2）作图见解析；（3）．
【解析】
解：（1）如答图，连接AA1，然后从C点作AA1的平行线且A1C1=AC，同理找到点B1，分别连接三点，△A1B1C1即为所求．
（2）如答图，分别将A1B1，A1C1绕点A1按逆时针方向旋转90°，得到B2，C2，连接B2C2，△A1B2C2即为所求．

（3）∵，
∴点B所走的路径总长=．
考点：1．网格问题；2．作图（平移和旋转变换）；3．勾股定理；4．弧长的计算．
24．如图(1)，方格图中每个小正方形的边长为1，点A、B、C都是格点．
(1)画出△ABC关于直线MN对称的△A1B1C1；
(2)写出AA1的长度；
(3)如图(2)，A、C是直线MN同侧固定的点，B是直线MN上的一个动点，在直线MN上画出点B，使AB+BC最小．

【答案】（1）如图所示见解析；（2）AA1的长度为：10；（3）如图所示见解析；点D即为所求，此时AD+DC最小．
【解析】
（1）如图所示：

△A1B1C1，即为所求；
（2）AA1的长度为：10；
（3）

如图所示：连接AC1，AC1与MB的交点D即为所求，此时AD+DC最小．
【点睛】
本题主要考查图形的轴对称和平面直角坐标系的有关概念,掌握图形的轴对称和平面直角坐标系的有关概念是解决本题的关键.
25．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点都在格点上．
（1）在所给的网格中画出与△ABC相似（相似比不为1）的△A1B1C1（画出一个即可）；
（2）在所给的网格中，将△ABC绕点C顺时针旋转90°得到△A2B2C，画出△A2B2C，并直接写出在此旋转过程中点A经过的路径长．

【答案】（1）画图见解析；（2）画图见解析，.
【解析】
（1）如图所示：△A1B1C1，即为所求；
（2）如图所示：△A2B2C，即为所求，点A经过的路径长为：=π．

【点睛】
本题主要考查了相似变换以及旋转变换，正确得出对应点位置是解题的关键．
26．如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．
（1）画出△ABC关于y轴的对称图形△A1B1C1，并写出B1点的坐标；
（2）画出△ABC绕原点O旋转180°后得到的图形△A2B2C2，并写出B2点的坐标；
（3）在x轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．

【答案】（1）画图见解析；（2）画图见解析；（3）画图见解析.
【解析】
(1)、△A1B1C1如图所示；B1点的坐标（-4,2）
(2)、△A2B2C2如图所示；B2点的坐标:（-4，-2）
(3)、△PAB如图所示，P（2，0）．

考点：(1)、作图-旋转变换；(2)、轴对称-最短路线问题；(3)、作图-平移变换．
27．如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．

（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△C；平移△ABC，若A的对应点的坐标为（0，-4），画出平移后对应的△；
（2）若将△C绕某一点旋转可以得到△，请直接写出旋转中心的坐标；
（3）在轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．
【答案】（1）如下图；（2）（，）；（3）（－2，0）．

【解析】
（1）画出△A1B1C与△A2B2C2如图

（2）如图所示,旋转中心的坐标为:（，-1）
(3) 如图所示,点P的坐标为（-2，0）.

28．已知△OAB在平面直角坐标系中的位置如图所示．请解答以下问题：
（1）按要求作图：先将△ABO绕原点O逆时针旋转90°得△OA1B1，再以原点O为位似中心，将△OA1B1在原点异侧按位似比2：1进行放大得到△OA2B2；
（2）直接写出点A1的坐标，点A2的坐标．

【答案】(1)见解析；（2）点A1的坐标为：（﹣1，3），点A2的坐标为：（2，﹣6）．
【解析】
（1）如图所示：△OA1B1，△OA2B2，即为所求；

（2）点A1的坐标为：（﹣1，3），点A2的坐标为：（2，﹣6）．
【点睛】
此题主要考查了位似变换以及旋转变换，正确得出对应点位置是解题关键．
29．△ABC在平面直角坐标系中的位置如图所示．

（1）画出△ABC关于y轴对称的△A1B1C1；
（2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；
（3）观察△A1B1C1和△A2B2C2，它们是否关于某条直线对称？若是，请在图上画出这条对称轴．
【答案】（1）见解析；（2）见解析，A2（6，4），B2（4，2），C2（5，1）；（3）△A1B1C1和△A2B2C2是轴对称图形，对称轴为图中直线l：x＝3,见解析.
【解析】
（1）由图知，A（0，4），B（﹣2，2），C（﹣1，1），∴点A、B、C关于y轴对称的对称点为A1（0，4）、B1（2，2）、C1（1，1），连接A1B1，A1C1，B1C1，得△A1B1C1；
（2）∵△ABC向右平移6个单位，∴A、B、C三点的横坐标加6，纵坐标不变，作出△A2B2C2，A2（6，4），B2（4，2），C2（5，1）；
（3）△A1B1C1和△A2B2C2是轴对称图形，对称轴为图中直线l：x=3．

【点睛】
本题考查了轴对称图形的性质和作图﹣平移变换，作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
30．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）的顶点、的坐标分别为，．

（1）请在如图所示的网格平面内作出平面直角坐标系；
（2）请作出关于轴对称的；
（3）点的坐标为　 　．
（4）的面积为　 　．
【答案】（1）见解析；（2）见解析；（3）；（4）4.
【解析】
解：（1）如图所示：
（2）如图所示：
（3）结合图形可得：；
（4） .

【点睛】
此题主要考查了作图−−轴对称变换，关键是确定组成图形的关键点的对称点位置．