初中数学5 一次函数的应用授课ppt课件

这是一份初中数学5 一次函数的应用授课ppt课件，共34页。PPT课件主要包含了创设情境温故探新，2y-x，合作交流探究新知，大于4t，小于4t，s海里，反馈练习巩固新知，ycm，课堂小结布置作业等内容，欢迎下载使用。

1. 什么是一次函数?
2. 一次函数的图象是什么？
３. 一次函数具有什么性质？
若两个变量x,y间的关系式可以表示成y=kx+b (k,b为常数,k≠0)的形式,则称y是x的一次函数.
常数项 b决定一次函数图象与 轴交点的位置.
(3) y=3+0.5x
(4) y=100－0.18x
k =0.5, b=3
k=-0.18, b=100
注意：一次函数书写一般写成(1) y=0.5x+ 3 (2) y= - 0.18x+100
指出下列格式中的k和b:
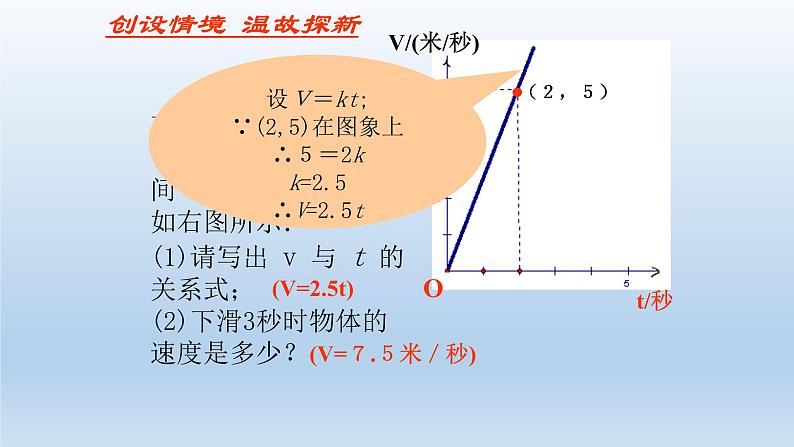
某物体沿一个斜坡下滑，它的速度 v （米/秒）与其下滑时间 t （秒）的关系如右图所示： (1)请写出 v 与 t 的关系式； (2)下滑3秒时物体的速度是多少？
设Ｖ＝kt;∵(2,5)在图象上∴５＝2kk=2.5∴V=2.5t
确定正比例函数的表达式需要几个条件？确定一次函数的表达式呢？
例 在弹性限度内，弹簧的长度 y（厘米）是所挂物体质量 x（千克）的一次函数。一根弹簧不挂物体时长14.5厘米；当所挂物体的质量为3千克时，弹簧长16厘米。请写出 y 与x之间的关系式，并求当所挂物体的质量为4千克时弹簧的长度。
解：设y=kx+b(k≠0) 由题意得： 16=3k+b,解得：b=14.5 ; k=0.5.所以在弹性限度内，当x=4时，y＝０.５×４＋14.5=16.5（厘米）.即物体的质量为４千克时，弹簧长度为１６.５厘米.
由于持续高温和连日无雨，某水库的蓄水量随着时间的增加而减少．干旱持续时间t(天)与蓄水量V(万米3)的关系如下图所示，回答下列问题：
(2)干旱持续10天，蓄水 量为多少？连续干旱 23天呢？
（1）水库干旱前的蓄水 量是多少？
(3)蓄水量小于400万米3时，将 发生严重干旱警报.干旱多少 天后将发出严重干旱警报？
(4)按照这个规律，预计持续干旱多少天水库将干涸？
由于高温和连日无雨，某水库蓄水量V（万米3)和干旱时间t（天）的关系如图：
合作探究：还能用其它方法解答本题吗？
（1）设v=kt+1200
（2）将t=60，V=0代入V=kt+1200中求的k= -20，V= -20 t+1200
（3）再代入各组 t 或 V 的值对应的求V 与 t 的值
例2 根据图象回答问题： （1）一箱汽油可供摩托车行驶多少千米？
解：观察图象，得(1)当y＝0时，x＝500,因此一箱汽油可供摩托车行驶500千米.
（3）摩托车的剩余油量小于1升时，摩托车将自动报警.行驶多少千米后，摩托车将自动报警？
（2）摩托车每行驶100千米消耗多少升汽油？
（2）x从0增加到100时，y从10减少到8，减少了2， 因此摩托车每行驶100千米2消耗升汽油.
（3）当y＝1时，x＝450，因此行驶了450千米后，摩托车将自动报警.
如图，l1反映了某公司产品的销售收入与销售量之间的关系，l2反映了该公司产品的销售成本与销售量之间的关系，根据图意填空：(1)当销售量为2吨时，销售收入= 元，销售成本= __元；
如图，l1反映了某公司产品的销售收入与销售量之间的关系，l2反映了该公司产品的销售成本与销售量之间的关系，根据图意填空：(2)当销售量为6吨时，销售收入= 元，销售成本= __元；
如图，l1反映了某公司产品的销售收入与销售量之间的关系，l2反映了该公司产品的销售成本与销售量之间的关系，根据图意填空：(3)当销售量等于 时，销售收入等于销售成本；
如图，l1反映了某公司产品的销售收入与销售量之间的关系，l2反映了该公司产品的销售成本与销售量之间的关系，根据图意填空：(4)当销售量 时，该公司赢利(收入大于成本)；当销售量 时，该公司亏损(收入小于成本)；
由此你能得到什么结论？
利用图象比较函数值的方法：
(1)先找交点坐标，交点处y1=y2；
(2)再看交点左右两侧，图象位于上方的直线函数值较大。
如图，l1反映了某公司产品的销售收入与销售量之间的关系，l2反映了该公司产品的销售成本与销售量之间的关系，根据图意填空：(5) l1对应的函数表达式是 ， l2对应的函数表达式是 。
例3、我边防局接到情报，近海处有一可疑船只A正向公海方向行驶，边防局迅速派出快艇B追赶，图中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。
下图中 l1 ，l2 分别表示 B 离岸起两船相对于海岸的距离ｓ与追赶时间ｔ之间的关系。
根据图象回答下列问题：
（1）哪条线表示 B 到海岸距离与追赶时间之间的关系？
解：观察图象，得　　当t＝0时，B距海岸0海里，即　　　S＝0，故 l1 表示 B 到海岸的距离与追赶时间之间的关系；
（2）A、B 哪个速度快？
t从0增加到10时， l2的纵坐标增加了2，l1的纵坐标增加了5，
即10分内，A 行驶了2海里，B 行驶了5海里，所以 B 的速度快。
可以看出，当t＝15时，l1上对应点在l2上对应点的下方。
这表明，15分钟时 B尚未追上 A。
（3）15分钟内 B 能否追上 A？
（4）如果一直追下去，那么 B 能否追上 A？
　　如图延伸l1 、l2 相交于点P。
因此，如果一直追下去，那么 B 一定能追上 A。
（5）当 A 逃到离海岸12海里的公海时，B 将无法对其进行检查。照此速度， B 能否在 A 逃入公海前将其拦截？
从图中可以看出，l1 与 l2 交点P的纵坐标小于12，
这说明在A逃入公海前，我边防快艇 B能够追上 A。
1、如图所示，已知直线AB和x轴交于点B,和y轴交于点A。 ①写出AB两点的坐标. ②求直线AB的表达式.　
③若一次函数图像y=ax+3的图象经过A(1, -2), 则a= . ④直线y=2x+b过点(1, -2), 则它与y轴交点坐标为( ).
①若y=kx的图象经过(1，2)点，那么它一定过（ ）A.（2，-1） B.（-0.5，-1） C.（-2，1） D.（-1，0.5）②根据条件确定一次函数表达式：y是x的正比例函数，当x=2时, y=6，求y与x的函数表达式
１. 若一次函数y=2x+b的图象经过Ａ(-1,1)则b=____,该函数图象经过点Ｂ(1，__）和点Ｃ（____，０）。
２. 如图，直线l是一次函数y=kx+b的图象，填空　(1)b=______,k=______; (2)当x=30时，y=______; (3)当y=30时，x=______。
解：设直线l为y=kx+b,　　　∵l与直线y=-2x平行，∴k= -2 又直线过点（０，２）， ∴２＝－２×0+b, ∴b=2 ∴原直线为y=-2x+2
３. 已知直线l与直线y=-2x平行，且与y轴交于点(0,2)，求直线l的解析式。
4.某植物t天后的高度为y厘米,图中反映了y与t之间的关系，根据图象回答下列问题：
(1)植物刚栽的时候多高？
（2）3天后该植物高度为多少？
（3）几天后该植物高度可达21cm?
（4）先写出y与t的关系式，再计算长到100cm需几天？
怎样求一次函数的表达式？
１.设——一次函数表达式 y=kx+b或者y=kx；２.代——将点的坐标代入y=kx+b中,列出关于K b 的方程３.解——解方程求出K b 值；４.定——把求出的k、b值代回到表达式中即可.
这种求函数解析式的方法叫做待定系数法
1、两直线交点的意义：
(1)几何意义：两直线交点是它们的公共点；
(2)代数意义：两直线交点的坐标同时满足两个解析式。
2、利用图象比较函数值的方法：
习题6.8：1，2题