高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案

这是一份高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案，共9页。学案主要包含了知识重温，小题热身等内容，欢迎下载使用。
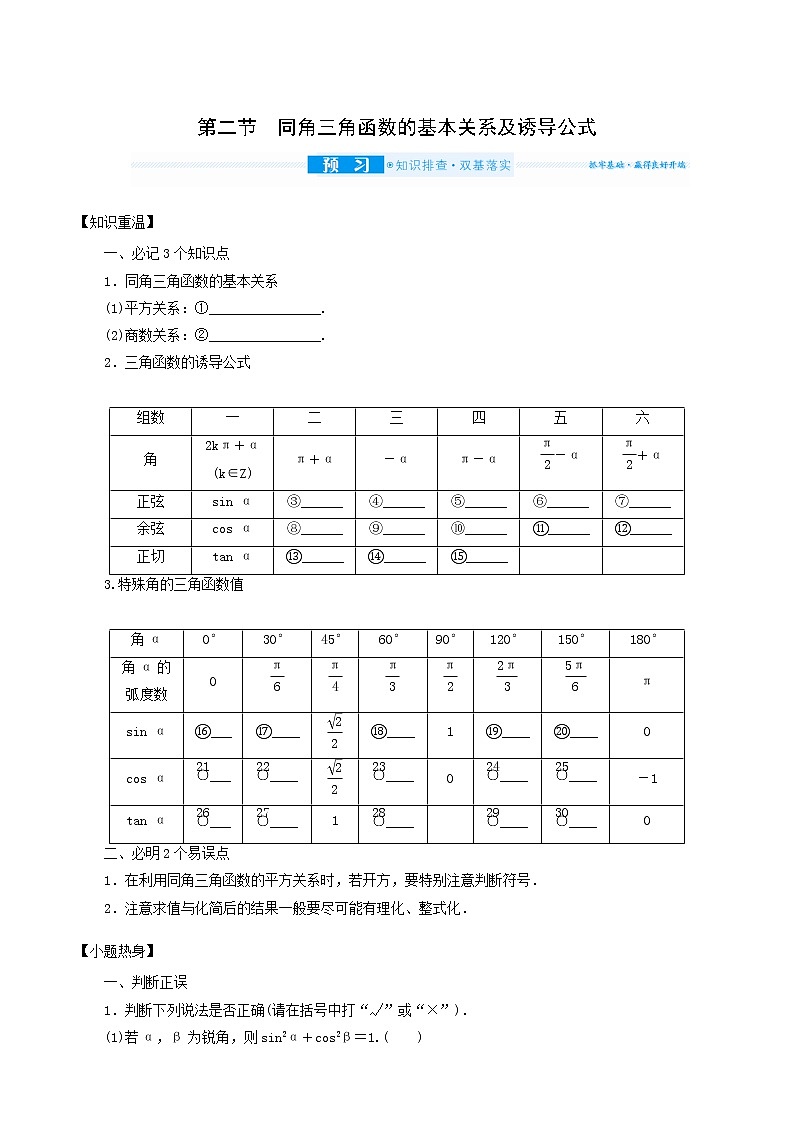
第二节　同角三角函数的基本关系及诱导公式【知识重温】一、必记3个知识点1．同角三角函数的基本关系(1)平方关系：①________________.(2)商数关系：②________________.2．三角函数的诱导公式 组数一二三四五六角2kπ＋α(k∈Z)π＋α－απ－α－α＋α正弦sin α③______④______⑤______⑥______⑦______余弦cos α⑧______⑨______⑩______⑪______⑫______正切tan α⑬______⑭______⑮______  3.特殊角的三角函数值 角α0°30°45°60°90°120°150°180°角α的弧度数0πsin α⑯___⑰____⑱____1⑲____⑳____0cos α___________0________－1tan α_______1____ ________0二、必明2个易误点1．在利用同角三角函数的平方关系时，若开方，要特别注意判断符号．2．注意求值与化简后的结果一般要尽可能有理化、整式化．【小题热身】一、判断正误1．判断下列说法是否正确(请在括号中打“√”或“×”)．(1)若α，β为锐角，则sin2α＋cos2β＝1.(　　)(2)若α∈R，则tan α＝恒成立．(　　)(3)sin(π＋α)＝－sin α成立的条件是α为锐角．(　　)二、教材改编2．已知sin(＋α)＝，则cos α＝(　　)A．－　　　B．－　　　C.　　　D.3．化简 －(α为第二象限角)＝______.　三、易错易混4．已知sin(π－α)＝－，且α∈(－，0)，则tan(2π－α)等于(　　)A.  B．－  C.  D．－5．已知sin α＋cos α＝－，且0<α<π，则tan α＝________.四、走进高考6．[2019·全国卷Ⅰ]tan 255°＝(　　)A．－2－  B．－2＋  C．2－  D．2＋   　三角函数的诱导公式[自主练透型]1．sin(－1 200°)cos 1 290°＝________.2．若f(x)＝sin＋1，且f(2 020)＝2，则f(2 021)＝________.3．[2021·合肥检测]在平面直角坐标系中，若角α 的终边经过点P，则sin(π＋α)＝(　　)A．－　　　B．－　　　C.　　　D.悟·技法1.利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤 2．利用诱导公式化简三角函数的要求(1)化简过程是恒等变形；(2)结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的求出值.考点二　同角三角函数关系式的应用[互动讲练型]考向一：公式的直接应用[例1]　(1)已知角α是第二象限角，且满足sin＋3cos(α－π)＝1，则tan(π＋α)等于(　　)A.　　　B．－　　　C．－　　　D．－1(2)[2021·北京市适应性测试]已知α是第四象限角，且tan α＝－，则sin α＝(　　)A．－  B.  C.  D．－ 悟·技法同角三角函数关系式的应用方法(1)利用sin2α＋cos2α＝1可实现α的正弦、余弦的互化，利用＝tan α可以实现角α的弦切互化．(2)由一个角的任意一个三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式，需求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论.考向二：已知tan α，求关于sin α与cos α的齐次式的值[例2]　(1)若tan θ＝3，则等于(　　)A．2  B．－2  C.  D．－(2)已知tan α＝2，则＝________.悟·技法已知角α的正切值，求由sin α和cos α构成的代数式的值，构成的代数式通常是分式齐次式或整式齐次式．(1)形如的分式，可将分子、分母同时除以cos α；形如的分式，可将分子、分母同时除以cos2α，将正、余弦转化为正切，从而求值．(2)形如asin2α＋bsin αcos α＋ccos2α的式子，可将其看成分母为1的分式，再将1变形为sin2α＋cos2α，转化为形如的分式求解. 考向三：利用sin θ±cos θ与sin θcos θ之间的关系求值[例3]　已知sin θ＋cos θ＝，0<θ<π，则sin θ－cos θ的值为________． 悟·技法在同角三角函数的基本关系中，sin2α＋cos2α＝1可变换成(sin α＋cos α)2－2sin αcos α＝1，其中sin α＋cos α与sin α·cos α很容易与一元二次方程的根与系数的关系产生联系．若以sin α，cos α为两根构造一元二次方程，则可利用上述关系解决相关问题．如本题中，易知sin θ，cos θ是关于x的方程x2－x－＝0的两个实数根，解方程可求出sin θ和cos θ.  考向四：三角函数式的化简[例4]　(1)；(2) ＋ (180°<α<270°)． 悟·技法同角三角函数式化简过程中常用的方法：(1)对于含有根号的，常把被开方数(式)去根号达到化简的目的；(2)化切为弦，从而减少函数名称，达到化简的目的；(3)对于含高次的三角函数式，往往借助于因式分解或构造sin2α＋cos2α＝1，以降低次数，达到化简的目的. [变式练]——(着眼于举一反三)1．已知α是第四象限角，sin α＝－，则tan α等于(　　)A．－  B.   C．－  D.2．已知tan α＝3，则sin·cos的值为(　　)A.     B．－  C.  D．－3．[2021·吉林部分名校3月联考]若sin θ－cos θ＝，且θ∈，则sin(π－θ)－cos(π－θ)＝(　　)A．－  B.  C．－  D.4．已知＝5，则cos2α＋sin αcos α的值是(　　)A.  B．－  C．－3  D．3     第二节　同角三角函数的基本关系及诱导公式 【知识重温】①sin2α＋cos2α＝1　②tan α＝　③－sin α　④－sin α　⑤sin α　⑥cos α　⑦cos α　⑧－cos α　⑨cos α　⑩－cos α　⑪sin α　⑫－sin α⑬tan α　⑭－tan α　⑮－tan α　⑯0　⑰⑱　⑲　⑳　1　　　－　－　0　　－　－【小题热身】1．答案：(1)×　(2)×　(3)×2．解析：∵sin(＋α)＝sin[2π＋π＋(＋α)]＝－sin(＋α)＝－cos α＝，∴cos α＝－，故选B.答案：B3．解析：∵α为第二象限角，∴原式＝－＝－＝－＋＝－2tan α.答案：－2tan α4．解析：∵sin(π－α)＝－，∴sin α＝－，又∵α∈(－，0)，∴cos α＝，则tan α＝－，∵tan(2π－α)＝－tan α，∴tan α＝.答案：A5．解析：∵0<α<π，∴sin α>0，又∵sin α＋cos α＝－，则cos α＝－－sin α代入cos2α＋sin2α＝1得sin α＝，cos α＝－，∴tan α＝－.答案：－6．解析：tan 255°＝tan(180°＋75°)＝tan 75°＝tan(45°＋30°)＝＝＝2＋.故选D.答案：D课堂考点突破考点一1．解析：原式＝－sin 1 200°cos 1 290°＝－sin(3×360°＋120°)cos(3×360°＋210°)＝－sin 120°cos 210°＝－sin(180°－60°)cos(180°＋30°)＝sin 60°cos 30°＝×＝.答案：2．解析：因为f(2 020)＝sin＋1＝sin(1 010π＋α)＋1＝sin α＋1＝2，所以sin α＝1，cos α＝0.所以f(2 021)＝sin＋1＝sin＋1＝cos α＋1＝1.答案：13．解析：因为sin＝－sin＝－，cos＝cos＝，所以点P为，角α的终边在第二象限，根据任意角的三角函数的定义可得sin α＝＝，所以sin(π＋α)＝－sin α＝－，选A.答案：A考点二例1　解析：(1)由sin＋3cos(α－π)＝1，得cos α－3cos α＝1，∴cos α＝－，∵角α是第二象限角，∴sin α＝，∴tan(π＋α)＝tan α＝＝－.(2)因为tan α＝＝－，所以cos α＝－ sin α　①，sin2α＋cos2α＝1　②，由①②得sin2α＝，又α是第四象限角，所以sin α<0，则sin α＝－，故选A.答案：(1)B　(2)A例2　解析：(1)因为tan θ＝3，所以＝＝＝2.(2)原式＝，又tan α＝2，∴原式＝＝.答案：(1)A　(2)例3　解析：∵sin θ＋cos θ＝，∴(sin θ＋cos θ)2＝，解得sin θcosθ＝－，∴(sin θ－cos θ)2＝1－2sin θcos θ＝，∵0<θ<π且sin θcos θ<0，∴sin θ>0，cos θ<0，∴sin θ－cos θ>0，∴sin θ－cos θ＝.答案：例4　解析：(1)原式＝＝＝＝－1.(2)原式＝ ＋＝＋＝.∵180°<α<270°，∴sin α<0，∴原式＝－.变式练1．解析：因为α是第四象限角，sin α＝－，所以cos α＝＝，故tan α＝＝－.答案：C2．解析：通解　依题意，sin·cos＝－cos αsin α＝＝＝－，故选B.优解　因为tan α＝3，所以sin α＝3cos α，又sin2α＋cos2α＝1，所以cos2α＝.而sin·cos＝－cos αsin α＝－3cos2α＝－.故选B.答案：B3．解析：由sin θ－cos θ＝得1－2sin θcos θ＝，即2sin θcos θ＝－，∴(sin θ＋cos θ)2＝1＋2sin θcos θ＝，又θ∈，∴sin θ＋cos θ<0，∴sin θ＋cos θ＝－，则sin(π－θ)－cos(π－θ)＝sin θ＋cos θ＝－，故选A.答案：A4．解析：因为＝5，所以＝5，解得tan α＝2，所以cos2α＋sin αcos α＝＝＝＝.答案：A